Метод минимальных поправок

Содержание

1. Введение. Постановка задачи..................................................................... 3

2. Описание методов решения задачи............................................................ 4

2.1 Метод минимальных невязок................................................................ 4

2.2. Метод минимальных поправок............................................................. 4

2.3. Метод скорейшего спуска.................................................................... 5

2.4. Метод сопряженных градиентов.......................................................... 5

3. Алгоритмы и блок-схемы решения............................................................. 8

3.1. Метод минимальных невязок............................................................... 8

3.2. Метод минимальных поправок............................................................. 9

3.3. Метод скорейшего спуска.................................................................. 10

3.4. Метод сопряженных градиентов......................................................... 11

4.Руководство пользователя......................................................................... 13

5. Тестирование и оптимизация................................................................... 15

6. Выводы.................................................................................................... 18

Список использованных источников........................................................... 19

Приложение 1. Контрольные примеры......................................................... 20

Приложение 2. Код программы.................................................................... 22

 

Введение. Постановка задачи.

Большое количество задач математики и физики сводится к решению дифференциальных уравнений в частных производных, решение которых, в свою очередь, приводит к решению систем линейных алгебраических уравнений (СЛАУ). Методы решения СЛАУ, можно разделить на прямые методы, позволяющие получить точное решение системы (к ним относится, например, метод Гаусса, метод Крамера и т. д.) и итерационные методы, позволяющие получить решение системы с заданным приближением. Среди итерационных методов особое место занимают методы вариационного типа, особенностью которых является то, что при их использовании нет необходимости знать границы спектра матрицы системы.

Итак, сформулируем задачу:

Дана система линейных уравнений

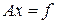
где A симметричная положительно определенная матрица.

Требуется решить данную СЛАУ следующими итерационными методами вариационного вида:

1. Метод минимальных невязок

2. Метод минимальных поправок

3. Метод скорейшего спуска

4. Метод сопряженных градиентов

 

Методы решения СЛАУ рассматриваются практически в каждой книге по численным методам. Общее описание алгоритмов для каждого метода дано, например, в книге Самарского А.А., Гулина А.В. «Численные методы» [3]. Также популярными книгами являются: М.Ю. Баландин, Э.П. Шурина “Методы решения СЛАУ большой размерности” [1], Y.Saad “Iterative Method for Sparse Linear System” [5]. В перечисленных книгах, описаны такие методы как CG (Conjugate Gradient – метод сопряжённых градиентов) и MinRES (Minimal Residual – метод минимальных невязок). В книге [5] изложены не только базовые алгоритмы данных методов, но и указания к их практической реализации.

Описание методов решения задачи

Метод минимальных невязок

Рассмотрим систему 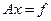с матрицей A = A^T >0. Обозначим через

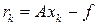(1)

невязку, которая получается при подстановке приближенного значения x_k, полученного на k -й итерации, в уравнение (1). Заметим, что погрешность z_k=x_k - х и невязка r_k связаны равенством Az_k=r_k.

Рассмотрим явный итерационный метод

, (2) <=> (3)

где параметр t _{k +l} выбирается из условия минимума погрешности || r_{k +1}|| при заданной норме || r_k ||.Метод (2) называется методом минимальных невязок.

Найдем явное выражение для параметра t _{k +l}. Из (3) получаем

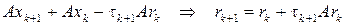, (4) => (5)

т. е. r_k удовлетворяет тому же уравнению, что и погрешность z_k=x_k - х. Возводя обе части уравнения (5) для невязки скалярно в квадрат, получаем

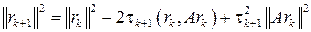(6)

Отсюда видно, что r_{k +1}|| достигает минимума, если

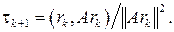(7)

Таким образом, в методе минимальных невязок переход от k -й итерации к (k +1)-й осуществляется следующим образом. По найденному значению x_k вычисляется вектор невязки r_k=Ax_k - f и по формуле (7) находится параметр t _{k +l}. Затем по формуле (3) досчитывается вектор x_{k+ 1}.

Метод минимальных невязок (3), (7) сходится с той же скоростью, что и метод простой итерации с оптимальным параметром t.

Метод минимальных поправок

Рассмотрим неявный итерационный метод вида

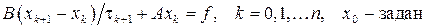, (8)

Запишем этот метод в виде

. (9)

Вектор w _k =B ^-1 r_k называется поправкой на (k +1)-й итерации. Она удовлетворяет тому же уравнению, что и погрешность z_k=x_k - x неявного метода, т. е.

уравнению

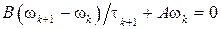. (10)

Будем предполагать, что B = B^T >0. Методом минимальных поправокназывается неявный итерационный метод (8), в котором параметр t _{k +l}выбирается из условия минимума нормы ||w _{k +1}|| _B =(B w _{k +1},w _{k +1})^1/2 при заданном векторе w _k. В случае B = Е метод минимальных поправок совпадает с методом минимальных невязок.

Найдем выражение для итерационного параметра t _{k +l}. Перепишем (10) в виде

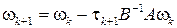
и вычислим

.

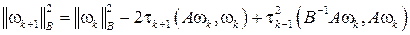Отсюда следует, что минимум этого выражения достигается при

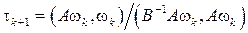. (11)

Для реализации метода минимальных поправок требуется на каждой итерации решить две системы уравнений B w _k= r_k и Bv_k=A w _k, откуда найдем вектор v_k = B ^-1 А w _k (воспользуемся формулой (9)).

Скорость сходимости метода минимальных поправок определя­ется границами спектра обобщенной задачи на собственные значения

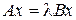. (12)

Метод скорейшего спуска

Рассмотрим явный метод (2) и выберем итерационный параметр t _{k +l} из условия минимума || z_{k +1}|| _A при заданном векторе z_k, где z_{k +1} =x_{k +1}- x. Поскольку погрешность z_k удовлетворяет уравнению

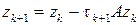, то

.

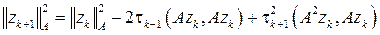Следовательно, это выражение достигает минимума, если

.

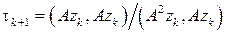Величина z_k=x_k - x здесь неизвестна (так как неизвестно точное решение х), поэтому надо учесть, что Az_k=r_k=Ax_k - f, и вычислять t _{k +l} по формуле

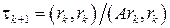. (13)