КУРСОВОЙ ПРОЕКТ (РАБОТА)
По дисциплине
«Расчет электрических цепей»
Вариант курсового проекта (работы): 44
Студент группы КУБ-1-11 Вязовецков В. С.
Руководитель курсового проекта (работы) Цыганов В.И.
Доцент, кандидат технических наук
Рецензент
Работа представлена к защите «__»_________201__г.
(подпись студента)
«Допущен к защите» «__»_________201__г.
(подпись руководителя)
МОСКВА 2012
Задание на выполнение Курсовой Работы
Основная часть
Задача 1.1. Линейные электрические цепи постоянного тока
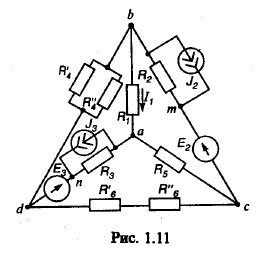 Рис.0. Схема 1 (общая)
Рис.0. Схема 1 (общая)
| Дано: R1=40 Ом R2=160 Ом R3=200 Ом R4”=120 Ом R4’=168 Ом R5=300 Ом R6’=40 Ом R6”=40 Ом | E1=0 В E2=200 В E3=800 В J2= 0 В J3=1,5 В | |
| 1. Преобразование общей схемы по варианту | |||
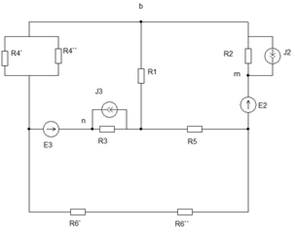 Рис.1. Схема 2 (частная по варианту) Переходим к квадратной схеме.
Рис.1. Схема 2 (частная по варианту) Переходим к квадратной схеме.
| 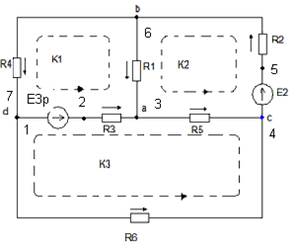 Рис.2. Схема 3(Расчётная). Выбор обхода контуров.
Рис.2. Схема 3(Расчётная). Выбор обхода контуров.
| ||
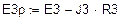
|
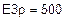
|
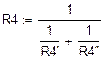
|
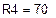
|
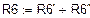
|
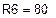
|
Расчет неизвестных токов в ветвях по законам Кирхгофа
б) Для схемы 3: Число неизвестных токов - 6, число узлов – 4, число уравнений по I закону Кирхгофа 4-1=3, число уравнений по II закону Кирхгофа 6-3=3. Контуры и направления обхода выбираем по схеме 3.
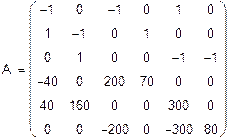
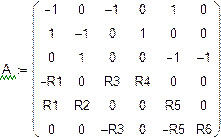
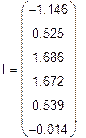
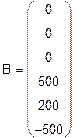
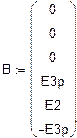
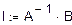
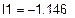
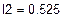
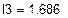
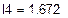
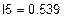
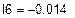
Расчет неизвестных токов в ветвях МКТ
Число уравнений системы МКТ равно число уравнений по II закону Кирхгофа. В контурах I, II, III протекают неизвестные контурные токи Ik 1, I k 2, I k 3, которые и являются неизвестными системы. В ветви с источником тока течет известный ток J 3, который создает в ячейке известный контурный ток J k 3 =J 3 =1,5 A (схема 3).
Составим систему(относительно Ik 1, I k 2, I k 3) и решим ёё матричным методом.
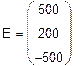 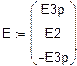
|
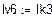
|
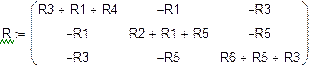
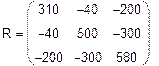
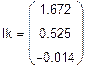
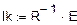
Решая систему относительно неизвестных, находим контурные токи 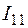 = 1,672 А,
= 1,672 А, 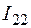 = 0,525 А,
= 0,525 А, 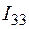 = -0.014 А и по принципу наложения выражаем через них токи в ветвях. Если контурный ток течет согласно с принятым направлением тока, то он берется со знаком плюс и наоборот.
= -0.014 А и по принципу наложения выражаем через них токи в ветвях. Если контурный ток течет согласно с принятым направлением тока, то он берется со знаком плюс и наоборот.
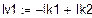
|
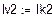
|
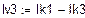
|
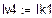
|
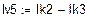
|
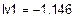
|
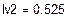
|
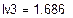
|
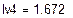
|
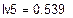
|
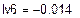
|
Расчет неизвестных токов в ветвях МУП
Число уравнений системы равно числу уравнений по I закону Кирхгофа. Неизвестными системы являются неизвестные потенциалы узлов. Потенциал одного из узлов примем равным 0. В схеме, где есть ветвь, содержащая только Е, нужно выбирать за нуль потенциал одного из узлов этой ветви.
Для схемы 3: 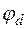 = 0
= 0
Неизвестными будут 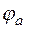 ,
, 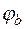 и
и 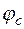 .
.
|
Составим систему(относительно 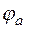 ,
, 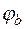 ,
, 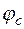 ) и решим ёё матричным методом.
) и решим ёё матричным методом.
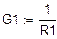
|
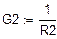
|
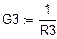
|
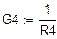
|
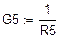
|
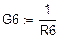
|
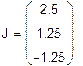
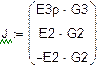
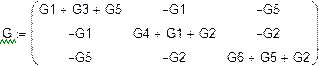
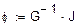
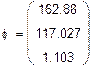
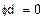
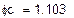
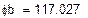
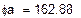
Решая систему относительно неизвестных, находим неизвестные потенциалы узлов:
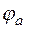 = 162,88 B
= 162,88 B 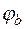 = 117,027
= 117,027 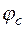 = 1,103 B
= 1,103 B
Выражаем токи в ветвях по закону Ома.
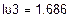 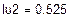
|
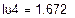
|
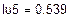
|
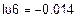
|
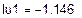
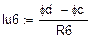
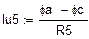

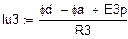
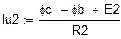
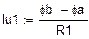
5. Сравнительная таблица результатов расчета токов *
 А А
|  А А
| 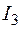 А А
| 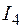 А А
| 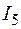 А А
| 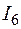 А А
| |||
| Кирхгоф | -1,146 | 0,525 | 1,686 | 1,672 | 0,539 | -0,014 | ||
| МКТ | -1,146 | 0,525 | 1,686 | 1,672 | 0,539 | -0,014 | ||
| МУП | -1,146 | 0,525 | 1,686 | 1,672 | 0,539 | -0,014 | ||
_________
* При сравнительных расчетах допустимая погрешность не должна превышать 5% от минимального значения величины.
Баланс мощностей (в схеме 3)
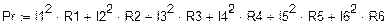
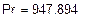
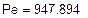
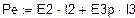
Проверка баланса:
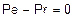
 7.Расчет I1 для схемы 2 МЭГ
7.Расчет I1 для схемы 2 МЭГ
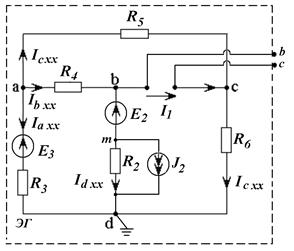
Примем 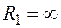 , т.е. рассмотрим схему 3 в режиме ХХ. Получим схему рис.6, соответствующую эквивалентному генератору. Это новая схема 4, в которой выбираем направления новых токов
, т.е. рассмотрим схему 3 в режиме ХХ. Получим схему рис.6, соответствующую эквивалентному генератору. Это новая схема 4, в которой выбираем направления новых токов 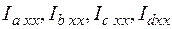 . У нее три узла a, m, d. Значит, МУП соответствует система2 уравнений. МКТ также соответствует
. У нее три узла a, m, d. Значит, МУП соответствует система2 уравнений. МКТ также соответствует
Рис. 6. Схема 4 система 2 уравнений (см. рис.7.),
т.к. в схеме 2 контура с неизвестными контурными токами 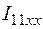 и
и 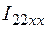 . (Схеме 3 будет соответствовать система: МКТ – 2 уравнения, МУП – 1 уравнение)
. (Схеме 3 будет соответствовать система: МКТ – 2 уравнения, МУП – 1 уравнение)
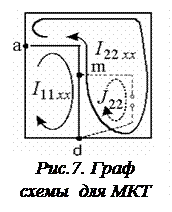 Ветвь с J 2 создает известный контурный ток J 22 =J 2 .
Ветвь с J 2 создает известный контурный ток J 22 =J 2 .
а) Система МУП: примем 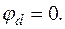 Рис.7.
Рис.7.
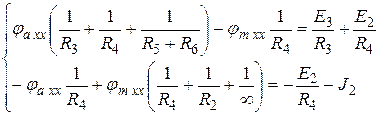
Матрица в числах:
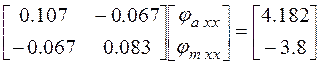
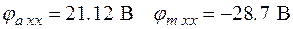
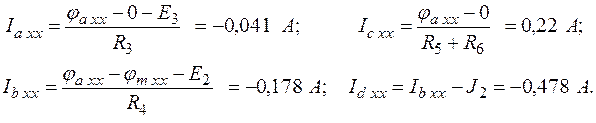
б) Система МКТ (рис.7):
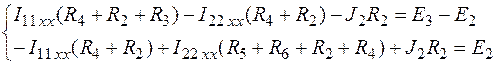
Перенесем в правую часть уравнения в цифрах J 2 R 2 и составим матричные уравнения.
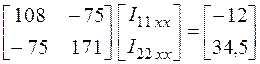
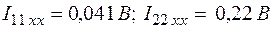
Выражаем токи в ветвях через контурные.
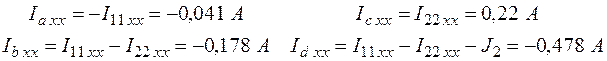 в) Сравним токи в ветвях, полученные МУП и МКТ.
в) Сравним токи в ветвях, полученные МУП и МКТ.
г) Находим 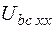 (т.к. ток
(т.к. ток 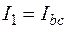 в схемах 2 и 3). Рассчитываем его по 2 различным путям, делая переход от второй точки «с» к первой «b». Изменение потенциалов на элементах учитываем по закону Ома (Рис. 6). Примем
в схемах 2 и 3). Рассчитываем его по 2 различным путям, делая переход от второй точки «с» к первой «b». Изменение потенциалов на элементах учитываем по закону Ома (Рис. 6). Примем  , тогда
, тогда
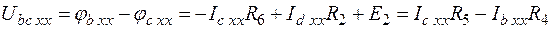
7,296 В =7,296 В.
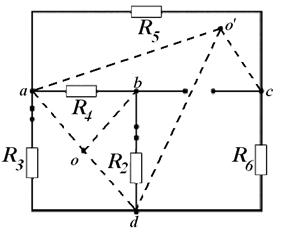 Рис. 8
Рис. 8
| д) Определим входное сопротивле-ние схемы 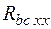 . Удаляем источники энергии, оставляя вместо источника э.д.с. . Удаляем источники энергии, оставляя вместо источника э.д.с. 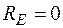 , и , и 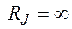 (обрыв), вместо (обрыв), вместо  . В схеме рис.8. нельзя выделить параллельные и последовательные участки, поэтому делаем преобразование треугольника abd в звезду (или acd). . В схеме рис.8. нельзя выделить параллельные и последовательные участки, поэтому делаем преобразование треугольника abd в звезду (или acd).
|
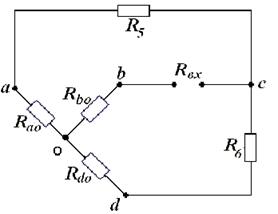 Рис.9.
Рис.9.
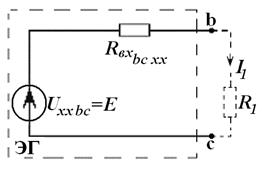 Рис.10.
Схема замещения для расчета I1 МЭГ
Рис.10.
Схема замещения для расчета I1 МЭГ
| 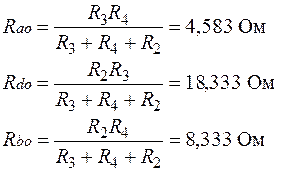
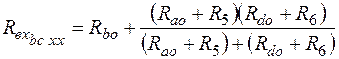
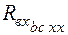 =28.412 Ом
(сравниваем результаты, полученные для ∆ abd и acd).
е) Определяем ток =28.412 Ом
(сравниваем результаты, полученные для ∆ abd и acd).
е) Определяем ток 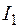 согласно схеме замещения (Рис. 10). согласно схеме замещения (Рис. 10). 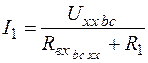 =0,099 A
Сравним =0,099 A
Сравним 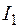 с таблицей (п.5). с таблицей (п.5).
|
8. Расчёт и построение потенциальной диаграммы
а) Одномерный массив потенциалов точек контура (начало – узел «d»)
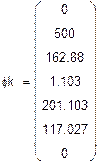
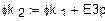
|
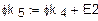
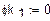
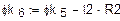
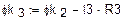
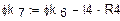
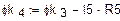
б) Одномерный массив сопротивлений вдоль пути контура
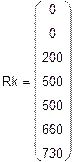
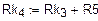
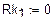
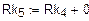
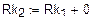
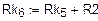
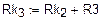
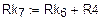
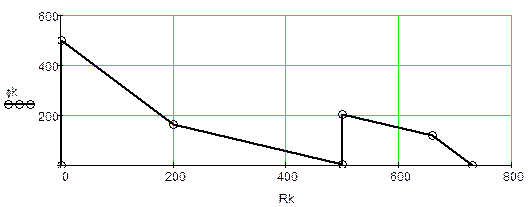
Потенциальная диаграмма
Заключение (Выводы)
Список использованных источников







