Министерство образования Российской Федерации
Уфимский государственный авиационный технический университет
 Кафедра Сопротивления материалов
Кафедра Сопротивления материалов
Расчёт на прочность, жёсткость и
Проектирование бруса в условиях
Сложного сопротивления
Статическому и динамическому нагружению
Курсовая работа по сопротивлению материалов.
| должность | Ф.И.О | дата | подпись | |
| Выполнил | ||||
| Проверил | ||||
| Принял |
Уфа 2007
 Содержание:
Содержание:
1. Напряжение и деформированное состояние в опасной точке, проверка прочности………………………………………………………………………3
1.1 Определение главных напряжений и проверка прочности………………….3
1.2 Проверка прочности…………………………………………………………..4
2. Компоненты тензора напряжений и проверка прочности в простейших
случаях сопротивления бруса…………………………………………………5
2.1 Расчет на прочность конструкций типа кронштейнов, подвесок, валов,
элементы которые работают на равномерное растяжение, сжатие………….5
2.1.1.Силовая задача…………………………………………………………..…...5
2.2. Расчет на прочность и жесткость конструкций типа валов, осей,
работающих на кручение……………………………………………………..8
3. Прочность и проектирование бруса, работающего при плоском
поперечном прямом изгибе…………………………………………………...13
3.1. Построение эпюры и расчет на прочность «оптимальной» балки с
составным поперечным сечением…………………………………………....13
3.2 Определение параметров поперечного сечения тонкостенной балки и
полная проверка прочности………………………………………………….16
Список литературы…………………………………………………………...23
 1. Напряженное и деформированное состояние в опасной точке, проверка прочности
1. Напряженное и деформированное состояние в опасной точке, проверка прочности
1.1. Определение главных напряжений в опасной точке и проверка

|
| σx, МПа | σy, МПа | σz, МПа | τxy, МПа | τzy, МПа | τxz, МПа |
| -310 |
|
|
|

|
|
|
|
Инварианты напряженного состояния по заданным компонентам
I1= σx +σy +σz=460
I2= σy ּ σz +σz ּ σx +σx ּ σy -τxy2 -τzy2 -τxz2= -224200

 σx τxy τxz
σx τxy τxz
I3= τxy σy τzy = (σx ּ σy ּ σz+ τxy ּ τzy ּ τxz+ τxy ּ τzy ּ τxz) - (τxz ּ σy ּ τxz+τxy ּ τxy ּ σz+τzy ּ τzy ּ σx)
τxz τzy σz =-85345000
Нахождение главных напряжений решением кубического уравнения
σk3 - σk2 ּ I1 + σk ּ I2 - I3 = 0
σk3 - σk2 ּ 460 - σk ּ 224200 - 85345000 = 0
Приводим уравнение к каноническому виду
q = 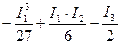 = 21878796,29
= 21878796,29
p =  = -98244,45
= -98244,45
r =  = 313,44 (т.к. q > 0)
= 313,44 (т.к. q > 0)
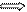
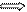
 =
=  = 0,7105
= 0,7105  = 44,72˚
= 44,72˚  = 14,9˚
= 14,9˚
y1 =  = -605,8
= -605,8
y2 =  = 442,49
= 442,49
y3 =  = 163,31
= 163,31
σ1 = 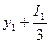 = -452,4
= -452,4
σ2 = 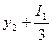 = 595,82
= 595,82
σ3 = 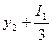 = 316,64
= 316,64
 σ1 >σ2 >σ3 σ1 = -452,4; σ2 = 595,82; σ3 = 316,64
σ1 >σ2 >σ3 σ1 = -452,4; σ2 = 595,82; σ3 = 316,64
Проверка
I1г = σ1 + σ2 + σ3 = 460
I2г = σ1 ּ σ2 +σ1 ּ σ3 +σ2 ּ σ3 = -224200
I3г = σ1 ּ σ2 ּ σ3 = -85345000
ΔI1= (I1г- I1)/ I1=0
ΔI2= (I2г- I2)/ I2=0
ΔI3= (I3г- I3)/ I3=0
 1.2. Проверка прочности
1.2. Проверка прочности
Условие прочности: n > [n] n = 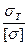 [n] =
[n] = 
Материал 12ХН3А
σТ =700 МПа
σВ =950 МПа
[n] =  = 1,74
= 1,74
n = 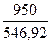 = 1,279
= 1,279
 n < [n] условие прочности не выполняется.
n < [n] условие прочности не выполняется.
2. Компоненты тензора напряжений и проверка прочности в простейших случаях сопротивления бруса
Расчет на прочность конструкций типа кронштейнов, подвесок, валов, элементы которых работают на равномерное растяжение, сжатие.
Силовая задача

 l1 = l2 = 24 см
l1 = l2 = 24 см
l3 = l4=31 см
A1 = A2 = 2,5 см2
A3 = A4 = 2 см2
F= 120 КН
α1=53°
α2=40°
Материал – 12ХНЗА

Определение статической неопределимости

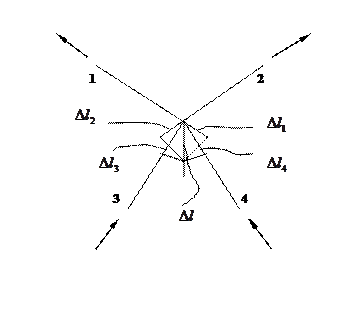







Уравнение деформации
Используя закон Гука имеем:
 ;
;
 ;
; 



2.1.4 Определение внутренних усилий
 ;
;
 ;
;
 ;
;
 ;
;
N4=313,3 кН;
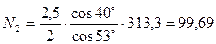 кН
кН
N1=N2 = 99,69 кН
N3=N4 = 313,3 кН.
 2.1.5 Нахождение напряжений в стержнях
2.1.5 Нахождение напряжений в стержнях

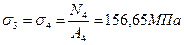
Проверка прочности
Условие прочности: n>[n] n=  [n] =
[n] = 
[n] =  = 1,74
= 1,74
n =  = 4,47 МПа
= 4,47 МПа
 n > [n] условие прочности выполняется
n > [n] условие прочности выполняется
 2.2 Расчет на прочность и жесткость конструкций типа валов, осей, работающих на кручение
2.2 Расчет на прочность и жесткость конструкций типа валов, осей, работающих на кручение

M1 = -30 кН·м
M2 = -25 кН·м
M3 = 10 кН·м
КD1 = 6.5
КD2 = 6.0
КD3 = 2,5
Кd1 = 5.5
Кd2 = 5.5
Кd3 = 2.0
l1 = 0,65м; l2 = 0,5м; l3 = 0,45м
Материал – Ст.45;  = 360МПа;
= 360МПа;  = 610 МПа; G = 80 ГПа
= 610 МПа; G = 80 ГПа
Определение величины реактивного погонного момента
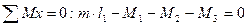 ; m
; m  = -69,23 кН·м
= -69,23 кН·м






