Простейшие случаи парной нелинейной корреляционной зависимости - это гиперболическая и параболическая зависимости. Их уравнения регрессии, соответственно, имеют следующий вид:
.
Как и в случае линейной зависимости, параметры ai, i = 0, 1, 2 находятся методом наименьших квадратов, который дает приведенные ниже системы нормальных уравнений.
Для гиперболической зависимости:
Для параболической зависимости:
Параметры ai находим, решая данные системы нормальных уравнений.
Прежде чем находить уравнение регрессии, необходимо оценить тесноту взаимосвязи между признаками и проверить значимость этой взаимосвязи.
Теснота взаимосвязи между признаками в нелинейной зависимости измеряется с помощью корреляционного отношения 
, рассчитываемого по формуле
где D общ - общая дисперсия признака Y;
D м/гр - межгрупповая дисперсия признака Y.
Можно показать, что общая дисперсия результативного признака Y складывается из двух дисперсий: межгрупповой и внутригрупповой, то есть D общ = D м/гр + D вн/гр,
Межгрупповая дисперсия D м/гр характеризует вариацию признака Y за счет учтенного фактора, а внутригрупповая дисперсия D вн/гр - за счет неучтенных факторов.
D общ = 
; D м/гр = 
;
D в/гр = 
, j = 
,
где yi - значение признака Y, i = 
;
- условнаясредняя признака Y, j = ;
- общая средняя признака Y;
- частота значений признака Y;
- частота значений признака X;
n - объем выборки (сумма всех частот).
Отметим основные свойства корреляционного отношения.
1. Корреляционное отношение изменяется от 0 до 1, то есть
.
Доказательство. Так как для вычисления следует извлечь арифметический квадратный корень из отношения 
, то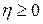 
. Так как 
, то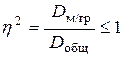 
. Следовательно, 
.
2. Если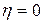 
, то корреляционная зависимость между признаками Х и Y отсутствует.
Доказательство. Если 
, то 
. Тогда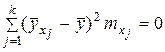 
. Следовательно, 
, где j=1,2,…,k. Поэтому с ростом значений признака X условные средние признака Y не меняются. А это и означает, что между признаками отсутствует корреляционная зависимость.
3. Если 
, то между факторами X и Y существует функциональная зависимость.
4. Корреляционное отношение связано с выборочным коэффициентом корреляции 
следующим неравенством:
.
5. Если корреляционная зависимость между признаками X и Y линейная, то 
.
Доказательство. Так как связь между признаками предполагается линейной, то ее можно описать с помощью линейного регрессионного уравнения: 
, где 
.
Тогда
Так как 
, то выражение для межгрупповой дисперсии примет вид D м/гр = 
.
Поэтому 
, что и требовалось доказать.
Замечание. Так как корреляционное отношение 
вычисляется по значениям переменных, случайно попавшим в выборку, то величина меняется от выборки к выборке. Следовательно, корреляционное отношение - величина случайная. Поэтому является оценкой генерального корреляционного отношения 
.
Проверка значимости корреляционного отношения h основана на том, что статистика (критерий) 
имеет распределение Фишера - Снедекора с 
и 
степенями свободы. Здесь 
- число различных значений дискретного признака X или число частичных интервалов изменения значений непрерывного признака X в выборке.
Выберем уровень значимости 
. В качестве нулевой гипотезы следует выдвинуть гипотезу H0: 
, то есть корреляционное отношение h, найденное по выборке, незначимо. В качестве конкурирующей гипотезы следует выдвинуть гипотезу
H1: 
, то есть h, найденное по выборке, значимо. По виду гипотезы H1 строится правосторонняя критическая область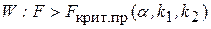 
.
Пример 4. Распределение 100 заводов по производственным средствам (Х, тыс. р.) и по суточной выработке (Y, т) дается в следующей корреляционной таблице:
| Х | Y | 
| |||||
|
Оценить тесноту взаимосвязи между производственными затратами и суточной выработкой при уровне значимости =0,05.
Решение. Признак Y - суточная выработка, т; признак Х - производственные затраты, тыс. р.
Признаки находятся в статистической зависимости. Тесноту взаимосвязи оценим с помощью корреляционного отношения: 
, где D общ = и D м/гр = .
Найдем групповые средние и общую среднюю признака Y.
общ 
Расчеты D м/гр и D общ представим в таблице:
| yi |
| (yi - )2
|
|
| ( - )2
|
| 2939,07 4990,59 2043,04 42,25 2270,7 5245,35 | 17,5 24,375 45,26 45,0 52,86 - | - | 2265,76 4583,290 893,8512 219,04 935,4352 - | ||
| Итого | - | 8897,3764 |
D м/гр = 
;
D общ = 
.
.
Проверим значимость полученного выборочного корреляционного отношения h при =0,05. Для этого выдвинем гипотезы 
и 
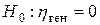. По виду гипотезы H1 строим правостороннюю критическую область 
.
Воспользуемся статистикой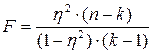 
, которая имеет распределение Фишера - Снедекора со степенями свободы и . Здесь 
- объем выборки, - число различных значений дискретного признака X в выборке, то есть = 100, = 5. Найдем наблюдаемое значение 
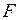-критерия:
.
Найдем критическое значение 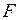-критерия по таблице критических точек распределения Фишера - Снедекора при уровне значимости =0,05 и числах степеней свободы 
и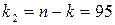 
: 
.
Так как наблюдаемое значение критерия попало в критическую область (
), то нулевая гипотеза отвергается, имеет место гипотеза , иными словами, выборочное корреляционное отношение значимо.
Легко проверить, что выборочный линейный коэффициент корреляции для данных наблюдения =0,59. Так как 
, то корреляционная зависимость между признаками X и Y нелинейная.
Пример 5. Размер производительности горных комбайнов (размер добычи на один выход) в зависимости от длины лавы характеризуется следующими данными:
| Х | |||||||||||
| Y | 1,74 | 2,02 | 2,12 | 2,05 | 2,17 | 2,74 | 2,40 | 2,48 | 2,50 | 2,39 | . |
Сгруппировав данные по длине лавы в границах (55; 95) и (105; 145), оценить тесноту взаимосвязи параболической зависимости и составить уравнение регрессии.
Решение. Признак Х - длина лавы; признак Y - производительность горного комбайна. Предполагается, что признаки имеют нормальное распределение. Они находятся в статистической зависимости, по условию задачи известно, что они связаны параболической зависимостью.
Предварительно оценим тесноту взаимосвязи между ними, вычислив корреляционное отношение 
.
Расчеты представим в таблице:
| х О (55;95) | х О (105;145) | |||
| yi | 
| yi |
| |
| 1,74 2,02 2,12 2,05 2,17 | 3,0276 4,0804 4,4944 4,2025 4,7089 | 2,74 2,40 2,48 2,50 2,39 | 7,5076 5,76 6,1504 6,25 5,7121 | |
| Итого | 10,1 | 20,5138 | 12,51 | 31,3801 |
общ = 
;
D общ = 
общ - 
= 5,1894 - (2,26)2 = 0,0818;
D м/гр = 
;
.
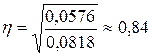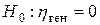Проверим значимость полученного выборочного корреляционного отношения h при =0,15. Для этого выдвинем гипотезы и . По виду гипотезы H1 строим правостороннюю критическую область 
.
Воспользуемся статистикой 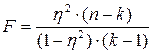, которая имеет распределение Фишера - Снедекора со степенями свободы и . Здесь 
- объем выборки, - число частичных интервалов изменения значений непрерывного признака X в выборке, то есть = 10,
= 2.
Найдем наблюдаемое значение 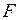-критерия:
.
Найдем критическое значение 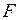-критерия по таблице критических точек распределения Фишера - Снедекора при уровне значимости =0,05 и числам степеней свободы 
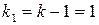и 
: 
.
Так как наблюдаемое значение критерия попало в критическую область (), то нулевая гипотеза отвергается, имеет место гипотеза , иными словами, выборочное корреляционное отношение значимо, и признаки X и Y связаны нелинейной (параболической) зависимостью.
Связь тесная, представим ее аналитически в виде уравнения регрессии вида х» a 0 + a 1 х + a 2 х 2. Параметры ai (i = 0,1,2) найдем из системы нормальных уравнений
Расчеты представим в таблице:
| хi | 
| 
| 
| yi | yixi | yi
|
| 1,74 2,02 2,12 2,05 2,17 2,74 2,40 2,48 2,50 2,39 | 95,7 131,3 174,25 206,15 287,7 337,5 346,55 | 5263,5 8534,5 11925 14811,25 19584,25 30208,5 45562,5 50249,75 | ||||
| Итого 1000 | 22,61 | 2324,15 | 256629,25 |
= 2,261; 
= 232,415; 
= 25662,925.
Система нормальных уравнений примет вид
Решая систему, получим: a 0» 0,185, a 1» 0,0362, a 2 » - 0,0001. Итак, уравнение регрессии имеет вид
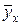» 0,185 + 0,0362 x - 0,0001 x 2.
Из приведенных громоздких расчетов следует необходимость использования ЭВМ. Ниже приведено решение этой же задачи на ЭВМ.
