Пусть даны признаки Х и У, которыми обладают элементы генеральной совокупности. Предполагаем, что они имеют совместное нормальное распределение. Чтобы изучить взаимосвязь между признаками, проведем выборку объемом n из двухмерной генеральной совокупности. В результате получим эмпирические данные:
| хi | х1 | х2 | ... | хn | |
| yi | y1 | y2 | ... | yn | . |
Построим точки с координатами (хi, уi), или корреляционное поле (рис. 4). Пусть по расположению построенных точек видно, что зависимость между X и Y близка к линейной: у=а0+а1х. Построим график этой зависимости.
Рис. 4
Эмпирические значения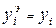 
соответствуют ординатам точек корреляционного поля на рис. 4; теоретические (расчетные) значения признака У найдены по уравнению 
и соответствуют ординатам точек с абсциссами хi, лежащих на прямой. На рис. 4 также показаны отклонения 
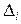эмпирических значений признака 
от расчетных 
. Обобщаемым показателем рассеяния эмпирических точек вокруг прямой будет сумма квадратов отклонений 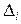, то есть
.
Чем меньше величина S, тем лучше прямая 
"подогнана" к точкам (хi, уi) корреляционного поля.
Необходимым условием существования минимума функции 
является равенство нулю одновременно всех ее частных производных.
Воспользуемся этим условием и получим следующую систему уравнений:
или 
Преобразуем эту систему:
Полученную систему еще можно упростить, поделив обе части каждого уравнения на n. Система примет следующий вид:
Эту систему называют системой нормальных уравнений. Система нормальных уравнений состоит из двух линейных уравнений с двумя неизвестными а 0, а 1.
Решая эту систему, например, методом Крамера, находим а 0, а 1.
, 
, 
Коэффициент а 1 называют коэффициентом регрессии у на х.
Коэффициенты а 0, а 1, вычисленные из системы нормальных уравнений, являются оценками истинных значений параметров регрессии.
Полученное уравнение регрессии 
называют эмпирическим уравнением регрессии. Преобразуем его. Подставим в это уравнение значение 
из первого уравнения системы нормальных уравнений:
или 
Уравнение регрессии в этой форме часто применяется на практике. Из данного уравнения мы можем выявить экономический смысл параметра а 1, который показывает, как изменяется в среднем результативный признак У, если факторный признак Х увеличится на единицу своего измерения.
Таким образом, по уравнению регрессии мы можем выяснить, как изменяется в среднем результативный признак (У) с изменением факторного признака (Х). Кроме того, уравнение регрессии приближенно выражает в виде функции корреляционную зависимость между признаками, и по нему можно прогнозировать значения результативного признака.
Корреляционный анализ
