X4≤20 – количество шкафов книжных.

Критерий эффективности

Цель задачи: Определить, какое количество изделий, выпускаемых фабрикой, удовлетворяющих последней системе, будет максимизировать прибыль.

Т.к. Прибыль от реализации единицы изделия – 60, 25, 140 и 160 р. соответственно организации операции и параметров, заданных выше, то целевая функция имеет вид: L(x) = 60x₁+25x₂ +140x₃+160x₄ (→max)

Стратегии ОС

Стратегиями оперирующей стороны в данной операции называются допустимые способы расходования ею имеющихся активных средств. В виду поставленной цели и имеющихся у меня в настоящий момент знаний, лучшая и выполнимая стратегия – рассчет оптимального количества изделий. ЛПР может перейти к другим стратегиям, путем введения новых ограничений, и активных средств. Так же можно предположить существование субъективных желаний исполнителя и заказчика, определяющее выбор стратегии ОС. Количество этих стратегий определяется многоугольником решений задачи. ЛПР может принять и выбрать любую из них.

3. Методы решения

Данная задача относится к типу целочисленных.

Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования.

Математическая модель целочисленной задачи:

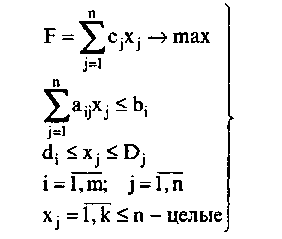
При решении полностью целочисленных задач линейного программирования используются:

- методы отсечений

- методы разветвлений

- приближенные методы (даны допустимые решения, хотя и в общем случае неоптимальные)

Небольшая размерность задачи позволяет применить метод динамического программирования и метод сечения Гомори. Т.к. в основе последнего лежит двойственный симплекс метод линейного программирования, позволяющий наряду с нахождением решения, выявить и чувствительность модели к изменению параметров, то решим задачу этим методом.

 

 

4. Решение задачи

Прежде чем приступить к решению задачи запишем ее в общем виде:

L

Максимизировать

при условиях

при .

Цель задачи – получение максимальной прибыли – может быть достигнута несколькими способами. Математическим выражением цели является критериальная функции L, структура которой отражает вклад каждого из способов достижения цели. В сформулированной задаче представлено n таких способов. Под способом достижения цели понимается получение информации о распределении ресурсов для максимизации прибыли. Коэффициент C_j представляет собой удельную прибыль применения j-того способа достижения цели (прибыль от продажи одного изделия j-того типа). Переменные Х_j – искомые величины, представляющие собой интенсивность использования j-того способа достижения цели (количество изделий j-того типа).

Для достижения цели имеем: m- виды ресурсов, b_i – возможный объем потребления i-того ресурса (максимальное количество древесного ресурса и трудового фактора). Коэффициент a_ij – расход

i-того ресурса для производства одного изделия j-того типа.

 

 

Метод Гомори

Решим задачу с нецелочисленными переменными:

Максимизировать

L(x) = 60x₁+25x₂ +140x₃+160x₄

при ограничениях

5x₁ + x₂ + 12x₃ + 15x₄≤1500

3x₁ + 2x₂ + 6x₃ + 5x₄≤1000

7x₁ + 5x₂ + 10x₃ + 12x₄≤3200

x₁≥40

x₂≥120

x₃≥20

x₄≤20

хi≥0

 

Этап 1

Приведем модель к стандартному виду: введем балансовые переменные x₅, x₆, x₇, x₈, x₉, x_10, x_{11 ,} не имеющие физического смысла для приведения неравенств к равенствам.

Максимизировать

L(x) = 60x₁+25x₂ +140x₃+160x₄

при ограничениях

5x₁ + x₂ + 12x₃ + 15x₄ + x₅ = 1500

3x₁ + 2x₂ + 6x₃ + 5x₄ + x₆ = 1000

7x₁ + 5x₂ + 10x₃ + 12x₄+x₇ = 3200

x₁ -x₈ = 40

x₂ -x₉ = 120

x₃-x₁₀ = 20

x₄ +x₁₁ = 20

X1… x11≥0

 

Решение системы производится путём ввода искусственных переменных Х_i. Для исключения из базиса этих переменных, их вводят в целевую функцию с большими отрицательными коэффициентами M, имеющими смысл "штрафов" за ввод искусственных переменных. Таким образом, из исходной получается новая M-задача.

Если в оптимальном решении М-задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении M-задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.

Симплекс-таблица, которая составляется в процессе решения, используя метод искусственного базиса, называется расширенной. Она отличается от обычной тем, что содержит две строки для функции цели: одна – для составляющей L(x), а другая – для составляющей M. При составлении симплекс таблицы полагают, что исходные переменные являются небазисными, а дополнительные (x_n+m) и искусственные (X_i)- базисными.

Этап 2

Введем искусственные переменные x₁₂, x₁₃, x₁₄

5x₁ + x₂ + 12x₃ + 15x₄ + x₅ = 1500

3x₁ + 2x₂ + 6x₃ + 5x₄+x₆ = 1000

7x₁ + 5x₂ + 10x₃ + 12x₄ +x₇ = 3200

x₁ -x₈ +x₁₂ = 40

x₂ -x₉ + x₁₃ = 120

x₃ -x₁₀ + x₁₄ = 20

x₄ +x₁₁ = 20

Целевая функция:

L(X) = 60x₁+25x₂+140x₃+160x₄ - Mx₁₂ - Mx₁₃ - Mx₁₄ → max

Из уравнений выражаем искусственные переменные:

x₁₂ = 40-x₁+x₈

x₁₃ = 120-x₂+x₉

x₁₄ = 20-x₃+x₁₀

подставим в целевую функцию:

L(X) = (60+M)x₁+(25+M)x₂+(140+M)x₃+(160)x₄+(-M)x₈+(-M)x₉+(-M)x₁₀+

+(-180M) x₁₁

Этап 3

Прежде чем приступить к симплекс-преобразованиям, запишем исходные данные:

1.Размерность матрицы А – m x n, m=7, n=14.

2.Матрица А:

-1

-1

-1

3.Вектор свободных членов в уравнениях ограничений b_i, i=1…m:

b=(1500,1000,3200,40,120,20,20)

4.Коэффициенты при переменных в критериальной функции C_j:

C=(60+M, 25+M, 140+M,160,0,0,0,-M,-M,-M, -180M,0,0,0)

Этап 4

Симплекс преобразования.

Решим систему уравнений относительно базисных переменных:

x₅, x₆, x₇, x₁₂, x₁₃, x₁₄, x₁₁,

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,0,0,1500,1000,3200,0,0,0,20,40,120,20)

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x5

x6

x7

x12

-1

x13

-1

x14

-1

x11

L(X0)

-180M

-60-M

-25-M

-140-M

-160

M

М

M

Итерация №0.

Первый опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец x₃, так как это наибольший коэффициент по модулю. Вычислим значения Ѳ по строкам как частное от деления:

b_i / a_i3 и из них выберем наименьшее: x₁₄ - разрешающая строка

Разрешающий элемент = 1.

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x5

x6

1662/3

x7

x12

-1

-

x13

-1

-

x14

-1

x11

-

L(X1)

-180M

-60-M

-25-M

-140-M

-160

M

M

M

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x5

-12

x6

-6

x7

-10

x12

-1

x13

-1

x3

-1

x11

L(X1)

2800-160M

-60-M

-25-M

-160

M

M

-140

140+M

 

Итерация №1.

Данный опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец x₁, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее: строка x₁₂

Разрешающий элемент = 1

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x5

-12

x6

-6

2931/3

x7

-10

4284/7

x12

-1

x13

-1

-

x3

-1

-

x11

-

L(X2)

2800-160M

-60-M

-25-M

-160

M

M

-140

140+M

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x5

-5

-12

x6

-3

-6

x7

-7

-10

x1

-1

x13

-1

x3

-1

x11

L(X2)

5200-120M

-25-M

-160

-60

M

-140

60+M

140+M

 

Итерация №2.

Текущий план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее: x₁₃ строка является разрешающей.

Разрешающий элемент =1

 

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x5

-5

-12

x6

-3

-6

x7

-7

-10

x1

-1

-

x13

-1

x3

-1

-

x11

-

L(X3)

5200-120M

-25-M

-160

-60

M

-140

60+M

140+M

 

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x5

-5

-1

-12

x6

-3

-2

-6

x7

-7

-5

-10

x1

-1

x2

-1

x3

-1

x11

L(X3)

-160

-60

-25

-140

60+M

25+M

140+M

 

Итерация №3.

Текущий опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец x₄, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i4

и из них выберем наименьшее: строка x₁₁

Разрешающий элемент =1.

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x5

-5

-1

-12

622/3

x6

-3

-2

-6

x7

-7

-5

-10

1762/3

x1

-1

-

x2

-1

-

x3

-1

-

x11

L(X4)

-160

-60

-25

-140

60+M

25+M

140+M

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14
x5												-15	-5	-1	-12
x6												-5	-3	-2	-6
x7												-12	-7	-5	-10
x1									-1
x2										-1
x3											-1
x4
L(X4)									-60	-25	-140		60+M	25+M	140+M

 

 

Итерация №4.

Текущий опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец x₁₀, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i10

и из них выберем наименьшее: строка x₅ разрешающая.

Разрешающий элемент =12.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	Ѳ
x5												-15	-5	-1	-12	531/3
x6												-5	-3	-2	-6
x7												-12	-7	-5	-10
x1									-1							-
x2										-1						-
x3											-1					-
x4																-
L(X5)									-60	-25	-140		60+M	25+M	140+M

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x10

531/3

1/12

5/12

1/12

-11/4

-5/12

-1/12

-1

x6

-1/2

1/2

11/2

21/2

-1/2

-11/2

x7

13462/3

-5/6

25/6

41/6

1/2

-25/6

-41/6

x1

-1

x2

-1

x3

731/3

1/12

5/12

1/12

-11/4

-5/12

-1/12

x4

L(X5)

188662/3

112/3

-12/3

-131/3

-15

12/3+M

131/3+M

M

 

Итерация №5.

Текущий опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец переменной x₁₁, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i11

и из них выберем наименьшее: x₄ разрешающая строка.

Разрешающий элемент = 1.

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x10

531/3

1/12

5/12

1/12

-11/4

-5/12

-1/12

-1

-

x6

-1/2

1/2

11/2

21/2

-1/2

-11/2

x7

13462/3

-5/6

25/6

41/6

1/2

-25/6

-41/6

26931/3

x1

-1

-

x2

-1

-

x3

731/3

1/12

5/12

1/12

-11/4

-5/12

-1/12

-

x4

L(X6)

188662/3

112/3

-12/3

-131/3

-15

12/3+M

131/3+M

M

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x10

781/3

11/4

1/12

5/12

1/12

-5/12

-1/12

-1

x6

-21/2

-1/2

1/2

11/2

-1/2

-11/2

x7

13362/3

-1/2

-5/6

25/6

41/6

-25/6

-41/6

x1

-1

x2

-1

x3

981/3

11/4

1/12

5/12

1/12

-5/12

-1/12

x11

L(X6)

191662/3

112/3

-12/3

-131/3

12/3+M

131/3+M

M

 

Итерация №6.

Текущий опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты.

В качестве разрешающего выберем столбец x₉, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i9

и из них выберем наименьшее: строка x₆ разрешающая.

Разрешающий элемент равен =1¹/₂

 

 

 

 

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x10

781/3

11/4

1/12

5/12

1/12

-5/12

-1/12

-1

x6

-21/2

-1/2

1/2

11/2

-1/2

-11/2

331/3

x7

13362/3

-1/2

-5/6

25/6

41/6

-25/6

-41/6

3204/5

x1

-1

-

x2

-1

-

x3

981/3

11/4

1/12

5/12

1/12

-5/12

-1/12

x11

-

L(X7)

191662/3

112/3

-12/3

-131/3

12/3+M

131/3+M

M

Получаем новую симплекс-таблицу:

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

x10

755/9

17/18

1/9

-1/18

7/18

-7/18

-1

x9

331/3

-12/3

-1/3

2/3

1/3

-1/3

-1

x7

11977/9

64/9

5/9

-27/9

14/9

-14/9

x1

-1

x2

1531/3

-12/3

-1/3

2/3

1/3

-1/3

x3

955/9

17/18

1/9

-1/18

7/18

-7/18

x11

L(X7)

196111/9

-72/9

72/9

88/9

27/9

-27/9+M

M

M

 

Итерация №7.

Текущий опорный план неоптимален, т.к. нарушены условия оптимальности: критериальная функция имеет отрицательные коэффициенты. В качестве разрешающего выберем столбец x₄, так как это наибольший коэффициент по модулю.

Вычислим значения Ѳ по строкам как частное от деления: b_i / a_i4

и из них выберем наименьшее: строка x₁₁ разрешающая.

Разрешающий элемент равен =1.

Базис

B

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

x13

x14

Ѳ

x10

755/9

17/18

1/9

-1/18

7/18

-7/18

-1

542/5

x9

331/3

-12/3

-1/3

2/3

1/3

-1/3

-1

-

x7

11977/9

64/9

5/9

-27/9

14/9

-14/9

18525/29

x1

-1

-

x2

1531/3

-12/3

-1/3

2/3

1/3

-1/3

-

x3

955/9

17/18

1/9

-1/18

7/18

-7/18

684/5

x11

L(X8)

196111/9

-72/9

72/9

88/9

27/9

-27/9+M

M

M

 

Получаем новую симплекс-таблицу:

Базис

B

x1

x2< ⇐ Предыдущая12 Поделиться с друзьями: Дата добавления: 2016-11-12; Мы поможем в написании ваших работ!; просмотров: 523 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: Есть только один способ избежать критики: ничего не делайте, ничего не говорите и будьте никем. © Аристотель ==> читать все изречения... 2217 - | 2173 - © 2015-2024 lektsii.org - Контакты - Последнее добавление

Ген: 0.014 с.