Ненулевой вектор 
называется собственным вектором линейного оператора 
, если 
(
для комплексного 
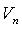), такое, что 
Число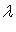 
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор 
имеет координатный столбец X, то 
или 
Собственные числа 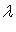линейного оператора - корни характеристического уравнения 
, где 
- матрица оператора f, 
- символ Кронекера.
Для каждого собственного значения 
соответствующие собственные векторы могут быть найдены из матричного уравнения 
или соответствующей ему системы линейных уравнений
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
где 
- соответствующие собственные значения.
№29
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:
(x, y) = (y, x),
(α ·x, y) = α ·(x, y),
(x + y, z) = (x, z) + (y, z),
(x, x) > 0 при x ≠ 0, (0, 0) = 0,
то в пространстве L определено скалярное произведение (x, y).
Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.
Норма вектора
Норма в векторном пространстве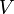 
над полем вещественных или комплексных чисел — это функционал 
, обладающий следующими свойствами:
1. 
2. 
(неравенство треугольника);
3. 
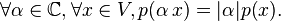
Эти условия являются аксиомами нормы.
Векторное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.
Нетрудно видеть, что из аксиом нормы вытекает свойство неотрицательности нормы:
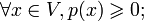
Действительно:
Из 3 получаем, что 
. Теперь из 2 получаем 
. Таким образом, 
.
Чаще всего норму обозначают в виде: 
. В частности,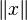 
— это норма элемента 
векторного пространства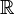 
.
Вектор с единичной нормой (
) называется нормальным или нормированным.
Любой ненулевой вектор можно нормировать, то есть разделить его на свою норму: вектор 
имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Формулировка
Пусть дано линейное пространство 
со скалярным произведением 
. Пусть 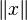— норма, порождённая скалярным произведением, то есть 
. Тогда для любых 
имеем:
причём равенство достигается тогда и только тогда, когда векторы и 
пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что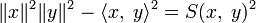 
, где 
— площадь параллелограмма, натянутого на векторы и .
В общем случае:
Примеры
· В пространстве комплекснозначных квадратично суммируемых последовательностей 
неравенство Коши — Буняковского имеет вид:
где 
обозначает комплексное сопряжение 
.
· В пространстве комплексных квадратично интегрируемых функций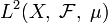 
неравенство Коши — Буняковского имеет вид:
· В пространстве случайных величин с конечным вторым моментом 
неравенство Коши — Буняковского имеет вид:
где 
обозначает ковариацию, а 
— дисперсию.
Доказательство
· Если 
то 
верно следующее
Значит дискриминант многочлена 
неположительный, то есть
Следовательно,
· Если 
то представим скалярное произведение в тригонометрическом виде 
Определим вектор 
Тогда
и
К скалярному произведению 
применим результат первого пункта доказательства.
Если длина вектора равна единице, он называется нормированным вектором: (x, x) = 1, |x| = 1.
Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.
Если векторы системы векторов e 1, e 2, ..., e n попарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (e i, e j) = 0, если i ≠ j, (e i, e i ) = 1.
Если e 1, e 2, ..., e n — ортонормированная система и x = x 1 e1 + x 2 e2 +... + x n e n — разложение вектора x по этой системе, то x i =(x, e i ).
№30
Квадратичные формы
Определение квадратичной формы
Квадратичная форма переменных 
- функция
- коэффициенты квадратичной формы. Без ограничения общности считают 
тогда
Если переменные принимают действительные значения и 
квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если 
Главные миноры матрицы A называются главными минорами квадратичной формы.
В пространстве 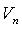квадратичную форму можно записать в виде 
где X - координатный столбец вектора 
В пространстве 
квадаратичную форму можно представить в виде 
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
