Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу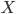 
из уравнения 
, необходимо умножить это уравнение на 
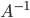слева.
Тогда: 
Следовательно, чтобы найти решение 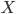уравнения , нужно найти обратную матрицу 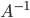и умножить ее на матрицу 
, стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если 
Решение: Так как обратная матрица равняется (см. пример 1)
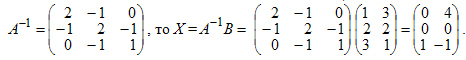
№22
Линейные пространства
Определение линейного пространства
Пусть V - непустое множество (его элементы будем называть векторами и обозначать 
...), в котором установлены правила:
1) любым двум элементам 
соответствует третий элемент 
называемый суммой элементов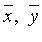 
(внутренняя операция);
2) каждому 
и каждому 
отвечает определенный элемент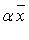 
(внешняя операция).
Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
I. 
II. 
III. 
(нулевой элемент, такой, что 
).
IV. 
(элемент, противоположный элементу 
), такой, что 
V. 
VI.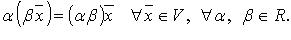 
VII. 
VIII. 
Аналогично определяется комплексное линейное пространство (вместо R рассматривается C).
Подпространство линейного пространства
Множество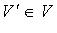 
называется подпространством линейного пространства V, если:
1) 
2) 
№23
Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из L линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов e 1,..., e n
образует базис в L если любой вектор x из L может быть представлен в виде
x = С1· e 1+С2 ·e 2+...+С n · e n.
Можно определить базис иначе.
Любая упорядоченная линейно независимая система e 1,..., e n векторов n- мерного линейного пространства Ln образует базис этого пространства.
Поскольку n, размерность пространства Ln — максимальное количество линейно независимых векторов пространства, то система векторов x, e 1,..., e n линейно зависима и, следовательно, вектор x линейно выражается через векторы e 1,..., e n:
x = x 1· e 1+ x 2 ·e 2+...+ xn · e n.
Такое разложение вектора по базису единственно.
Теорема 1. (О числе векторов в линейно независимых и порождающих системах векторов.) Число векторов в любой линейно независимой системе векторов не превосходит числа векторов в любой порождающей системе векторов этого же векторного пространства.
Доказательство. Пусть 
произвольная линейно независимая система векторов, 
- произвольная порождающая система. Допустим, что 
.
Мы можем считать, что все векторы порождающей системы ненулевые, т.к. нулевые векторы можно удалить из системы и оставшаяся система векторов, очевидно, остается порождающей.
Т.к. порождающая система, то она представляет любой вектор пространства, в том числе и вектор 
. Присоединим его к этой системе. Получаем линейно зависимую и порождающую систему векторов: 
. Тогда найдется вектор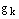 
этой системы, который линейно выражается через предыдущие векторы этой системы и его, в силу леммы, можно удалить из системы, причем оставшаяся система векторов будет по-прежнему порождающей.
Перенумеруем оставшуюся систему векторов: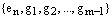 
. Т.к. эта система порождающая, то она представляет вектор 
и, присоединяя его к этой системе, опять получаем линейно зависимую и порождающую систему: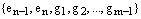 
.
Далее все повторяется. Найдется вектор в этой системе, который линейно выражается через предыдущие, причем это не может быть вектор , т.к. исходная система линейно независимая и вектор не выражается линейно через вектор . Значит, это может быть только один из векторов 
. Удаляя его из системы 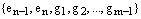, получаем, после перенумерования, систему 
, которая будет порождающей системой. Продолжая этот процесс, через 
шагов получим порождающую систему векторов: 
, где 
, т.к. по нашему предположению . Значит, эта система, как порождающая, представляет и вектор 
, что противоречит условию линейной независимости системы .
Теорема 1 доказана.
Теорема 2. (О количестве векторов в базисе.) В любом базисе векторного пространства содержится одно и тоже число векторов.
Доказательство. Пусть и – два произвольных базиса векторного пространства. Любой базис является линейно независимой и порождающей системой векторов.
Т.к. первая система линейно независимая, а вторая – порождающая, то, по теореме 1, 
.
Аналогично, вторая система линейно независимая, а первая – порождающая, то 
. Отсюда следует, что 
, ч.т.д.
Теорема 2 доказана.
Данная теорема позволяет ввести следующее определение.
Определение. Размерностью векторного пространства V над полем K называется число векторов в его базисе.
Обозначение: 
или 
.
№24
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где 
— координаты вектора.
Свойства
· Равные векторы в единой системе координат имеют равные координаты
· Координаты коллинеарных векторов пропорциональны:
Подразумевается, что координаты вектора 
не равны нулю.
· Квадрат длины вектора равен сумме квадратов его координат:
· При умножении вектора на действительное число каждая его координата умножается на это число:
· При сложении векторов соответствующие координаты векторов складываются:
· Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
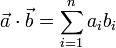
· Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
где
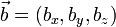
· Аналогично, смешанное произведение трех векторов можно найти через определитель
Ма́трицей перехо́да от базиса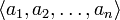 
к базису 
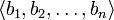является матрица, столбцы которой — координаты разложения векторов 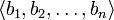в базисе .
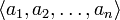Обозначается 
Представление
Так как
.
.
.
.
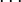Матрица перехода это
Свойства
· Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.
· 
№25
Линейные подпространства
Рассмотрим некоторое подмножество X1 линейного пространства X, т.е. X1 Н X.
Определение. Подмножество X1 линейного пространства X называется линейным подпространством, если для любых векторов x, y О X1 и любого числа α:
x + y О X1;
αx О X1.
Рассмотрим два линейных подпространства X1 и X2 линейного пространства X.
Если любой вектор x О X может быть единственным образом представлен в виде x = x1 + x2, где x1 О X1 и x2 О X2, то говорят, что пространство X разложено в прямую сумму подпространств X1 и X2.
Прямая сумма обозначается X = X1 + X2.
Любое линейное пространство может быть разложено в прямую сумму нескольких подпространств. В частности, разложение вектора по базису связано с разложением n–мерного пространства в прямую сумму n одномерных подпространств.
Я НЕ НАШЕЛ «ПОДПРОСТРАНСТВА ПРОСТРАНСТВА R3»
№26
Матрица линейного преобразования
В примере 19.4 было показано, что преобразование 
-мерного пространства, заключающееся в умножении координатных столбцов векторов на фиксированную матрицу, является линейным преобразованием. В этом разделе мы покажем, что все линейные преобразования конечномерного пространства устроены таким же образом.
Пусть 
-- -мерное линейное пространство, в котором задан базис 
, 
-- линейное преобразование. Возьмем произвольный вектор 
. Пусть 
-- его координатный столбец. Координатный столбец вектора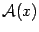 
обозначим 
.
Запишем разложение вектора по базису пространства 
. Для образа этого вектора получим
| (19.2) |
Векторы 
имеют какие-то координатные столбцы, обозначим их 
, 
,..., 
соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,
Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования
Это равенство означает, что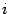 
-той координатой вектора 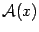служит 
.
Составим матрицу 
из координатных столбцов векторов 
,..., 
Вычислим произведение матрицы на столбец 
Мы видим, что 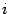-ый элемент столбца совпадает с 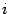-ой координатой вектора 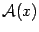. Поэтому
| (19.3) |
Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора.
Матрица называется матрицей линейного преобразования . Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д.
Пример 19.5 Найдем матрицу линейного преобразования из примера 19.1.
Выберем какой-нибудь базис 
. Тогда
Следовательно, первый столбец матрицы имеет вид 
. Аналогично
Второй столбец матрицы имеет вид 
. В итоге
Пример 19.6 Найдем матрицу линейного преобразования из примера 19.2. Угол 
возьмем равным 
. В качестве базиса возьмем привычный ортонормированный базис i, j.
Из рисунка 19.7 видно, что вектор 
имеет координаты 
и 
.
Рис.19.7.Координаты образов базисных векторов при преобразовании поворота
Поэтому координатный столбец образа первого базисного вектора имеет вид 
. Координаты образа второго базисного вектора равны 
и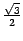 
, его координатный столбец имеет вид 
. В итоге получаем, что в базисе i, j матрица поворота на угол имеет вид
№26
Действия с линейными преобразованиями.
