Лекция 6. Понятие о логарифмической производной. Производные высших порядков. Теоремы Роля, Лагранжа, Коши. Правило Лопиталя. Исследование функций и построение графиков с применением производных.
Производная логарифмической функции
Рассмотрим логарифмическую функцию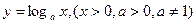 
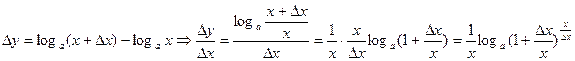. Переходя к пределу при 
получим 
. Следовательно 
. В частности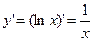 
Понятие о логарифмической производной
Рассмотрим сложную функцию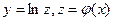 
Применяя правило дифференцирования сложной функции, получаем
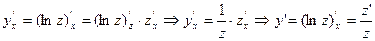
Производная от логарифмической функции называется логарифмической производной функции.
Пример 
Таблица формул дифференцирования
| №пп | Функция и ее производная |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
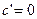
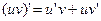
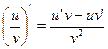
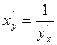
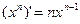
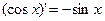
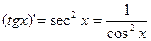
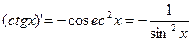
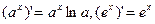
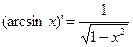
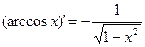
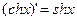
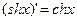
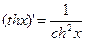
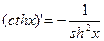
Производная функции, заданной параметрическими уравнениями
Зависимость между переменными x,y иногда удобно задавать двумя уравнениями 
(1), где t – вспомогательная переменная, (параметр). Например, в механике t – время, уравнения (1) – параметрические уравнения траектории движущейся точки.
В общем случае, уравнения (1) определяют y как сложную функцию относительно x. Разрешив первое уравнение системы (1) относительно параметра t (если это возможно), получим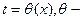 
функция, обратная к функции 
.
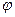Далее, исключая из уравнений (1) параметр t, получаем 
(2). Пользуясь формулой (2) легко найти производную 
как производную сложной функции.
Кроме того, существует правило для нахождения , не требующее исключение параметра t ( параметр невозможно исключить).
Теорема
Если функция y аргумента x задана параметрическими уравнениями , где 
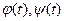- дифференцируемые функции и 
, то производная этой функции есть 
(3)
Доказательство
В цепочке равенств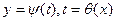 
, где 
- обратная функция по отношению к функции 
, будем рассматривать t как промежуточный аргумент. Тогда, согласно правила дифференцирования сложной функции будем иметь
(4)
Применяя правило дифференцирования обратной функции получим 
(5). Из (4) и (5) получаем .
В обозначениях Лейбница 
Пример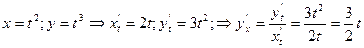 
Производные высших порядков
Производная f’(x) функции f(x) называется производной первого порядка и представляет собой некоторую новую функцию. Вполне допустимо, что эта функция сама имеет производную. Тогда производная от производной первого порядка называется производной второго порядка или второй производной.
Обозначение
f”(x)=[f’(x)]’
Производная от производной второго порядка, если она существует называется производной третьего порядка или третьей производной
Обозначение
f”’(x)=[f”(x)]’ и так далее.
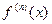- производная n – го порядка.
Пример
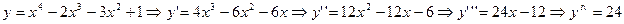
Производные высших порядков от функции, заданной параметрическими уравнениями
Пусть функция y аргумента x задана параметрическими уравнениями , (1) где 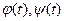- дифференцируемые функции и , 
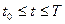. Причем на отрезке 
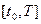функция имеет обратную функцию .
Для первой производной имеет место формула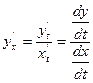 
(2).
Для нахождения второй производной 
дифференцируем по х равенство (2) имя в виду, что t есть функция от х.
или 
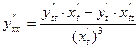(3)
Аналогичным образом можно найти производные 
Пример
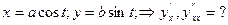
Решение
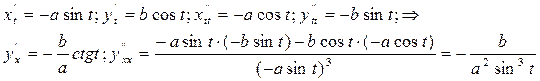
Формула Лейбница
На производные высших порядков распространяются общие правила дифференцирования. Если u=u(x), v=v(x) – дифференцируемые функции, то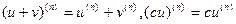 
.
Выведем формулу Лейбница, дающую возможность вычислить производную n – го порядка от произведения двух функций, то есть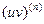 
. Для того, чтобы вывести эту формулу найдем сначала несколько производных, а затем установим общий закон, пригодный для вычисления производной любого порядка.
y=uv
…
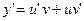
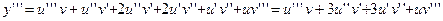
Закон составления производных сохраняется для производных любого порядка и заключается в следующем:
Надо выражение 
разложить по формуле бинома Ньютона и в полученном выражении, заменить показатели степеней для u и v указателями порядка производных, причем нулевые степени (
, входящие в крайние элементы разложения, надо заменить самими функциями (то есть производными нулевого порядка).
Получаем
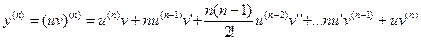- формула Лейбница.
Строгое доказательство этой формулы можно было бы провести методом математической индукции.
Пример
Решение
…
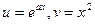
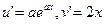
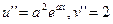
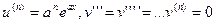, тогда
