Теорема 1
Сумма двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Доказательство
Пусть 
- бесконечно малые последовательности.
Докажем, что 
- бесконечно малая последовательность
Пусть 
- произвольное число.
- номер, начиная с которого 
- номер, начиная с которого 
Так как 
, то, обозначая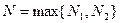 
, получаем, что, начиная с некоторого номера N выполняется неравенство 
. Это означает, что последовательность - бесконечно малая.
Теорема 2
Разность двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Доказательство аналогичное, только, вместо берем 
Следствие Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3
Бесконечно малая последовательность ограничена.
Доказательство
Пусть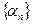 
- бесконечно малая последовательность. Пусть - произвольное число. Пусть N – номер, начиная с которого 
. Обозначим через 
. Очевидно, что 
для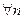 
, что означает ограниченность последовательности.
Теорема 4
Произведение ограниченной последовательности на бесконечно малую последовательность представляет собой бесконечно малую последовательность.
Доказательство
Пусть 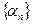- бесконечно малая последовательность;
Пусть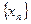 
- ограниченная последовательность.
Так как 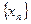- ограниченная последовательность, то 
, что 
. Возьмем - произвольное число. Так как 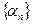- бесконечно малая последовательность, то для положительного числа 
можно указать N такой, что при 
выполняется неравенство 
. Тогда при 
. Поэтому последовательность 
- бесконечно малая.
Следствие
Произведение любого конечного числа бесконечно малых последовательностей представляет собой бесконечно малую последовательность.
Замечание
Частное двух бесконечно малых последовательностей может быть последовательностью любого типа и даже может не иметь смысла.
Например
бесконечно большая последовательность
бесконечно малая последовательность
Если бесконечно много элементов последовательности 
равны 0, то последовательность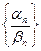 
не имеет смысла.
Теорема 5
Если все элементы бесконечно малой последовательности равны одному и тому же числу с, то с=0.
Доказательство
Пусть 
, положим 
. Начиная с номера N, соответствующему этому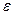 
выполняется неравенство . Так как 
, а , то 
- противоречие.
Теорема 6
Если 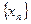- бесконечно большая последовательность, то, начиная с некоторого номера n определена последовательность 
, которая является бесконечно малой последовательностью. Если все элементы бесконечно малой последовательности 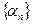не равны 0, то последовательность 
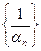- бесконечно большая.
Доказательство
Отметим, что у бесконечно большой последовательности лишь конечное число элементов может быть равно 0. Из определения бесконечно большой последовательности вытекает, что для данного A>0, существует N, начиная с которого 
. Это означает, что при все элементы 
, тогда последовательность имеет смысл, если ее элементы рассматривать, начиная с номера 
. Докажем теперь, что бесконечно малая последовательность. Пусть - произвольное число. Для числа 
, такой, что при выполняется неравенство 
. Поэтому, начиная с указанного номера N. Будет выполняться неравенство 
, то есть доказано, что последовательность - бесконечно малая.
Доказательство второй части теоремы проводится аналогично.
