Связь операций сложения и умножения

Лекция 1. Последовательности. Основные понятия и определения.

Действительные числа

Множество всех действительных чисел обозначается R. Его подмножества называются числовыми.

1. Операции сложения. Для любой пары действительных чисел a и b определено единственное число, называемое их суммой и обозначаемое a+b, такое, что при этом выполняются следующие условия:

1.1

1.2

1.3 Существует такое число, называемое нулем и обозначаемое 0, что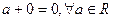

1.4 Для любого числа , существует число называемое ему противоположным и обозначаемое – а, для которого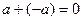

Число называется разностью чисел и обозначается

 

2. Операции умножения. Для любой пары действительных чисел a и b определено

единственное число, называемое их произведением и обозначаемое ab, такое, что при

этом выполняются следующие условия:

2.1

2.2

2.3Существует такое число, называемое единицей и обозначаемое 1, что

2.4 Для любого числа существует число называемое ему обратным и обозначаемое 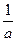, для которого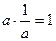

Связь операций сложения и умножения

1. Упорядоченность

Для любых двух различных чисел a и b имеет место одно из двух соотношений: либо

4.1 транзитивность. Если a<b и b<c, то a<c

4.2 если a<b, то для любого числа c имеет место a+c<b+c

4.3 если a>b и c>0, то ac>bc

 

1. Непрерывность. Для любых непустых числовых множеств Х и У, таких что для каждой пары чисел выполняется неравенство , существует число а, удовлетворяющее условию

Х У

_________|_|_|_|_|_______________|_|_|_|_|___________

 

х а у

Определение. Множество элементов, обладающих свойствами 1-5, содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент – действительным числом.

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел.

Для любого числа и натурального n степень определяется как произведение n сомножителей, равных a.

Пусть a>0, а n натуральное число. Число b называется корнем n -й степени из числа a, если . Обозначение 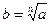. Неотрицательное значение корня называется его арифметическим значением.

Если , где p и q – целые, , т. е. r –рациональное число, то для a>0

Для любого числа неотрицательное число называется абсолютной величиной или модулем. Свойства модуля

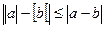
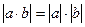
Расширенная числовая прямая. Окрестности.

Геометрически множество действительных чисел изображается направленной прямой, а отдельные числа - точками этой прямой. Поэтому совокупность действительных чисел часто называют числовой прямой или числовой осью, а отдельные числа – ее точками.

Часто бывает удобно дополнить множество действительных чисел элементами, обозначаемыми через 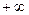и - (плюс бесконечность и минус бесконечность). Считаем по определению, что выполняется неравенство . Множество действительных чисел R дополненное этими символами называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается . Бесконечности называются также бесконечно удаленными точками числовой прямой, остальные точки называются конечными точками числовой прямой.

Напомним определения некоторых важных типов подмножеств расширенной числовой прямой .

Пусть

Множество 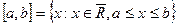- отрезок;

Множество - интервал;

Множество - полуинтервал;

Множество - полуинтервал;

Все они – промежутки расширенной числовой прямой.

a,b – концы промежутков;

a<x<b – x – внутренние точки;

b-a – длина промежутка (сам промежуток – конечный).

Важным является понятие окрестности конечной и бесконечно удаленной точки числовой прямой.

Если , то - окрестностью числа а называется интервал , то есть

В случае

В случае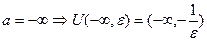

Предел последовательности

Одной из важнейших операций мат. Анализа является операция предельного перехода. Рассмотрим простейшую форму предельного перехода, основанную на понятии предела числовой последовательности.

1. Числовые последовательности

В элементарном курсе математики было дано понятие последовательности, и примерами могут служить арифметическая и геометрическая прогрессия.

Определение Если каждому числу n натурального ряда чисел 1,2,3,…,n,… ставится в соответствие по определенному закону некоторое вещественное число , то множество занумерованных чисел

(1)

называются числовой последовательностью. Обозначение последовательности 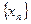. Элемент или член последовательности . Например, соответственно

Введем понятие арифметических операций над числовыми последовательностями. Пусть даны последовательности . Соответственно:

или - сумма последовательностей;

или - разность последовательностей;

или 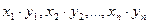- произведение последовательностей;

или - частное последовательностей.

1. Ограниченные и неограниченные последовательности

Определение 1. Последовательность 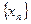называется ограниченной сверху (снизу), если существует такое число M (число m), что каждый элемент последовательности 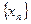удовлетворяет неравенству

M – верхняя грань; m – нижняя грань. - условие ограниченности последовательности сверху (снизу).

Замечание Любая ограниченная сверху (снизу) последовательность имеет бесчисленное множество верхних (нижних) граней.

 

Определение 2. Последовательность 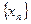называется ограниченной с обеих сторон или просто ограниченной, если существует такие числа M и m, что каждый элемент последовательности 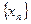удовлетворяет неравенству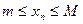

M – верхняя грань; m – нижняя грань.

Если 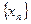ограничена, то все элементы этой последовательности удовлетворяют неравенству , где

Определение 3. Последовательность 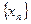называется неограниченной, если для любого положительного числа А найдется элемент этой последовательности, удовлетворяющий неравенству .

Примеры:

1) последовательность -1, -4, -9, …,- ,… - ограничена сверху и не ограничена снизу. Верхняя грань – число больше или равно -1.

2) Последовательность 1, ½,1/3,…,1/n, … - ограничена.

3) Последовательность 1, 2, 1, 3, ….,n, 1, (n+1), … - не ограничена.

1. Бесконечно большие и бесконечно малые последовательности.

Введем определения бесконечно больших и бесконечно малых последовательностей.

Определение 1. Последовательность 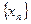называется бесконечно большой, если для любого положительного числа А можно указать номер N такой, что для все элементы удовлетворяют неравенству

Замечание 1

Любая бесконечно большая последовательность является неограниченной.

Замечание 2

Неограниченная последовательность может и не быть бесконечно большой.

Пример

Неограниченная последовательность 1,2,1,3,…,n,… не является бесконечно большой, поскольку при А>1 неравенство 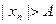не имеет места для всех элементов с нечетными номерами.

Определение 2

Последовательность 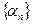называется бесконечно малой, если для , можно указать номер N такой, что при все элементы этой последовательности удовлетворяют неравенству .

Рассмотрим пример

Последовательность

При |q|>1 – бесконечно большая;

При |q|<1 – бесконечно малая.

Докажем первое утверждение

Если |q|>1, то . Используя формулу бинома Ньютона, получаем

элементы. Отсюда .

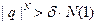Фиксируем и выбираем номер N столь большим, чтобы имело место неравенство . Из этого неравенства и неравенства (1) следует неравенство . Так как, при . Тем самым доказано, что при |q|>1 рассматриваемая последовательность является бесконечно большой.

Второе утверждение доказывается аналогично, применяя бином Ньютона и определение бесконечно малой последовательности.