Разложим в ряд Маклорена функцию sinx. Для этого последовательно находим значения ее производных в точке х=0
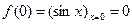
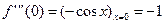
и т.д.
Значения производных повторяются и образуют периодическую последовательность
0,1,0,-1,0,1,0,-1,...
Любая производная функции sinx (то есть 
следовательно ряд функции sinx сходится к ней на всей числовой оси.
Итак
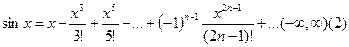
Аналогично для функции cosx
- Биноминальный ряд
Рассмотрим функцию 
, где m – любое число. Разложим функцию в ряд Маклорена.
…
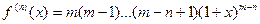
поэтому 
. Следовательно, ряд запишется в виде:
Установим область сходимости ряда. Найдем предел абсолютной величины отношения последующего элемента к предыдущему
согласно признака Даламбера ряд сходится, если |x|<1 и расходится, если |x}>1.
Исследуем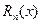 
, ограничившись случаем, когда 0<x<1. В этом интервале для всех n>m-1 имеем 
и поэтому 
Воспользуемся неравенством (***) 
. Правая часть неравенства есть абсолютная величина (n+1)-го члена степенного ряда, сходящегося при |x|<1. Следовательно, 
. Соответствующее доказательство для интервала
(-1,0) более сложное и оно не приводится.
Таким образом, биноминальный ряд представляет функцию в интервале (-1,1)
Если m – целое положительное число, то ряд справа содержит всего (m+1) слагаемых и превращается в форму бинома Ньютона. Заметим, что ряд сходится к функции во всем замкнутом интервале [-1,1].
Приведем биноминальные ряды, соответствующие значениям m=-1, m=1/2, m=-1/2.
(это геометрическая прогрессия)
Замечание
Разложение отдельных функций в ряды могут быть получены из уже известных разложений с помощью свойств степенных рядов.
4. Функции ln(1+x) и arctgx
Для разложения в ряд Маклорена функции f(x)=ln(1+x) воспользуемся формулой для суммы геометрической прогрессии
Применим теорему об интегрировании степенных рядов и проинтегрируем ряд в пределах от 0 до х. Поскольку 
, то интегрируя поэлементно ряд, получим 
.
Совершенно аналогично получается разложение функции arctg x в ряд Маклорена. Для этого, заменим в формуле для суммы элементов геометрической прогрессии x на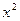 
. Получим 
. Проинтегрируем ряд в пределах от 0 до х. Считая, что |x|<1 получаем 
Замечание
Разложения (1)-(6) могут быть использованы для разложения в ряды других функций. Примеры:
1) Разложим в ряд Маклорена гиперболические функции chx и shx
Для ряда (1) заменим 
на 
получим 
. Далее, по правилу сложения и вычитания рядов находим искомое разложение
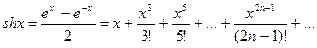
2) Разложим в ряд Маклорена функцию 
Возьмем разложение функции и вместо , подставим получим
3) Разложим в ряд Маклорена функцию 
Воспользуемся разложением биноминального ряда, где m=-1/2 и, для 
заменим x на 
, получим
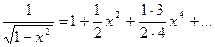(*). Умножим обе части на 
4) Разложим в ряд Маклорена функцию 
Так как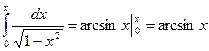 
. То разложение arcsinx получается интегрированием ряда (*)
5) Разложим в ряд Маклорена функцию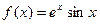 
Так как ряды для и sinx сходятся абсолютно, то, перемножая их по правилу, рассмотренному ранее получим искомое разложение
(первые коэффициенты, так как закон подметить трудно).
