Перейдем теперь к выяснению условий, при которых можно утверждать, что ряд Тейлора, составленный для функции f(x)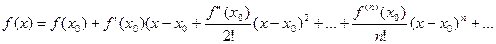 
действительно сходится в некотором интервале и что его сумма в точности равна f(x).
Обозначения:
- многочлен n-ой степени, представляющий n -ую частичную сумму ряда Тейлора 
Сходимость ряда Тейлора к функции f(x) в точке х означает, что 
или, что то же самое, 
.
Величина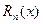 
дает при этом как раз ту ошибку, которую мы делаем, заменяя функцию f(x) многочленом .
Для оценки величины остаточного члена, служит теорема, которую докажем позднее.
Частный случай
Предположим, что функция f(x) сама есть многочлен n -ой степени. Тогда при последовательном дифференцировании функции f(x) будем каждый раз получать многочлен степени на единицу меньше. После n -го дифференцирования получаем постоянную величину и все последующие производные равны 0. Таким образом, от ряда Тейлора для многочлена f(x) останутся только первые n+1 слагаемых, то есть опять-таки многочлен n -ой степени. Полученное тождество
называется формулой Тейлора для многочлена.
Пример
Разложить многочлен 
по степеням x-1.
Решение:
Здесь 
Таким образом 
Остаточный член ряда Тейлора. Формула Тейлора.
Пусть f(x) – функция, относительно которой хотим выяснить, допускает она разложение в ряд Тейлора в окрестности некоторой точки 
или нет.
Запишем ее в следующем виде
, где
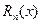- остаточный член ряда Тейлора.
Рассмотрим теорему относительно структуры 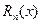, которая в дальнейшем позволит устанавливать, стремится ли 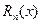к нулю при неограниченном возрастании n или нет, то есть можно ли представить функцию в виде ряда Тейлора или нет.
Теорема
Если функция f(x) во всех точках некоторого интервала, содержащего точку , имеет (n+1) производную 
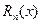, то остаточный член для любой точки этого интервала имеет вид 
, где 
заключено между x и 
В соответствии с такой записью 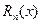формула (*) имеет вид
В таком виде эту формулу называют формулой Тейлора n -го порядка для функции f(x) в точке . Последний член в этой формуле отличается от общего члена суммы только тем, что значение соответствующей производной берется не в точке , а в некоторой точке , лежащей между точками и х.
Некоторые частные случаи этой формулы:
1) Пусть n=0, тогда 
. Это формула Лагранжа.
2) Пусть n=1, тогда 
. Если в этой формуле отбросить остаточный член, то получим приближенное значение функции, основанное на применении дифференциала. 
. При этом f(x) заменяется линейной функцией.
Само по себе выражение для остаточного члена 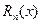не дает возможности вычислять его величину, так как неизвестна точка , в которой берется (n+1) производная.
Поэтому в дальнейшем ограничимся оценкой величины 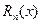. Это делается на основании следующего замечания:
Пусть в интервале, в котором справедлива формула Тейлора, по абсолютной величине не превосходит числа 
:
, тогда для любого х из этого интервала остаточный член 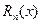удовлетворяет неравенству 
(***)
Действительно, согласно доказанной теоремы 
