Если ряд сходится, то общий элемент стремится к нулю при возрастании его номера.
Доказательство
Имеем 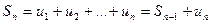 . Если ряд сходится, то
. Если ряд сходится, то 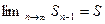 и
и 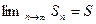 . Поскольку
. Поскольку 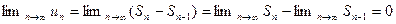
Из доказанного вытекает достаточный признак расходимости ряда.
Если 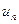 не стремится к нулю, то ряд не может быть сходящимся.
не стремится к нулю, то ряд не может быть сходящимся.
Пример
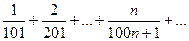 ряд расходится, так как
ряд расходится, так как 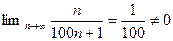
Следует помнить, что стремление n -го элемента к нулю не является достаточным для сходимости ряда.
Рассмотрим ряд 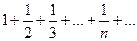 - гармонический ряд.
- гармонический ряд.
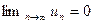 , но ряд расходится. Покажем, что
, но ряд расходится. Покажем, что 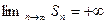 . Для доказательства заменим некоторые элементы ряда меньшими числами и убедимся, что даже сумма меньших слагаемых будет стремиться к бесконечности.
. Для доказательства заменим некоторые элементы ряда меньшими числами и убедимся, что даже сумма меньших слагаемых будет стремиться к бесконечности.
Сделаем разбиение ряда на группы
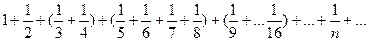
Следующая замена
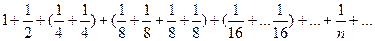 сумма каждой скобки равна
сумма каждой скобки равна 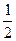 . Поскольку таких скобок можно брать сколько угодно, то сумма стремится к бесконечности.
. Поскольку таких скобок можно брать сколько угодно, то сумма стремится к бесконечности.
Таким образом, частичные суммы ряда неограниченно возрастают, следовательно, ряд расходится.
Пример
 ряд расходится, так как даже при выполнении необходимого признака
ряд расходится, так как даже при выполнении необходимого признака 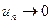 при
при 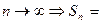
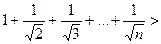
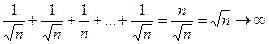
Ряды с положительными элементами. Достаточные признаки сходимости.
- Признаки сравнения
Рассмотрим ряд 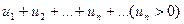
Лемма Если частичные суммы ряда с положительными элементами ограничены сверху, то ряд сходится. (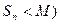
Доказательство
Так как 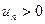 , то частичные суммы ряда по мере возрастания числа элементов тоже возрастают
, то частичные суммы ряда по мере возрастания числа элементов тоже возрастают 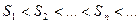
Но если последовательность монотонно возрастает и ограничена сверху, то по признаку Вейерштрасса она имеет предел, также не превосходящий числа М. Следовательно, имеем 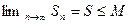 . Верно обратное. Если ряд с положительными элементами сходится, то его частичные суммы меньше суммы ряда:
. Верно обратное. Если ряд с положительными элементами сходится, то его частичные суммы меньше суммы ряда: 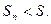
Замечание
Если ряд с положительными элементами расходится, то его частичные суммы стремятся к бесконечности, то есть 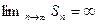 или другая запись
или другая запись 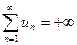 .
.
Признак сравнения
Пусть даны два ряда с положительными элементами:
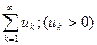 (1) и
(1) и 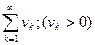 (2) и пусть каждый элемент ряда (1) не больше соответствующего элемента ряда (2)
(2) и пусть каждый элемент ряда (1) не больше соответствующего элемента ряда (2) 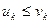 (*). Тогда
(*). Тогда
1) Если сходится ряд (2), то сходится и ряд (1)
2) Если расходится ряд (1), то расходится и ряд (2)
Доказательство
Докажем первую часть теоремы. Полагаем 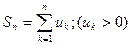 ,
, 
По условию ряд (2) сходится, поэтому 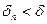 , где
, где 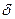 - сумма ряда (2). А из условия (*) следует, что
- сумма ряда (2). А из условия (*) следует, что 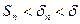 . Получаем, что частичные суммы ряда (1) ограничены сверху. В силу доказанной выше леммы ряд (1) сходится.
. Получаем, что частичные суммы ряда (1) ограничены сверху. В силу доказанной выше леммы ряд (1) сходится.
Для доказательства второй части достаточно заметить, что, поскольку ряд (1) расходится, то его суммы неограниченно возрастают:  .
.
Так как  , то и
, то и 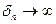 . Следовательно ряд (2) расходится.
. Следовательно ряд (2) расходится.
Признаки сравнения применимы и в том случае, когда условию (*) удовлетворяют элементы ряда не при всех n, а лишь начиная с некоторого n=N. Это следует из третьего свойства сходящихся рядов.
Примеры:
1. Ряд  расходится, так как гармонический ряд
расходится, так как гармонический ряд 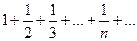 расходится, а
расходится, а 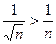 при n>1
при n>1
2. Ряд  сходится, так как сходится ряд
сходится, так как сходится ряд 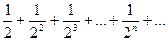 (убывающая геометрическая прогрессия) и
(убывающая геометрическая прогрессия) и 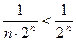
Замечание
На практике признаки сравнения наиболее удобно применять в следующем виде:
Если 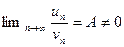 , то ряды (1) и (2) или оба сходятся, или оба расходятся.
, то ряды (1) и (2) или оба сходятся, или оба расходятся.
Доказательство
Из определения предела следует, что для всякого  можно указать такое число N, что при всех n>N будет справедливо неравенство
можно указать такое число N, что при всех n>N будет справедливо неравенство 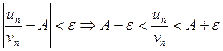 , где
, где  настолько мало, что
настолько мало, что 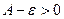 .
.
Предположим сначала, что ряд (2) сходится. Тогда по свойству (1) сходится и ряд с общим элементом 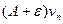 и по признаку сравнения сходится ряд (1), так как
и по признаку сравнения сходится ряд (1), так как 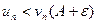 .
.
Наоборот, если ряд (2) расходится, то из неравенства 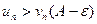 будет следовать, что расходится ряд (1).
будет следовать, что расходится ряд (1).
Пример: Ряд 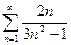 расходится, так как, выбирая
расходится, так как, выбирая 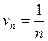 - гармонический ряд и вычисляем
- гармонический ряд и вычисляем 
В качестве эталонов для сравнения рядов выбирают: гармонический ряд – расходящийся; бесконечно убывающая геометрическая прогрессия или ряд обратных квадратов – сходящиеся.
Признак Даламбера
Рассмотрим ряд 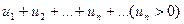 (*)
(*)
Если при  существует предел отношения последующего элемента к предыдущему, то есть
существует предел отношения последующего элемента к предыдущему, то есть 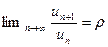 , то при
, то при
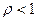 - ряд сходится;
- ряд сходится; 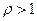 - ряд расходится;
- ряд расходится; 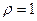 - признак Даламбера не действует.
- признак Даламбера не действует.
Доказательство
Пусть 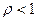 . В силу определения предела всегда можно выбрать такое число N. Что при всех
. В силу определения предела всегда можно выбрать такое число N. Что при всех  будет справедливо неравенство
будет справедливо неравенство
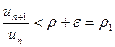 , где
, где  берется настолько малым, что
берется настолько малым, что 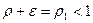
Тогда 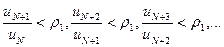 получаем неравенства
получаем неравенства
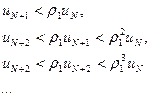
Отсюда вытекает, что элементы ряда  представляющего N -ый остаток данного ряда, меньше соответствующих элементов бесконечно убывающей геометрической прогрессии
представляющего N -ый остаток данного ряда, меньше соответствующих элементов бесконечно убывающей геометрической прогрессии
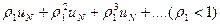
Следовательно N-ый остаток ряда сходится, тогда сходится и сам ряд.
Пусть 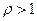 . В силу определения предела всегда можно выбрать такое число N. Что при всех
. В силу определения предела всегда можно выбрать такое число N. Что при всех  будет справедливо неравенство
будет справедливо неравенство

Но тогда каждый последующий элемент ряда будет больше предшествующего и, поскольку все они положительны, не может выполняться необходимый признак сходимости ряда, согласно которому общий элемент должен стремиться к нулю, то есть ряд расходится.
Примеры
1. Ряд 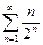 сходится, так как
сходится, так как 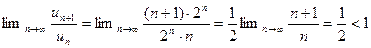
2. Рассмотрим ряд 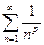
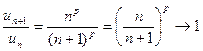 при
при  независимо от величины показателя p.
независимо от величины показателя p.
При p=1 – гармонический ряд (расходится);
При p=2 – ряд обратных квадратов (сходится).
Следовательно, при 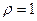 - признак Даламбера не действует.
- признак Даламбера не действует.
Радикальный признак Коши.
Рассмотрим без доказательства еще один достаточный признак сходимости знакоположительного ряда.
Рассмотрим ряд 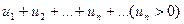 (*)
(*)
Если при  существует
существует 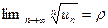 , то при
, то при
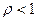 - ряд сходится;
- ряд сходится; 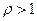 - ряд расходится;
- ряд расходится; 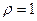 - радикальный признак Коши не действует.
- радикальный признак Коши не действует.
Пример. Ряд 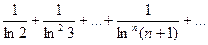 сходится, так как
сходится, так как 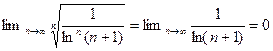
Интегральный признак Коши
Не трудно заметить полную аналогию определений сходимости ряда и сходимости несобственного интеграла с бесконечным верхним пределом. Много общего и в признаках сходимости рядов с положительными элементами и интегралов с положительной подынтегральной функцией.
Рассмотрим признак, позволяющий в некоторых случаях сводить вопрос о сходимости ряда, к вопросу о сходимости интеграла.
Рассмотрим ряд 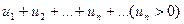 (*), элементы которого являются значениями непрерывной положительной функции f(x) при целых значениях аргумента х:
(*), элементы которого являются значениями непрерывной положительной функции f(x) при целых значениях аргумента х:
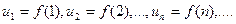 и пусть f(x) монотонно убывает в интервале
и пусть f(x) монотонно убывает в интервале 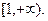 Тогда ряд сходится, если сходится несобственный интеграл
Тогда ряд сходится, если сходится несобственный интеграл 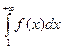 и расходится, если этот интеграл расходится.
и расходится, если этот интеграл расходится.
Доказательство
|

Рассмотрим криволинейную трапецию, ограниченную линией y=f(x), с основанием от x=1 до x=n, где n – произвольное положительное число. (см. Рис.). Площадь измеряется интегралом
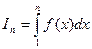
Отметим точки основания x=1, x=2, ….,x=n. Рассмотрим две ступенчатые фигуры. Одна из них (входящая) имеет площадь равную 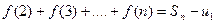 , а вторая (выходящая) – площадь равную
, а вторая (выходящая) – площадь равную 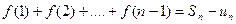 , где
, где 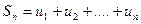 . Для представленных площадей справедливо
. Для представленных площадей справедливо 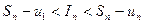 . Отсюда получаем два неравенства:
. Отсюда получаем два неравенства:
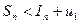 (1)
(1)
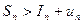 (2)
(2)
Так как f(x)>0, то  возрастает вместе с n. Возможны два случая:
возрастает вместе с n. Возможны два случая:
1) Несобственный интеграл сходится, то есть  существует, тогда
существует, тогда  и из неравенства (1) при всяком n находим
и из неравенства (1) при всяком n находим  , то есть
, то есть  - ограничена, тогда на основании леммы ряд сходится.
- ограничена, тогда на основании леммы ряд сходится.
2) Интеграл расходится: тогда  при
при  и на основании неравенства (2) следует, что
и на основании неравенства (2) следует, что  , то есть ряд расходится.
, то есть ряд расходится.
Пример
Рассмотрим ряд 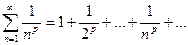 . Для этого ряда признак Даламбера не применим, так как
. Для этого ряда признак Даламбера не применим, так как 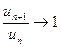 .
.
Применим интегральный признак. Подынтегральная функция  . Соответственно интеграл
. Соответственно интеграл 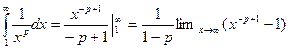
Если p>1, то 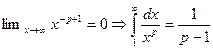 - интеграл сходится.
- интеграл сходится.
Если p<1, то интеграл расходится, так как 
При p=1 интеграл также расходится: 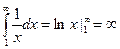
В итоге получаем:
При p>1 – ряд сходится
При p<1 – ряд расходится
Геометрическую идею, лежащую в основе доказательства интегрального признака Коши, можно применить для оценки ошибки, возникающей при приближенном вычислении суммы ряда, сходимость которого была установлена с помощью этого признака. Для этого нужно уметь оценивать величину разности
 , то есть остаток ряда
, то есть остаток ряда 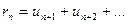 .
.  при любом n.
при любом n.
Приведенный рисунок показывает, что остаток ряда есть сумма “уходящих вправо” прямоугольников и она меньше, чем площадь заключающей их фигуры, поэтому
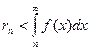
Применим эту формулу для лценки остатка только, что рассмотренного ряда 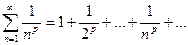 при p>1
при p>1

Если необходимо, чтобы величина остатка ряда не превышала заранее выбранного числа 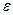 , то за номер n можно взять наименьшее целое число, удовлетворяющее неравенству
, то за номер n можно взять наименьшее целое число, удовлетворяющее неравенству
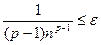
Пусть 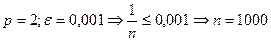 - это медленно сходящийся ряд.
- это медленно сходящийся ряд.
Пусть  - это ряд обратных кубов.
- это ряд обратных кубов.
Пусть 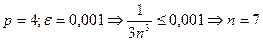 - быстро сходящийся ряд.
- быстро сходящийся ряд.






