Задача
Зная закон изменения площади поперечного сечения тела, найти объем этого тела
|
|
|
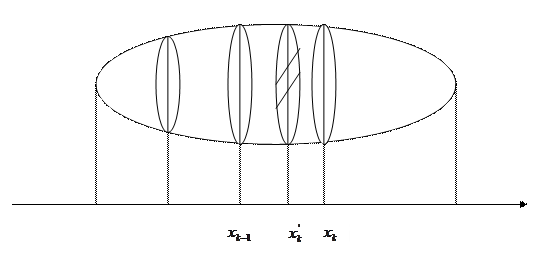
Пусть ОХ некоторое выбранное направление и S(x) – площадь поперечного сечения плоскостью перпендикулярной оси ОХ в точке с абсциссой х. Функцию S(x) будем предполагать известной и непрерывно меняющейся при изменении х. Проектируя тело на ось ОХ, получим некоторый отрезок [a,b], дающий линейные размеры тела в направлении оси ОХ.
Разобьем данное тело на элементарные слои плоскостями, перпендикулярными оси ОХ. Точки пересечения этих плоскостей с осью ОХ соответственно 
. Каждый элементарный слой, ограниченный плоскостями, пересекающимися в точках 
заменяем цилиндром с высотой 
и площадью основания 
. Объем данного цилиндра выражается формулой 
. Составим сумму всех таких произведений 
. Эта сумма является интегральной для данной функции S=S(x) на отрезке [a,b]. Она выражает объем ступенчатого тела, состоящего их элементарных цилиндров и приближенно заменяющего данное тело.
Объемом тела называют предел объема указанного ступенчатого тела, приближенно заменяющего данное тело, при 
- длина наибольшего из элементарных отрезков 
.
По определению 
с другой стороны 
. Из двух последних равенств получаем формулу вычисления объема тела по заданным поперечным сечениям.
(1)
Пример
Найти объем пирамиды с основанием В и высотой Н
Решение
Ось ОХ перпендикулярна поверхности В и направлена из точки О. S – площадь сечения пирамиды плоскостью, находящейся на расстоянии х от вершины. Так как площади поперечных сечений пирамиды относятся как квадраты расстояний их от вершины, то имеем
(известная формула)
Объем тела вращения
Задача
Найти объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции aABb, ограниченной данной непрерывной линией 
, отрезком 
оси ОХ и двумя вертикалями x=a, x=b
|
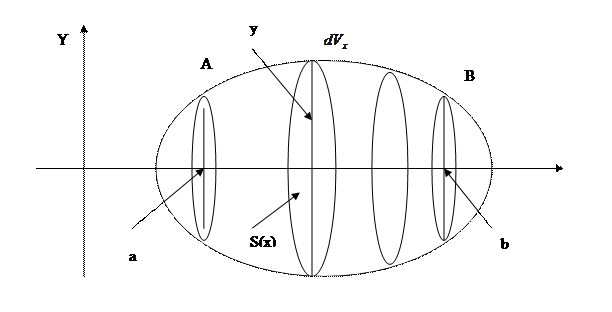
Эта задача – частный случай задачи, рассмотренной выше. Здесь площадь переменного поперечного сечения S=S(x), соответствующего абсциссе х, есть круг радиуса у, поэтому 
и формула (1) примет вид 
(2)
Задача
Найти объем тела, образованного вращением вокруг оси ОУ криволинейной трапеции cCDd, ограниченной данной непрерывной линией 
, отрезком 
оси ОУ и двумя горизонталями y=c, y=d
По аналогии с формулой (2) 
(3)
Примеры
- Вычислить объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями
Решение
Пределы интегрирования a=1,b=6, функция 
- Вычислить объем тела, полученного в результате вращения вокруг оси ОХ криволинейной трапеции, ограниченной линией
, осями координат и прямой х=1
Решение
Пределы интегрирования a=0,b=1, функция 
- Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса
вокруг оси ОХ (и ОУ)
Так ка эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси ОХ площади ОАВ, равной ¼ площади эллипса, и полученный результат удвоить.
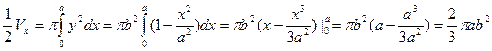. Окончательно 
и соответственно 
Несобственные интегралы
При определении интеграла 
(1) предполагалось, что:
1) Отрезок интегрирования [a,b] – конечен;
2) f(x) определена и непрерывна на отрезке [a,b].
Такой определенный интеграл называется собственным (название опускается).
Если нарушается по крайней мере одно из двух условий 1) или 2), то (1) называется несобственным определенным интегралом.
Рассмотрим смысл этого понятия для двух простейших случаев
I. Пусть f(x) непрерывна при 
. Тогда по определению полагают
(2)
Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), называется сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.
Геометрическая интерпретация
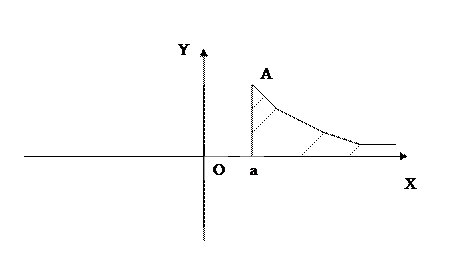
Геометрически для неотрицательной на 
функции f(x) несобственный интеграл (2) представляет собой площадь криволинейной фигуры, ограниченной данной линией y=f(x), осью ОХ и вертикалью х=а.
Пусть F(x) первообразная для f(x). На основании формулы (2) имеем
. Если ввести условное обозначение
, то получим для сходящегося несобственного интеграла с бесконечным верхним пределом обобщенную формулы Ньютона-Лейбница
(3), где F’(x)=f(x).
Примеры
1) 
2) Установить, при каких значениях 
интеграл 
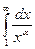сходится и при каких расходится
Решение Так как при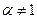 
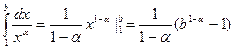, то
. Следовательно, можно сделать следующие выводы:
Если 
, то 
- интеграл сходится;
Если 
, то 
- интеграл расходится;
Если 
, то 
- интеграл расходится;
3. Вычислить 
(второй интеграл равен 
(см. Пример 1)).
Вычислим 
следовательно 
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, оценить его значение. Для этого могут быть полезны следующие теоремы.
Теорема 1
Если для любого х 
выполняется неравенство 
и если 
сходится, то 
также сходится, при этом 
- Исследовать, сходится ли интеграл
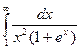
Решение
При 
сходится и его значение меньше или равно 1.
Теорема 2
Если для любого х выполняется неравенство 
и если расходится, то также расходится.
- Исследовать, сходится ли интеграл
Решение
При 
следовательно расходится и данный интеграл.
Для функции меняющий знак в бесконечном интервале, имеет место следующая теорема
Теорема 3
Если интеграл 
сходится, то сходится и интеграл . В этом случае последний интеграл называется абсолютно сходящимся.
- Исследовать, сходится ли интеграл
Решение
При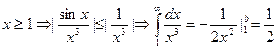 
следовательно сходится и данный интеграл.
