Логарифмическая производная
При дифференцировании показательно-степенной функции  обычно используют логарифмическую производную
обычно используют логарифмическую производную 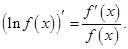 Делается это так:
Делается это так:

Например, 
Производные и дифференциалы высших порядков
Производная 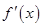 есть сама функция от
есть сама функция от  поэтому можно взять от неё производную. Полученная таким образом функция (если она существует) называется второй производной от функции
поэтому можно взять от неё производную. Полученная таким образом функция (если она существует) называется второй производной от функции  и обозначается
и обозначается  И вообще:
И вообще:
если известна производная  (
( порядка), то производная
порядка), то производная  го порядка определяется так:
го порядка определяется так:  При этом функция
При этом функция  называется
называется  раз дифференцируемой в точке
раз дифференцируемой в точке 
Аналогично определяются дифференциалы высшего порядка. Именно:
если известен дифференциал 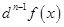
 порядка то дифференциал
порядка то дифференциал  го порядка определяется так:
го порядка определяется так: 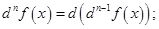 при этом дифференциал
при этом дифференциал  независимой переменной и все его степени
независимой переменной и все его степени  считаются постоянными дифференцирования.
считаются постоянными дифференцирования.
Имеем  И вообще, справедливо утверждение: если функция
И вообще, справедливо утверждение: если функция  дифференцируема
дифференцируема  раз в точке
раз в точке  то
то

Нетрудно доказать следующее утверждение.
Теорема 1. В области определения выписанных ниже функций справедливы равенства:
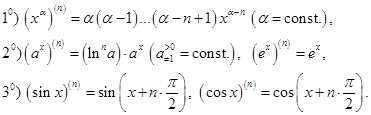

Производные  порядка являются линейными операциями, т.е.
порядка являются линейными операциями, т.е. 
 Производная
Производная  порядка для произведения
порядка для произведения  вычисляется довольно сложно.
вычисляется довольно сложно.
Формула Лейбница. Если функции  дифференцируемы
дифференцируемы  раз в точке
раз в точке  то имеет место равенство
то имеет место равенство

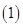
Здесь: 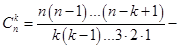 число сочетаний из
число сочетаний из  элементов по
элементов по 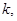 нулевая производная функции
нулевая производная функции  совпадает с ней самой:
совпадает с ней самой:  Легко видеть, что формула (1) напоминает формулу бинома Ньютона; только в ней вместо произведения степеней
Легко видеть, что формула (1) напоминает формулу бинома Ньютона; только в ней вместо произведения степеней  стоит произведение производных
стоит произведение производных  Учитывая это, легко записать, например, третью производную от произведения:
Учитывая это, легко записать, например, третью производную от произведения:

Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
При вычислении пределов функций мы использовали таблицу 1 эквивалентных бесконечно малых. Например, при вычислении предела  мы использовали формулы
мы использовали формулы  Однако этих формул не достаточно для вычисления предела
Однако этих формул не достаточно для вычисления предела


Нужны более точные формулы или так называемые асимптотические разложения высших порядков. Переходя к описанию таких разложений, введём следующее понятие.
Определение 5. Пусть функция  определена в некоторой проколотой окрестности
определена в некоторой проколотой окрестности
точки  Говорят, что функция
Говорят, что функция  имеет в точке
имеет в точке  асимптотическое разложение
асимптотическое разложение  го порядка, если существуют числа
го порядка, если существуют числа  такие, что
такие, что  в некоторой в некоторой проколотой окрестности
в некоторой в некоторой проколотой окрестности  представляется в виде
представляется в виде


Здесь 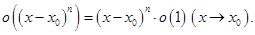 Равенство (3) означает, что функция
Равенство (3) означает, что функция  аппроксимируется (приближённо равна) в некоторой малой окрестности точки
аппроксимируется (приближённо равна) в некоторой малой окрестности точки  многочленом. В каком случае функция
многочленом. В каком случае функция  имеет асимптотическое разложение
имеет асимптотическое разложение  порядка? Ответ на этот вопрос содержится в следующем утверждении.
порядка? Ответ на этот вопрос содержится в следующем утверждении.
Теорема 2. Пусть функция  имеет в точке
имеет в точке  производные
производные  до
до  го порядка включительно. Тогда
го порядка включительно. Тогда  имеет в точке
имеет в точке  асимптотическое разложение
асимптотическое разложение  порядка вида
порядка вида

 (формулу (4) называют формулой Тейлора с остаточным членом
(формулу (4) называют формулой Тейлора с остаточным членом  в форме Пеано или локальной формулой Тейлора).
в форме Пеано или локальной формулой Тейлора).
Если в (4) положить  то получим формулу
то получим формулу  называемую формулой Маклорена-Тейлора. Приведём формулы Маклорена-Тейлора для основных элементарных функций.
называемую формулой Маклорена-Тейлора. Приведём формулы Маклорена-Тейлора для основных элементарных функций.
Теорема 3. Имеют место следующие разложения: 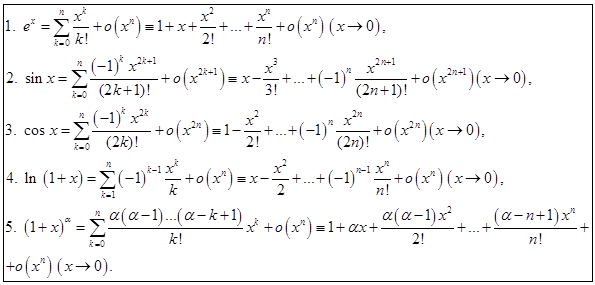
Доказательство этих формул базируется на подсчёте производной  го порядка соответствующей функции. Докажем, например, формулу (2).
го порядка соответствующей функции. Докажем, например, формулу (2).
Итак, пусть  По теореме 1 имеем
По теореме 1 имеем

Значит, в формуле

будут отсутствовать все чётные степени  а слагаемые с нечётными степенями
а слагаемые с нечётными степенями 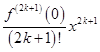 имеют вид
имеют вид  Следовательно имеет место формула 2.
Следовательно имеет место формула 2.
Замечание 1. В формуле 2 остаточный член можно записать в виде  а в формуле 3–
а в формуле 3–
в виде  (почему?).
(почему?).
Теорема 2 аппроксимирует функцию  лишь в достаточно малой окрестности точки
лишь в достаточно малой окрестности точки  Условия представления функции
Условия представления функции  на некотором отрезке
на некотором отрезке  (где
(где  может быть достаточно большим) по формуле Тейлора описаны в следующем утверждении.
может быть достаточно большим) по формуле Тейлора описаны в следующем утверждении.
Теорема 4. Пусть функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1)  существуют и непрерывны на отрезке
существуют и непрерывны на отрезке  ;
;
2) производная 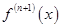 существует и конечна по-крайней мере на интервале
существует и конечна по-крайней мере на интервале 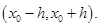
Тогда для всех 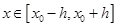 функция
функция  представляется в виде
представляется в виде
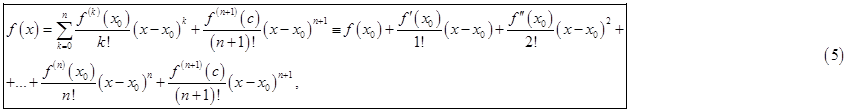 где точка
где точка 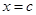 находится между
находится между  и
и 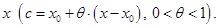
Формулу (5) называют (глобальной) формулой Тейлора с остаточным членом  в форме Лагранжа.
в форме Лагранжа.
Если в формуле (5) положить 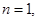 то получим равенство
то получим равенство 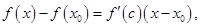 или, обозначая
или, обозначая 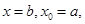 будем иметь
будем иметь



Эту формулу называют формулой Лагранжа. Она верна в случае, когда функция  непрерывна отрезке
непрерывна отрезке 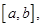 а
а 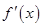 существует и конечна по-крайней мере на интервале
существует и конечна по-крайней мере на интервале  Если,кроме того, выполняется условие
Если,кроме того, выполняется условие  то существует точка
то существует точка 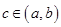 такая, что
такая, что  (теорема Ролля).
(теорема Ролля).






