Функция Лагранжа
.
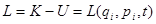Если учесть 
то из определения действия 
- целое кратное 
(
, 
»6.63×10-34 Дж×с – постоянная Планка, или квант действия).
; 
, если 
.
Получим закон сохранения энергии
Воспользуемся уравнениями движения в форме Гамильтона, чтобы получить закон сохранения энергии для простейшей замкнутой системы.
РИС. 2-17
Рассмотрим систему из 2-х частиц, способных двигаться только по направлению 
. Гамильтониан этой системы 
(все аргументы зависят от времени).
Чтобы доказать закон сохранения энергии, нужно убедиться в том, что полная энергия не зависит от времени.
Продифференцируем по времени:
.
Уравнения Гамильтона для этой системы:
.
Подставим:
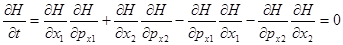, т. е. 
.
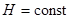Вывод: Полная энергия сохраняется (не зависит от времени).
Финитное и инфинитное движение частицы
РИС. 2-18
Зная вид функции, которой выражается потенциальная энергия, можно судить о характере движения частицы. Если частица при своем движении не может удалиться на бесконечность, это - финитное движение, если двигается как угодно далеко - инфинитное. Пример финитного движения - потенциальная яма, или движение с отрицательной полной энергией в центральном поле сил притяжения.
До сих пор мы всегда относили движение к одной из бесчисленных ИСО, в которых уравнение движения может быть записано или в ньютоновой форме 
, или в гамильтоновой форме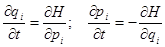 
.
Теперь наша задача состоит в том, чтобы найти уравнения движения в любой инерциальной системе отсчета, т.е. найти законы преобразования ускорений и сил. При этом мы обязаны постулировать:
расстояния и промежутки времени инвариантны по отношению к переходу от одной системы отсчета к другой, произвольно движущейся.
Это справедливо только для малых скоростей движения, когда скорости движения тел в системах и скорости относительного движения систем малы по сравнению со скоростью света в вакууме.
II. Движение в неинерциальных системах отсчета
1. Система 
движется по отношению к системе 
поступательно с некоторой скоростью 
и некоторым ускорением 
.
РИС. 3-1
- радиус-вектор начала системы ,
- радиус-вектор точки 
в системе ,
- радиус-вектор точки в системе .
Очевидно, что в системе (которую считаем неподвижной)
, 
.
Если элементарное перемещение точки в системе есть 
, то это элементарное перемещение складывается из перемещения 
вместе с системой и перемещения 
в системе 
. Поделив на 
, получаем формулу преобразования скоростей:
,
, 
.
Продифференцировав закон преобразования скоростей по времени, получаем закон преобразования ускорений:
, 
.
Сразу видно, что, если 
, т. е. система - инерциальная, то 
.
(Вспомним определения ИСО!)
Умножим в последней формуле правую и левую части на массу частицы 
:
.
Здесь 
- равнодействующая всех сил, действующих на частицу в неподвижной системе отсчета, 
- некая добавочная сила, возникающая только из-за того, что система отсчета является неинерциальной (опять вспомним ИСО - если система отсчета будет двигаться без ускорения, т.е. , то и эта сила =0).
Это - сила инерции:
= - 
.
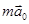Основное уравнение динамики (2-ой закон Ньютона) в неинерциальной системе отсчета: 
2. Система вращается с постоянной угловой скоростью 
вокруг оси, неподвижной в системе .
РИС. 3-2
1)Обе системы отсчета имеют общее начало 
. Радиус-вектор точки будет одним и тем же в обеих системах отсчета: 
.
2) Точка в системе неподвижна. Значит, движение этой точки в системе происходит только за счет вращения системы .
Перемещение: 
Допустим теперь, что точка движется в системе со скоростью 
. Суммарное перемещение этой точки за время будет:
(Здесь первое слагаемое – перемещение за счет движения
точки , второе – за счет вращения системы ).
Поделив на и вспоминая, что 
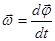, имеем:
– так изменяется скорость.
3) Приращение вектора скорости за время (измеряется в системе ):
- это просто полный дифференциал закона преобразования скоростей.
Приращение вектора скорости за тот же интервал времени в системе :
.
РИС. 3-3
В выражение для 
подставляем и 
:
Поделив на , находим закон преобразования ускорений:
Преобразуем двойное векторное произведение типа 
, пользуясь правилом «бац-цаб»:
, где учтено 
, 
- радиус-вектор, кратчайшим путем соединяющий точку с осью вращения, а также правило сложения векторов.
РИС. 3-4
Итак, 
, 
- осестремительное ускорение,
- кориол и сово (ударение на подчеркнутом «и») ускорение.
Если теперь предположить, что вся неинерциальная система отсчета движется относительно инерциальной с поступательным ускорением , то ускорение точки в инерциальной системе отсчета будет:
для 
,
для 
.
Последнее выражение -
основное уравнение динамики в неинерциальной системе отсчета , вращающейся с постоянной угловой скоростью вокруг оси, перемещающейся с ускорением относительно инерциальной системы .
- инерциальная система, - неинерциальная.
Умножая данное уравнение слева и справа на и учитывая, что в инерциальной системе отсчета , имеем:
, или
,
где
- сила инерции, обусловленная поступательным ускорением системы отсчета ,
- центробежная сила, направлена по нормали! (Рис. 3-4)
- кориол и сова сила; направлена по тангенциальной составляющей!
и 
обусловлены вращением системы отсчета .
Силы инерции зависят от свойств неинерциальной системы отсчета, а также от положения и скорости частицы в данной системе отсчета.
Проявление центробежной силы инерции – уменьшение ускорения свободного падения по мере удаления от полюсов и приближения к экватору, а вот размыв правых берегов рек в северном полушарии (закон Бэра) – пример тангенциональной силы.
РИС. 3-5
Обратите внимание: сила - нормальная к поверхности!
Радиус Земли - 
. Заменим его вместо r.
- на полюсах 
,
на экваторе 
.
, где 
- ускорение свободного падения на полюсах, 
- широта местности.
Задача: поворот плоскости качания маятника Фуко за счет кориол и совой силы. Решение этой задачи французским ученым Фуко в 1852 г. доказало вращение Земли. При колебании маятника на полюсе плоскость его колебаний будет медленно поворачиваться в сторону, противоположную вращению Земли, с угловой скоростью вращения Земли -15 градусов в час. В ИСО плоскость остается неизменной!
. Эта сила направлена вправо по ходу маятника и лежит в горизонтальной плоскости.
РИС. 3-6
Особенности сил инерции
1) Силы инерции действуют только в неинерциальных системах отсчета и обусловлены не взаимодействием тел (как все прочие силы), а свойствами систем отсчета.
2) Силы инерции пропорциональны массе тела, подобно силам тяготения. Следовательно, движение тел в однородном поле сил инерции эквивалентно движению в однородном поле сил тяготения.
Отсюда - принцип эквивалентности Эйнштейна:
в однородном поле сил инерции все физические процессы происходят совершенно так же, как и в однородном поле сил тяготения.
Смысл таков. Допустим, мы не знаем, где находится лаборатория – в космическом пространстве, в невесомости, на Земле, или совершает поступательное движение с некоторым ускорением, или вращается с постоянной угловой скоростью относительно неподвижной оси. Мы замечаем только, что все тела, независимо от их массы, падают с одинаковым ускорением. При этом мы не можем сделать вывод о природе этого явления - вызвано это полем тяготения, или ускоренным движением лаборатории, или обеими этими причинами.
Момент количества движения(момент импульса)
РИС. 3-7
- неподвижное начало отсчета (полюс), - радиус-вектор, 
- импульс.
Моментом количества движения частицы (материальной точки) P относительно некоторой точки называется вектор 
, 
.
Компоненты:
.
Рассмотрим теперь, каким образом и по какой причине момент количества движения (момента импульса) изменяется во времени.
Для этого продифференцируем по времени:
.
Первое слагаемое есть векторное произведение коллинеарных векторов (геометрический смысл: прямые проходящие в направлении векторов параллельны) (
) и поэтому равно нулю: 
.
Во втором слагаемом 
- сумма всех сил, действующих на частицу.
Отсюда 
, 
- момент сил, действующих на частицу,
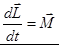- уравнение моментов.
Заметим, что, если система отсчета является неинерциальной, то момент сил включает в себя как момент сил взаимодействия, так и момент сил инерции.
Из уравнения моментов сразу видно, что при 
и, следовательно, 
.
Важное свойство:
Если момент равнодействующей всех сил, действующих на материальную точку, равен нулю относительно некоторой точки и в течение некоторого промежутка времени, то момент количества движения относительно той же точки остается постоянным в течение этого же промежутка времени.
