Мы будем рассматривать два типа преобразования матриц: транспонирование и расчленение. При транспонировании строки матрицы становятся ее столбцами с тем же самым номером. В случае квадратных матриц можно сказать, что транспонирование есть поворот матрицы около главной диагонали. Транспонированная матрица обозначается  .
.
Операция транспонирования имеет свои свойства и следствия.
1. Транспонирование является рефлексивным. Это значит, что транспонирование транспонированной матрицы дает исходную матрицу.
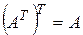
2. Транспонированная сумма матриц равна сумме транспонированных матриц.
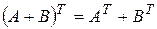
3. Транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.

При расчленении матрица большого размера представляется как матрица, состоящая из некоторого количества матриц меньшего размера. Рассмотрим матрицу А= 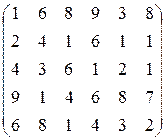 . Введем следующие подматрицы:
. Введем следующие подматрицы:
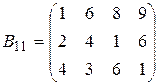 ,
, 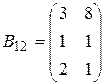 ,
, 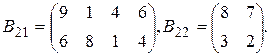
Таким образом, матрицу А можно представить как: 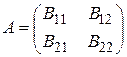
Пример 2. Некоторая компания в обрабатывающей промышленности располагает данными о своих продажах на протяжении года, сгруппированными по видам изготовляемой продукции и районам сбыта. В таблице представлено распределение трех видов продукции по трем районам.
| Виды продукции | Районы продаж | ||
Перепишем содержание таблицы в форме матрицы порядка 3 х 3.

Аналогичные данные, относящиеся к следующему году, можно записать в том же порядке с помощью матрицы В
 .
.
Тогда общее число единиц продукции вида 1, проданной в районе 1 на протяжении рассматриваемых двух лет, равно сумме элементов, расположенных в каждой матрице на пересечении первой строки и первого столбца 98+55=153. Общее число единиц продукции вида 3, проданной в районе 2 за тот же период, равно 15+40=55. Матрица, составленная путем сложения всех указанных величин, будет тогда иметь вид:
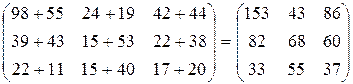
Элементы этой матрицы характеризуют объем продаж различных видов продукции в каждой области на протяжении двух лет.
Пример 3. Пусть существует компания, осуществляющая различные виды продажи товаров. Она имеет разные отделения. В таблице приведены данные о продажах товаров по каждому из отделений.
| Отделение | Виды продукта и его цена | ||
| Вид 1 (1 доллар) | Вид 2 (2 доллара) | Вид 3 (3 доллара) | |
| Розничные продажи | Продано единиц | ||
| Продажи другим фирмам | |||
| Продажи за рубежом |
Содержание этой таблицы можно записать в виде матрицы 
Выручка от продаж по отделениям
| Отделение | Выручка от продаж |
| Розничные продажи | 58*1+26*2+8*3=134 |
| Продажи другим фирмам | 52*1+58*2+12*3=204 |
| Продажи за рубежом | 1*1+3*2+9*3=34 |
Взглянув на эту таблицу легко заметить, что столбец «Выручка от продаж» легко получить как результат произведения матрицы А на матрицу

Такие матрицы, размера 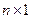 , еще называются вектор - столбцом. Матрицы, размера
, еще называются вектор - столбцом. Матрицы, размера  называются вектор –строкой.
называются вектор –строкой.
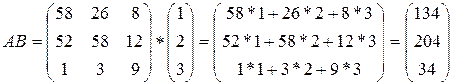
Пример 4. Умножение матрицы на матрицу. Эту операцию можно представить как многократное умножение матрицы на векторы.

Упражнения.
Выполнить действия с матрицами.
1. 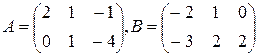 , найти 3А+2B.
, найти 3А+2B.
2. 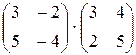 .
.
3. 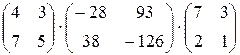 .
.
4.  , найти 3А2-4Е.
, найти 3А2-4Е.
5. 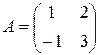 , найти А2-3А+Е.
, найти А2-3А+Е.
6. 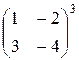
7. 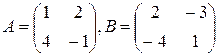 , найти АВ-ВА.
, найти АВ-ВА.
8.  , найти АВ и ВА.
, найти АВ и ВА.
9.  , найти АВ и ВА.
, найти АВ и ВА.
10.  .
.
11.  .
.
12.  , найти А=(В+2С)(В-2Е).
, найти А=(В+2С)(В-2Е).
13. 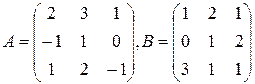 , найти АВ-ВА.
, найти АВ-ВА.
14.  , найти 3А2-2А+5Е.
, найти 3А2-2А+5Е.
15.  , найти А3-7А2+13А-5Е.
, найти А3-7А2+13А-5Е.
Ответы: 1.  . 2.
. 2. 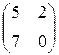 . 3.
. 3. 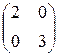 . 4.
. 4.  . 5.
. 5.  .
.
6. 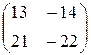 . 7.
. 7.  . 8.
. 8.  , ВА =13. 9.
, ВА =13. 9.  ,
, 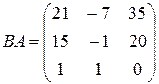 . 10.
. 10.  . 11.
. 11. 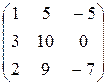 . 12.
. 12.  .
.
13. 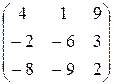 . 14.
. 14. 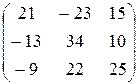 15.
15.  .
.






