Лекция 1. Матрицы. Основные арифметические действия с матрицами. Некоторые другие преобразования матриц.
Матрицей размера  называется прямоугольная таблица,
называется прямоугольная таблица,


состоящая из m строк и n столбцов, элементы которой  принадлежат некоторому множеству К (i – номер строки, j – номер столбца). Мы будем рассматривать множество действительных чисел в качестве множества К. Возможны другие обозначения матрицы
принадлежат некоторому множеству К (i – номер строки, j – номер столбца). Мы будем рассматривать множество действительных чисел в качестве множества К. Возможны другие обозначения матрицы


Матрицы A, B одинаковых размеров  с элементами
с элементами 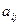 ,
,  называются равными если
называются равными если 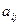 =
=  для i = 1,2 …n, j = 1,2 …m. Равенство матриц обозначается символом A=B.
для i = 1,2 …n, j = 1,2 …m. Равенство матриц обозначается символом A=B.
Матрицы, у которых число столбцов равно числу строк называются квадратными. Общее число строк или столбцов матрицы называется порядком квадратной матрицы. Главной диагональю квадратной матрицы называется диагональ, проходящая через верхний левый и нижний правый углы, т.е. совокупность элементов вида 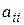 , где i = 1, 2 …,n.
, где i = 1, 2 …,n.
Единичной матрицей Е называется квадратная матрица, у которой элементы  . Она имеет вид:
. Она имеет вид:  .
.
Эта матрица играет роль единицы в операции умножения матриц АЕ=ЕА=А.
Нулевой матрицей О называется матрица, все элементы которой равны нулю.
Некоторые виды матриц.
1) треугольные матрицы – это матрицы, у которых все элементы, расположенные под или над главной диагональю равны нулю.


2) диагональной, называется матрица, у которой на главной диагонали есть элементы не равные нулю, все остальные элементы матрицы равны нулю.
3) симметричной называется квадратная матрица, у которой элементы 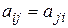 . (Другими словами, это квадратная матрица, в которой все элементы расположены симметрично относительно главной диагонали)
. (Другими словами, это квадратная матрица, в которой все элементы расположены симметрично относительно главной диагонали)
Абсолютная величина и норма матрицы.
Под абсолютной величиной (модулем) матрицы 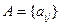 понимается матрица
понимается матрица  , где все элементы
, где все элементы  - модули элементов матрицы A.
- модули элементов матрицы A.
Пусть А и В матрицы, для которых операции А+В и АВ имеют смысл. Тогда
1.  .
.
2.  .
.
3.  .
.
Под нормой матрицы 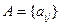 понимается действительное число
понимается действительное число  , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
1.  тогда и только тогда, когда А=0.
тогда и только тогда, когда А=0.
2. 
3. 
4. 
5.  , где А и В матрицы, для которых соответствующие операции имеют смысл.
, где А и В матрицы, для которых соответствующие операции имеют смысл.
Норму матрицы можно определить по-разному. Для матрицы 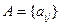 произвольного размера рассмотрим три следующие легко вычисляемые нормы:
произвольного размера рассмотрим три следующие легко вычисляемые нормы:
 - максимальная сумма модулей элементов матрицы по строкам.
- максимальная сумма модулей элементов матрицы по строкам.
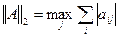 - максимальная сумма модулей элементов матрицы по столбцам.
- максимальная сумма модулей элементов матрицы по столбцам.
 - корень квадратный из суммы квадратов модулей всех элементов матрицы.
- корень квадратный из суммы квадратов модулей всех элементов матрицы.
Пример 1. Для матрицы 
Вычислить все вышеперечисленные нормы матрицы.
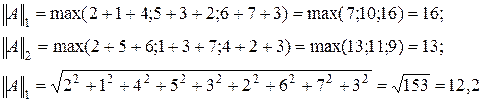
Основные арифметические действия с матрицами.
Суммой двух матриц A и B одинаковых размеров  с элементами
с элементами 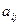 ,
,  называется матрица С тех же размеров с элементами
называется матрица С тех же размеров с элементами  , если
, если  для i = 1,2 …n, j = 1,2 …m. Сумма матриц обозначается символом С=A+B.
для i = 1,2 …n, j = 1,2 …m. Сумма матриц обозначается символом С=A+B.
Разностью двух матриц A и B одинаковых размеров  с элементами
с элементами 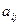 ,
,  называется матрица С тех же размеров с элементами
называется матрица С тех же размеров с элементами  , если
, если 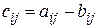
для i = 1,2 …n, j = 1,2 …m. Разность матриц обозначается символом С=A-B.
Произведением матрицы A размеров  с элементами
с элементами 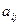 на число
на число  называется матрица С тех же размеров с элементами
называется матрица С тех же размеров с элементами  , если
, если  =
= 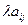 для i = 1,2 …n, j = 1,2 …m. Произведение матрицы на число обозначается символом С=
для i = 1,2 …n, j = 1,2 …m. Произведение матрицы на число обозначается символом С=  A.
A.
Произведением матрицы A размеров n  m c элементами
m c элементами  и матрицы B размеров m
и матрицы B размеров m  p с элементами
p с элементами  и, называется матрица С размеров n
и, называется матрица С размеров n  p с элементами
p с элементами 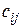 , если
, если  , для i = 1,2 …n, j = 1,2 …p. Произведение матриц обозначается символом С=AB.
, для i = 1,2 …n, j = 1,2 …p. Произведение матриц обозначается символом С=AB.
Таким образом, произведение определено лишь для тех матриц, у которых число столбцов левого сомножителя равно числу строк правого сомножителя. Такие матрицы называют согласованными. Элемент матрицы произведения, стоящий на пересечении i-ой строки и j-го столбца, равен сумме произведений всех элементов i-ой строки левого сомножителя на соответствующие элементы j-го столбца правого сомножителя.
Следствием этого правила является тот факт, что произведение  существует только в том случае, если матрица А – квадратная. Матрица
существует только в том случае, если матрица А – квадратная. Матрица 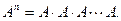 называется n-ой степенью матрицы A.
называется n-ой степенью матрицы A.
Другое следствие этого правила: произведения АВ и ВА существуют во всех тех случаях, когда А и В представляют собой квадратные матрицы одинакового порядка. О произведении АВ двух матриц А и В будем говорить, что матрица В умножается на матрицу А слева или что матрица А умножается на матрицу В справа. Произведение нескольких матриц АВС следует понимать так: матрица А умножается справа на матрицу В, а полученная матрица умножается на матрицу С справа. В общем случае умножение матриц не коммутативно, другими словами АВ не всегда равно ВА. Несоблюдение закона коммутативности при умножении матриц можно продемонстрировать с помощью следующего примера:

В отдельных же случаях матрицы АВ и ВА равны:

Любая матрица А, умноженная слева или справа на нулевую матрицу соответствующего размера, дает нулевую матрицу,






