Рассмотрим обобщённый метод определения запусков на технологические операции с использованием линейных сетевых стохастических моделей производственных систем.
Допустим, Nj – суммарная интенсивность потока требований (количество заготовок) в системе j (запуск на j-ю операцию); N0- интенсивность предыдущего производственного участка или склада заготовок; Nm- интенсивность последующего производственного участка или склада готовой продукции (выпуск линии). Если процесс стационарен (т. е. установившийся режим), то
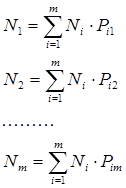
или, используя матричную запись,
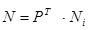
где PT – транспонированная матрица Р
Тогда для получения значений запусков на каждую операцию Nj необходимо решить следующую систему линейных однородных уравнений с (m+1) неизвестными(включая N0):
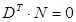, (1)
где DT – матрица, транспонированная по отношению:
D = P – I, (2)
где I – единичная матрица.
Если Nm известно (задано):
Nm=П, (3)
где П – план выхода годных изделий с линии, то в соответствии с теоремой Кронекера-Капелли система (1) может иметь нулевое единственное решение, если при N≠0 иусловии (3) det DT =0, а ранг матрицы DT был равен в точности m.
Решение задачи по варианту
В соответствии с алгоритмом метода расчета построим топологическую модель технологического процесса в виде линейной стохастической сети, на которой коэффициенты выхода после каждой технологической операции представлены весами дуг этой модели.
План выхода годных изделий/смену П=1000 шт/смену.
Из равенства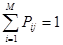 
найдём недостающие коэффициенты выхода после технологической операции.
Структуры технологических процессов производства печатных плат
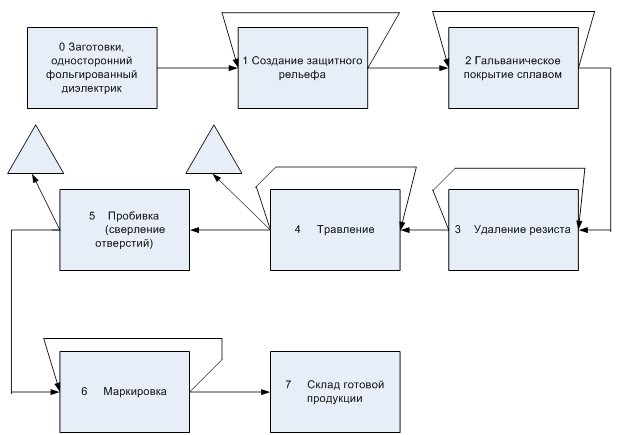
Рис. 4 Структура технологического процесса (ТП) изготовления односторонних печатных плат субтрактивным негативным методом
Коэффициенты выхода для ТП, изображенного на рис. 4.
| Kij | Варианты | |
| i | j | |
| 0.9 | ||
| 0.75 | ||
| 0.8 | ||
| 0.01 | ||
| 0.9 | ||
| 0.85 | ||
| 0.95 | ||
| План выхода годных (шт/смену) |
Граф передач технологического процесса (линейная стохастическая сеть).
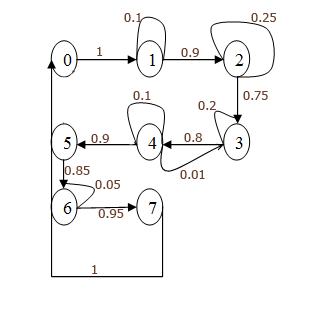
Составим матрицу передач участка фотолитографии:
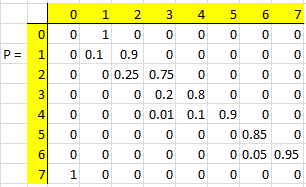
Построим матрицу D = P – I:
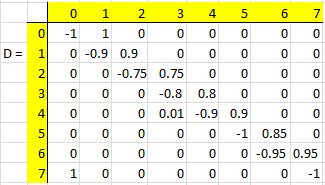
Составим транспонированную матрицу Dт, т.е. заменим строки матрицы D ее столбцами с сохранением их номеров:
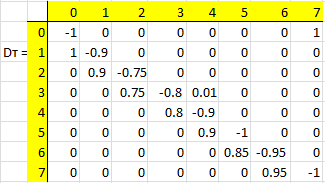
Запишем систему линейных однородных уравнений:
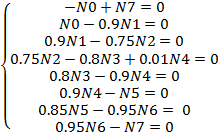
Решая систему уравнений при N7 =1000 шт/смену, получаем величины запусков на все технологические операции участка фотолитографии:
· на операции снятия фоторезиста
N0 = 0.9N1 = 1163 шт/смену;
· на операции травления
N1 = 0.75N2/0.9 = 1292 шт/смену;
· на операции термического задубливания
N2 = 0.8N3 – 0.01N4/0.75 = 1551 шт/смену;
· на операции проявления
N3 = 0.9N4/0.8 = 1470 шт/смену;
· на операции совмещения и сушки
N4 = N5/0.85 = 1307 шт/смену;
· на операции нанесения фоторезиста
N5 = 0.95N6/0.85 = 1176 шт/смену;
· интенсивность источника (выпуск с участка диффузии)
N6 = N7/0.95 = 1052 шт/смену.
Как видно из полученных результатов, запуск на операции травления больше, чем на операции снятия фоторезиста (N1 >N0). Это объясняется тем, что на эту операцию поступают заготовки с последующих операций.
