Знайдіть координати вершини параболи.

Підсумкова контрольна робота з алгебри

У 9-х класах

Пропонуються 20 варіантів. Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.

У І частині контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки один правильний. Завдання вважається виконаним правильно, якщо учень указав тільки одну літеру, якою позначений правильний варіант відповіді. Правильна відповідь за кожне із завдань 1-5 – оцінюється одним балом.

ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис рішення без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.

ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис рішення з обґрунтуванням. Правильне розв’язання завдання цього блоку оцінюється трьома балами.

Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожного блоку (5; 4; 3-всього 12балів).

Учні загальноосвітніх класів виконують всі завдання крім завдання з позначкою «м».

Учні, які навчаються в класах з поглибленим вивченням математики виконують всі завдання І-ІІ частин, з ІІІ частини-тільки завдання з позначкою «м».

Учні загальноосвітніх класів виконують всі завдання крім завдання з позначкою «м».

Учні, які навчаються в класах з поглибленим вивченням математики, виконують всі завдання І-ІІ частин, а з ІІІ частини- тільки завдання з позначкою «м»

Контрольна робота розрахована на 45 хвилин. Роботи виконуються у зошитах або на окремих аркушах. При виконанні роботи необхідно вказати номер завдання. Текст завдань переписувати не обов’язково.

Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності

Варіант 1

І частина (5 балів)

Завдання 1- 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть правильну відповідь. Правильна відповідь кожного завдання оцінюється одним балом.

№1. Оцініть периметр правильного трикутника зi стороною a см, якщо
2,1< a < 2,3.

А) 6,3< Р <6,9; Б) 6,3< Р <2,3; В) 2,1< Р <6,9; Г) 4,1< Р <4,6.

№2. Який з числових проміжків є розв’язком подвійної нерівності ?

А) В)

-4 1 x -4 1 x

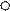
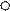
Б) Г)

-4 1 x -4 1 x

№3. Скільки відсотків години складає 18 хвилин?

А) 30%; Б) 10,8%; В) 20%; Г)10%.

№4. Яка пара чисел є розв’язком системи рівнянь ?

А) (–3; 4); Б) (5; – 4); В) (4; 3); Г) (–5; 4).

№5. У скриньці 5 чорних і 7 білих кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька біла.

А) 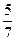; Б) ; В) ; Г) .

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Правильне рішення кожного завдання оцінюється двома балами.

№6. Побудувати графік функції у = х ² – 2 х – 3. За графіком визначити:

а) значення у, якщо х = – 1,5;

б) значення х, якщо у = 5;

в) нулі функції.

№7. Знайдіть сьомий член і суму чотирнадцяти перших членів арифметичної прогресії, якщо перші чотири члени дорівнюють: 2; 6; 10; 14.

ІІІ частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

№8. Відстань між двома містами дорівнює 93 км. З одного міста в друге виїхав велосипедист, швидкість якого була на 3 км/год більша за швидкість першого. Велосипедисти зустрілись на відстані 45 км від першого міста. Знайдіть швидкість кожного велосипедиста.

№8^м Два спортсмени біжать по одній замкнутій доріжці стадіону. Швидкість кожного постійна, але перший пробігає всю доріжку на 10 с швидше, ніж другий. Якщо вони почнуть біг із спільного старту в одному напрямку, то ще раз зустрінуться через 720 с. Яку частину довжини всієї доріжки пробігає за секунду кожний спортсмен?

Варіант 2

І частина (5 балів)

№1. Оцiнiть периметр квадрату зi стороною b см, якщо 0,4< b <0,7.

А) 0,8< P <1,4; Б) 1,6< P <2,8; В) 1,2< P <2,1; Г) 0,4< P <2,8.

№2. Який з числових проміжків є розв’язком подвійної нерівності ?

А) В)

-1 4 x -1 4 x

Б) Г)

-1 4 x -1 4 x

№3. Скільки відсотків години складає 42 хвилини?

А) 70%; Б) 25,2%; В) 60%; Г) 14,2%.

№4. Яка пара чисел є розв’язком системи рівнянь ?

А) (10;-9); Б) (11; 10); В) (10; 9); Г) (9; 10)

№5. У скриньці 6 червоних і 5 синіх кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька синя.

А) 0; Б) ; В) ; Г) .

ІІ частина (4 бали)

№6. Побудувати графік функції у = х ²+ 2 х – 3. За графіком визначити:

а) значення у, якщо х = – 1,5;

б) значення х, якщо у = 5;

в) нулі функції.

№7. Знайдіть шостий член і суму дванадцяти перших членів арифметичної прогресії, якщо відомі перші чотири члени: 4; 8; 12; 16.

ІІІ частина (3 бали)

№8. Із села А в село В, відстань між якими дорівнює 30 км, велосипедист проїхав з певною швидкістю, а повертався зі швидкістю на 3 км/год більшою і витратив на 30 хв менше, ніж на шлях з села А в село В. Знайдіть початкову швидкість велосипедиста.

№8^м Пароплав відходить від відстані А на припливі, йде вниз за течією 80км до ріки, далі по річці нагору проти течії до пристані В,затративши на весь шлях від А до В 18 год. Потім пароплав повертається назад. Час зворотного руху від В до А по тому ж шляху дорівнює 15год. Власна швидкість пароплава дорівнює 18км/год. Швидкість течії ріки 3км/год. Знайдіть відстань від пристані А до В і швидкість припливу.

Варіант 3

І частина (5 балів)

№1. Розв'яжіть систему нерівностей

А) (9;10); Б) (10;+ ∞); В) (– ∞;10); Г) (9;+ ∞).

Знайдіть координати вершини параболи.

А) ; Б) ; В) ; Г) .

№3. Із свіжих груш отримують 18% сушених. Скільки взяли свіжих груш, якщо отримали 9 кг сушених?

А) 50 кг; Б) 500 кг; В) 200 кг; Г)20 кг.

№4. Відриваємо один аркуш у новому відривному календарі високосного року. Яка з наведених подій є вірогідною?

А ) на аркуші 1 вересня; Б) на аркуші число, яке менше за 32;

В) на аркуші 31 червня; Г) відірваний аркуш - вихідний день.

№5. Знайдіть медіану вибірки 9; 17; 26; 7; 14.

А) 17; Б) 14,6; В) 14; Г) 7.

ІІ частина (4 бали)

№6. Розв’яжіть систему нерівностей .

№7. Знайдіть чотири числа, що утворюють геометричну прогресію, якщо перший член більший від третього на 6, а другий менший від четвертого на 3.

ІІІ частина (3 бали)

№8. Із пункту А до пункту Б, відстань між якими 5 км, вийшов пішохід, а через 30 хв. слідом за ним виїхав велосипедист, швидкість якого на 10 км/год більша від швидкості пішохода. До пункту Б велосипедист приїхав на 10 хв. раніше від пішохода. Знайдіть швидкість велосипедиста і пішохода.

№8^м З пункту А і В,розташованих на відстані 100км, назустріч один одному одночасно виїхали два велосипедисти. Через 4 год вони зустрілися. Після зустрічі швидкість першого велосипедиста, що рухався з А до В, зросла на 5 км/год, а швидкість другого – на 10 км/год. Знайдіть початкову швидкість другого велосипедиста, якщо перший прибув до пункту В на 1год раніше, ніж другий – до пункту А.

Варіант 4

І частина (5 балів)

№1. Розв'яжіть систему нерівностей

А) (1;8); Б) (8;11); В) (- ;8); Г) (1; + ).