Умножение с ПТ. Схема и алгоритм умножения мантисс, начиная со старших разрядов множителя и со сдвигом множимого
Умножение мантисс
Умножение происходит с округлением.
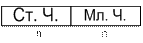
1) Можно просто отбрасывать младшую часть.
2) Если 1, то к старшей части прибавляется 1, если 0, то не прибавляется.
Порядки
Е3 – смещенный порядок произведения.
Е3=Е1+Е2-D
В – смещение; D=16383
Е1=Еист1+D E2=Eист2+D
Поэтому нужно одно смещение вычесть.
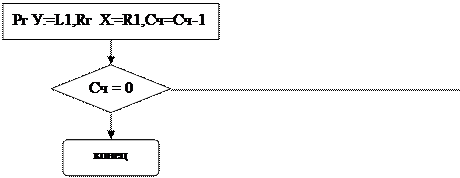
Если сомножитель равен нулю, то и произведение равно нулю.
Переполнение мантиссы
1. хх…х 1.юююн
Можем получить:
10.
11.
Поэтому нужно предусмотреть сдвиг влево, чтобы не терять 1 бит.
При переполнении мантиссы она сдвигается на 1 бит вправо, а к порядку произведения прибавляется 1.
0.1х…х
0.1х…х
Можем получить 0.01…
Если необходимо нормализовать, то необходим сдвиг влево на 1 бит и из порядка вычитается 1.
Порядки
Может быть переполнение порядков
Плюс умножения с ПТ: числа в прямом коде, не нужно преобразовывать в ДК, как это нужно с целыми числами
 |  |
Y n X n

|

|
 |  | ||||||
 |  | ||||||
0,1
 | |||
 |
2n
 |






См ЧП


 2n
2n
|
 2n
2n

 |

 нет
нет
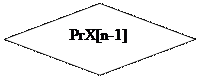 1
1
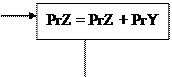 |
 0
0
 | |||
 |
Умножение с ПТ. Схема и алгоритм умножения мантисс, начиная с младших разрядов множителя и со сдвигом множимого.
Умножение мантисс
Умножение происходит с округлением.
3) Можно просто отбрасывать младшую часть.
4) Если 1, то к старшей части прибавляется 1, если 0, то не прибавляется.
Порядки
Е3 – смещенный порядок произведения.
Е3=Е1+Е2-D
В – смещение; D=16383
Е1=Еист1+D E2=Eист2+D
Поэтому нужно одно смещение вычесть.
Если сомножитель равен нулю, то и произведение равно нулю.
Переполнение мантиссы
1. хх…х 1…y
Можем получить:
10.
11.
Поэтому нужно предусмотреть сдвиг влево, чтобы не терять 1 бит.
При переполнении мантиссы она сдвигается на 1 бит вправо, а к порядку произведения прибавляется 1.
0.1х…х
0.1х…х
Можем получить 0.01…
Если необходимо нормализовать, то необходим сдвиг влево на 1 бит и из порядка вычитается 1.
Порядки
Может быть переполнение порядков
Плюс умножения с ПТ: числа в прямом коде, не нужно преобразовывать в ДК, как это нужно с целыми числами
 |  |
Y n X n

|

|
 |  | ||||||
 |  | ||||||
0,1
 | |||
 |
2n
 |






См ЧП


 2n
2n
|
 2n
2n

 |

 нет
нет
 1
1
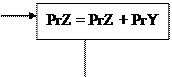 |
 0
0
 | |||
 |
Умножение с ПТ. Схема и алгоритм умножения мантисс, начиная со старших разрядов множителя и со сдвигом суммы частных произведений.
Умножение мантисс
Умножение происходит с округлением.
5) Можно просто отбрасывать младшую часть.
6) Если 1, то к старшей части прибавляется 1, если 0, то не прибавляется.
Порядки
Е3 – смещенный порядок произведения.
Е3=Е1+Е2-D
В – смещение; D=16383
Е1=Еист1+D E2=Eист2+D
Поэтому нужно одно смещение вычесть.
Если сомножитель равен нулю, то и произведение равно нулю.
Переполнение мантиссы
1. хх…х 1…y
Можем получить:
10.
11.
Поэтому нужно предусмотреть сдвиг влево, чтобы не терять 1 бит.
При переполнении мантиссы она сдвигается на 1 бит вправо, а к порядку произведения прибавляется 1.
0.1х…х
0.1х…х
Можем получить 0.01…
Если необходимо нормализовать, то необходим сдвиг влево на 1 бит и из порядка вычитается 1.
Порядки
Может быть переполнение порядков
Плюс умножения с ПТ: числа в прямом коде, не нужно преобразовывать в ДК, как это нужно с целыми числами
 |  |
 Y n X n
Y n X n
|

|
 | |||||
 |  | ||||
0,1
 | |||
 |
n
 |






См ЧП

 n
n
 2n-1 n n-1 0
2n-1 n n-1 0
 |
 2n
2n

 |

 нет
нет
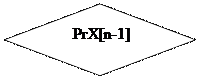 1
1
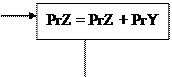 |
 0
0
 | |||
 |






