Программирование в среде MATLAB
Написать файл-функцию с использованием операторов ветвления и циклов, на основании вариантов задания. Вывести в командное окно исходные и расчётные данные, используя команды форматного вывода.
Варианты заданий.
1. Найти произведение отрицательных элементов массива.
2. Подсчитать количество «единиц», стоящих на чётных местах массива.
3. Найти сумму положительных элементов массива, стоящих на местах, кратных 5.
4. Найти сумму элементов массива, больших 5, стоящих на местах кратных трём.
5. Найти сумму отрицательных элементов массива, расположенных на нечётных местах.
6. Найти произведение элементов массива, больших или равных 2.
7. Найти сумму последних пяти элементов массива, меньших 5.
8. Среди n первых элементов массива найти сумму отрицательных элементов.
9. Найти сумму и количество элементов массива, больших единицы.
10. Подсчитать количество элементов массива, попавших в интервал [a,b].
11. Найти первый отрицательный элемент массива, вывести его номер и значение.
12. Найти количество элементов массива, меньших единицы.
13. Найти количество нулевых элементов массива среди последних 5-и его элементов.
14. Найти произведение ненулевых элементов массива.
15. Найти произведение положительных элементов массива, расположенных на нечётных местах.
16. Заменить отрицательные элементы вектора суммой модулей всех его отрицательных элементов.
17.Заменить положительные элементы вектора суммой вех его отрицательных элементов.
18. Заменить максимальный элемент вектора средним значением всех его элементов.
19. Вычислить произведение элементов вектора, не превосходящих среднее арифметическое значение модулей его элементов.
20. Для заданного вектора найти наибольшее значение и вычесть его из всех элементов вектора. Вывести исходный и преобразованный вектора.
21. Для заданного вектора найти наименьшее значение и прибавить его ко всем элементам вектора. Вывести исходный и преобразованный вектора.
22. Для заданного вектора найти наибольшее значение и умножить на него все элементы вектора. Вывести исходный и преобразованный вектора.
23.. Для заданного вектора найти наименьшее значение и умножить на него все элементы вектора. Вывести исходный и преобразованный вектора.
24. Для заданного вектора найти наибольшее значение и разделить на него все элементы вектора. Вывести исходный и преобразованный вектора.
25.. Для заданного вектора найти наименьшее значение и разделить на него все элементы вектора. Вывести исходный и преобразованный вектора.
26. Найти сумму элементов массива, больших 5, стоящих на местах кратных трём.
27. Среди n первых элементов массива найти сумму отрицательных элементов.
28. Найти первый отрицательный элемент массива, вывести его номер и значение.
Простые вычисления.
Вывести графики заданных функций одновременно на одном графике в декартовых координатах (plotyy). Для разных графиков использовать разный тип и цвет линий. Графики необходимо подписать.
Варианты заданий:
| № | Функция 1 | Функция 2 | a | b | h |
| y1 = sin(x) | y2 = exp(x+3)/5000 – 1 | -2π | 2π | π/20 | |
| y1 = cos(x) | y2 = 0.00025e3–x – 0.6 | -2π | 2π | π/20 | |
| y1 = |tg(x)| + 0.1 | y2 = (1+x)6 | -2π | 2π | π/20 | |
| y1 = (x2–1)/15 | y2 = 1+sin(x) | -2π | 2π | π/20 | |
| y1 = (x3–2)/15 | y2 = 5cos(x) | -2π | 2π | π/20 | |
| y1 = x2 – 10 | y2 = 0.025exp(–1.2x) | -5 | 0,2 | ||
| y1 = 3sin(x) | y2=0.015x3 | -5 | 0,2 | ||
| y1 = 4sin(x) | y2 = 0.05x2 | 0,2 | |||
| y1 = 6sin(x) | y2 = 0.01x3 | -10 | 0,1 | ||
| y1 = 2+cos(x) | y2 = – 0.05(x2 + 10cos(x)) | -8 | 0,1 | ||
| y1 = sin2(x/3) | y2 = 0.01(x2 – 40sin(x)) | -8 | 0,1 | ||
| y1 = cos3(x) | y2 = sin(x) + sin(2x) | -π | π | π/8 | |
| y1 = 0.5x + cos2(x) | y2 = sin2(x) + cos(x) | -π | π | π/8 | |
| y1 = sin(x) + cos2(2x) | y2 = x(0.5 + x)exp(0.1x) | -π | π | π/8 | |
| y1 = |sin(x)|*exp(x/2) | y2 = 5x – sin(x) | 0.1 | |||
| y1 = sin(x) | y2 = 5cos3(x) | 2π | 0,1 | ||
| y1 = sin(x) | y2 = 10cos(x) | 2π | 0,1 | ||
| y1 = exp(–x) cos(10x) | y2 = exp(–x) sin(10x) | 2π | 0.03 | ||
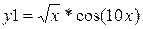
| y2 = exp(–x) sin(10x) | 0.03 | |||
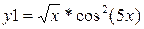
| 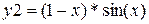
| 0.03 | |||
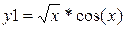
| 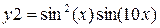
| 0.03 | |||
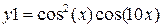
| 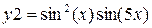
| 0.03 | |||
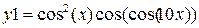
| 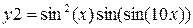
| 2π | 0.03 | ||
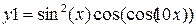
| 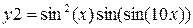
| 2π | 0.01 | ||
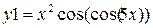
| 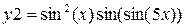
| 2π | 0.01 | ||
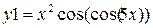
| 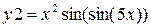
| 2π | 0.01 | ||
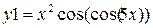
| 
| 2π | 0.01 | ||
| y1 = cos3(x) | y2 = sin(x) + sin(2x) | -π | π | π/8 |
Многомерные вычисления
Вывести функцию в виде графиков в подокнах общего окна:
a) трехмерный с аксонометрией, функция plot3 (X,Y,Z);
b) трехмерный с функциональной окраской, функция mesh (X,Y,Z);
c) трехмерный с функциональной окраской и проекцией, функция meshc (X,Y,Z);
d) трехмерный с функциональной окраской и проекцией, функция surf (X,Y,Z).
Используя команды оформления графиков, нанести дополнительную информацию. С помощью команды colorbar установить соответствия между цветом и значениями функции. При построении графиков использовать координатную сетку.
Варианты заданий:
| № | Функция | Пределы изменения | |
| x,y | шаг | ||
| z=sin(x)*cos(y) | [-2π; 2π] | π/8 | |
| z=sin(x/2)*cos(y) | [-2π; 2π] | π/8 | |
| z=sin(2*x)*cos(y) | [-2π; 2π] | π/10 | |
| z = sin(x)*cos(y/2) | [-2π; 2π] | π/10 | |
| z = sin(x/2)*cos(2y) | [-2π; 2π] | π/10 | |
| 6 | z = sin(2*x)*cos(2y) | [-2π; 2π] | π/8 |
| 7 | z = (1+sin(x))*(sin(y)) | [-2π; 2π] | π/10 |
| z = (sin(x))*cos(y) | [-2π; 2π] | π/8 | |
| z = (sin(x))*|cos(y)| | [-2π; 2π] | π/10 | |
| z = (sin(x))*y | [-2π; 2π] | π/12 | |
| z = (sin(x))*|y| | [-2π; 2π] | π/10 | |
| z = (sin(x))*sin(y) | [-2π; 2π] | π/16 | |
| z = (sin(x))*|sin(y)| | [-2π; 2π] | π/12 | |
| z = (sin(x))*(1+y) | [-2π; 2π] | π/8 | |
| z = (sin(x))*|y+0.5| | [-2π; 2π] | π/10 |
Решение уравнений
Решение системы из двух нелинейных уравнений.
1.Создать Mat–функции для функций f 2(x) и f 3(x) = f 1(x) - f 2(x).
2.Вывести f 1(x) и f 2(x) в виде XY графиков в одном графическом окне. Определить приближенно корни системы уравнений, как координаты точек пересечения графиков f 1(x) и f 2(x). Если корни на графике не просматриваются, то изменить пределы изменения аргумента и повторить операции.
3.Для каждого корня найти точное значение, используя функцию fzero к переменной f3(x). Отметить корни на графике маркерами произвольного вида и цвета. Подписать корни соответствующими им значениями.
4.Сформировать строку с результатами и вывести ее в заголовок окна графика.
Варианты заданий:
| № варианта | 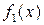 – полином 3-ей степени с коэффициентами ai – полином 3-ей степени с коэффициентами ai
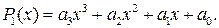
| 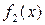
| |||
| a 3 | a 2 | a 1 | a 0 | ||
| -1 | -1 | 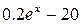
| |||
| -2 | -15 | 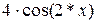
| |||
| -1 | 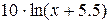
| ||||
| -8 | -70 | 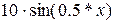
| |||
| -4 | 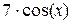
| ||||
| -5 | 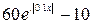
| ||||
| -3 | 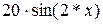
| ||||
| -6 | 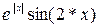
| ||||
| -9 | 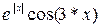
| ||||
| -7 | 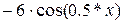
| ||||
| -1 | -4 | 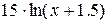
| |||
| -2 | -6 | -7 | 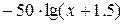
| ||
| -3 | -9 | -8 | 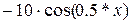
| ||
| -4 | -75 | 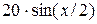
| |||
| -5 | -1 | 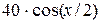
|
Учреждение образования
Белорусский государственный университет
информатики и радиоэлектроники
Кафедра систем управления
Индивидуальная работа
по курсу
«Учебная практика»
Выполнил:
Студент гр.
Проверил:
Минск, 2012






