Модальная и темпоральная логикИ
Модальная логика восходит к начатым Аристотелем исследованиям утверждений, содержащих слова: «неизбежно» и «возможно». В действительности модальностями такого вида богаты и человеческий, и научный языки, например: «обязательно» и «допустимо», «всегда» и «иногда». Поэтому проблемы модальной логики интересовали математиков всегда. Модальная логика перенесла бурное развитие в 60-х годах ХХ века, благодаря методу интерпретации модальностей с помощью моделей Крипке.
Темпоральная логика изучает высказывания, содержащие слова, связанные со временем, например: «будет всегда» и «произойдёт», «завтра» и «вчера». Её основатель – Артур Прайер.
В 80-х годах ХХ века интерес к модальной логике повысился в связи с новым подходом к алгоритмической логике Хоара, применяемой для доказательства правильности программ. Этот подход был основан Воганом Праттом, предложившим рассматривать каждую программу как особый вид модальности.
Синтаксис модальной логики
Фиксируется бесконечное счётное множество Р. Элементы из Р называются простымивысказываниями, или (пропозициональными) атомами, и обычно обозначаются через p, q, r, или p1, p2, p3, …. (Модальные) формулы строятся из атомов и символа 1 («истина») с помощью логических связок & и Ø, и модальности 
(«квадрат») по индукции:
1) каждый атом p Î P является формулой;
2) символ 1 является формулой;
3) если A и B – формулы, то ØA, A & B, A – формулы;
4) каждая формула построена по этим трём правилам.
Темпоральные формулы используют вместо символа квадрата символы: [F] и [P] (будущего и прошлого). Вместо А применяется запись: [F]A или [P]A. Для образования темпоральных формул применяются правила 1, 2, 4 и правило:
3¢) если А и В – формулы, то ØA, A & B, [F]A и [P]A – формулы.
Дополнительные логические связки
Символ 0 (ложь) и связки Ú, ®, «введём как сокращенные записи операций:
0 = Ø1, А Ú В = Ø(ØА & ØВ), А ® В = Ø(ØА &ØВ), А «В = (А ® В) & (В ® А). Положим: àА = Ø ØА для модальности. В случае темпоральных формул введём сокращения: <F>A = Ø[F]ØА и <P>A = Ø[P]ØА. В некоторых случаях сокращения 0, Ú и à будут использоваться как самостоятельные символы.
Замечание. Обычно вместо [F]А и [P]А применяется запись: GA и HA соответственно. В этом случае вместо <F>A и <P>A пишут: FA и PA.
Приоритеты операций
С целью уменьшения количества скобок будем предполагать, что приоритеты унарных связок выше, чем приоритеты бинарных и располагаются в порядке убывания следующим образом:
Ø, , à, [F], [P], <F>, <P>, &, Ú, ®, «.
Для унарных операций взаимные приоритеты не имеют значения (и могут считаться равными). Например, àА & ØВ ® С означает: (((àА) & ( (ØВ))) ® С).
Смысловые значения модальностей
Уточним, что мы понимаем под символами: , à, [F], [P], <F>, <P>. Значения этих символов зависят от области применения и могут обладать неодинаковыми свойствами. Например, А = «А обязательно», àА = «А возможно» обладают свойством А ® А («Если сегодня в Москве обязательно идёт дождь, то в Москве идёт дождь»). А модальности А = «необходимо А», àА = «допустимо А» не обладают этим свойством. Например, высказывание: «Если необходим дождь, то идёт дождь» – может быть ложным.
Другие значения модальностей: А = «А известно» и àА = «А предположительно», А = «А всегда верно» и àА = «А иногда верно». При доказательстве правильности программ используются модальности А = «после окончания работы программы будет верно А» и àА = «программа может закончиться так, что А станет верным». Темпоральные связки в зависимости от области применения могут принимать значения: [F]А = «А будет всегда верно», <F>А = «А будет верно в некоторый момент»; или
[F]А = «А будет верно всегда, начиная с этого момента времени», <F>А = «А верно сейчас или будет верно потом». Значения [P]А и <P>А определяются симметрично к [F]А и <F>А и относятся к прошедшему времени. Связки «завтра» и «вчера», «до тех пор, пока не» и «с тех пор, как» будут определены позже.
Заметим, что , [F], [P] похожи на квантор всеобщности, а à, <F>, <P> – на квантор существования.
Примеры
Рассмотрим смысловые значения формул модальной логики:
А = «известно, что А известно»;
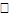àА = «необходимо, чтобы А было допустимо»;
А ® А = «если известно, что А верно, то А – верно»;
[P][P]А ® [P]А = «если всегда было верно, что А было верно всегда, то А всегда было верно»;
А ® А = «если известно, что А известно, то А известно»;
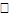А ® 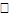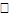А = «если агент знает А, то он знает, что он знает А»;
А ® [F]<P>А = «если А верно, то в будущем всегда будет верно, что в некоторый момент прошлого было верно А»;
àØ<P>А = «возможно, что А не было верным никогда»;
А & В ® (А & В) = «если А и В известны, то известно А & В».
