Распределение Баллов по аттестациям
| № п/п | Наименование работы | Содержание работы | Баллы | Срок выполнения |
| Математическая модель линии электропередач | Расчетная работа выполняется в Mathcad | 6.02.2013 | ||
| Математическая модель силового трансформатора | Расчетная работа выполняется в Mathcad | 20.02.2013 | ||
| Расчет установившегося режима работы СЭС | Расчетная работа выполняется в Mathcad | 20.03.2013 | ||
| Расчет устойчивости СЭС | Расчетная работа выполняется в Mathcad | 03.04.2013 | ||
| Тест «Математические модели элементов СЭС» | Тест в системе Educon | 20.03.2013 | ||
| Тест «Математические модели СЭС» | Тест в системе Educon | 17.04.2013 | ||
| Итоговый тест | Тест в системе Educon | 24.04.2013 | ||
| Поощрения | Работа на занятиях, индивидуальные задания | В течение семестра | ||
| ИТОГО |
Расчётная работа 1.
Математическая модель линии электропередач
Цель работы:
- изучить схемы замещения линий электропередач;
- изучить математические модели различных схем замещения линий электропередач;
- научиться определять основные параметры линий электропередач;
Основные теоретические положения:
Модель линии электропередач (ЛЭП) можно представить как четырехполюсник (рис. 1).
Рис. 1. Четырехполюсник
Тогда, система уравнений четырехполюсника [Бессонов]
(1)
Здесь
,
где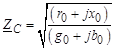 
– волновое сопротивление линии;
– коэффициент распространения волны;
α0 – коэффициент затухания волны;
β0 – коэффициент фазы;
r0 – справочное активное сопротивление линии, Ом/км;
х0 - справочное реактивное (индуктивное) сопротивление линии, Ом/км;
b0 – справочная реактивная проводимость линии, См/км;
g0 – активная проводимость линии, Ом/км; g0 = b0 tgδ;
tgδ – тангенс диэлектрических потерь (принять 0,5%).
Изменение напряжение и тока вдоль линии описывается системой уравнения вида 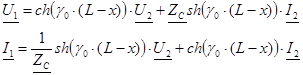(2)
(2)
На практике чаще используется П-образная схема замещения ЛЭП (рис. 2).
Рис. 2. П-образная схема замещения ЛЭП
Уравнения, описывающие П-образную схему замещения, приведены в виде системы (3)
(3)
где
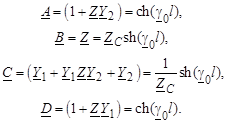
Для исследования режимов работы ЛЭП сверхвысокого напряжения используют уравнения идеальной линии, когда r 0 = 0, g 0 = 0.
(4)
Для исследований коротких ЛЭП сверхвысокого напряжения используется упрощенная модель, описываемая уравнениями (5)
(5)
Г-образная схема замещения ЛЭП используется для моделирования очень коротких линий. Система уравнений, описывающая данную математическую модель, соответствует системе 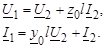(6)
(6)
Коэффициенты четырехполюсника моделей ЛЭП
| Модель | A | B | C | D |
| Уравнения длинной линии | 
| 
| 
|
|
| Уравнения идеальной линии | 
| 
| 
|
|
| Модель с сосредоточенными параметрами П-образной схемы замещения | 
| 
| 
|
|
| Модель с сосредоточенными параметрами Г-образной схемы замещения |
| 
|
Погрешность любой математической модели можно оценить по норме вектора погрешностей Δ:
, (7)
где ∆ i = 
.
Часто используют евклидову норму и среднеквадратическую погрешность
. (8)
Практическое задание:
Для различных моделей ЛЭП вычислить распределение величины тока и напряжения вдоль ЛЭП при холостом ходе и при передаче мощности меньше и больше натуральной. Выполнить графическое построение графиков тока и напряжения для различных моделей и вычислить погрешности относительно Модели длинной линии с распределенными параметрами. Исходные данные приведены в таблицах 1.1 и 1.2.
Таблица 1.1 – Исходные данные
| Вариант № | Напряжение ЛЭП, кВ | Конструкция фазы | Длина линии, км |
| 8хАС-300/48 | |||
| 5хАС-240/56 | |||
| 3хАС-300/66 | |||
| 2хАС-240/32 | |||
| АС-240/32 | |||
| 8хАС-300/43 | |||
| 5хАС-300/66 | |||
| 3хАС-330/43 | |||
| 2хАС-300/39 | |||
| АС-300/39 | |||
| 5хАС-400/51 | |||
| 3хАС-400/51 | |||
| 2хАС-400/51 | |||
| АС-400/51 | |||
| 4хАС-400/64 | |||
| 3хАС-500/64 | |||
| 2хАС-500/64 | |||
| АС-500/64 | |||
| 4хАС-500/64 | |||
| 8хАС-300/43 | |||
| 5хАС-300/66 | |||
| 3хАС-330/43 | |||
| 2хАС-300/39 | |||
| АС-300/39 | |||
| 4хАС-400/64 | |||
| 3хАС-500/64 | |||
| 2хАС-500/64 | |||
| АС-500/64 | |||
| 8хАС-300/48 | |||
| 5хАС-240/56 |
Таблица 1.2 – Расчетные данные ВЛ 220 кВ и выше со сталеалюминиевыми проводами
| Номинальное сечение, мм2(алюминий/ сталь) | Число проводов в фазе, шт. | r0, Ом/км При 20° С | 1150кВ | 750 кВ | 500 кВ | 330 кВ | 220 кВ | |||||
| x0, Ом/км | b0106 См/км | x0, Ом/км | b0106 См/км | x0, Ом/км | b0106 См/км | x0, Ом/км | b0106 См/км | x0, Ом/км | b0106 См/км | |||
| 240/32 | 0,1180 | - | - | - | - | - | - | - | - | 0,435 | 2,604 | |
| 0,0590 | - | - | - | - | - | - | 0,331 | 3,79 | - | - | ||
| 240/56 | 0,0240 | - | - | 0,308 | 3,76 | - | - | - | - | - | - | |
| 300/39 | 0,0960 | - | - | - | - | - | - | - | - | 0,429 | 2,645 | |
| 0,0480 | - | - | - | - | - | - | 0,328 | 3,41 | - | - | ||
| 300/48 | 0,0123 | 0,266 | 4,433 | - | - | - | - | - | - | - | - | |
| 300/66 | 0,330 | - | - | - | - | 0,31 | 3,97 | - | - | - | - | |
| 0,0200 | – | - | 0,288 | 4,11 | - | - | - | - | - | - | ||
| 330/43 | 0,0290 | - | - | - | - | 0,308 | 3,604 | - | - | - | - | |
| 0,0109 | 0,27 | 4,38 | - | - | - | - | - | - | - | - | ||
| 400/51 | 0,0730 | - | - | - | - | - | - | - | - | 0,42 | 2,701 | |
| 0,0365 | - | - | - | - | - | 0,323 | 3,46 | – | - | |||
| 0,0243 | - | - | - | - | 0,306 | 3,623 | - | - | - | - | ||
| 0,0146 | - | - | 0,286 | 4,13 | - | - | - | - | - | - | ||
| 400/64 | 0,0187 | - | 0,289 | 4,13 | - | - | - | - | - | |||
| 500/64 | 0,0590 | - | - | - | - | - | - | - | - | 0,413 | 2,740 | |
| 0,0295 | - | - | - | - | - | - | 0,32 | 3,497 | - | - | ||
| 0,0197 | - | - | - | 0,304 | 3,645 | - | - | - | - | |||
| 0,0148 | - | - | 0,303 | 3,9 | - | - | - | - | - | - |
Методика решения задачи:
1) Вычислим распределение величины тока и напряжения в режиме холостого хода.
Так как ток I2 =0, то система уравнений длинной линии примет вид
(9)
Определим значения 
и 
.
Изменение напряжения и тока вдоль линии в режиме холостого хода по (10)
(10)
Зададимся значениями х=0..L и построим графики изменения напряжения и тока вдоль линии.
Используем уравнения идеальной линии, модель П-образной схемы замещения и Г-образной схемы замещения с сосредоточенными параметрами и произведем аналогичные расчеты.
Сравним полученные результаты и рассчитаем погрешности каждой модели относительно модели линии с распределёнными параметрами.
2) Вычислим распределение величины тока и напряжения в режиме передачи мощности меньше натуральной, например, Р=0,7Рнат.
Натуральной мощностью ЛЭП Pнат называется активная мощность, передаваемая по ЛЭП, при которой зарядная мощность ЛЭП равна потерям реактивной мощности в ней.
(11)
Вычислим граничные условия: ток I 2, напряжение и ток .
, (12)
где 
.
Изменение напряжения и тока вдоль линии в режиме холостого хода по (2)
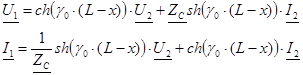
Зададимся значениями х=0..L и построим графики изменения напряжения и тока вдоль линии.
Используем уравнения идеальной линии, модель П-образной схемы замещения и Г-образной схемы замещения с сосредоточенными параметрами и произведем аналогичные расчеты.
Сравним полученные результаты и рассчитаем погрешности каждой модели относительно модели линии с распределёнными параметрами.
3) Вычислим распределение величины тока и напряжения в режиме передачи мощности больше натуральной, например, Р=1,1Рнат.
Вычислим граничные условия: ток I 2, напряжение и ток .
, (12)
где 
.
Изменение напряжения и тока вдоль линии в режиме холостого хода по (2)
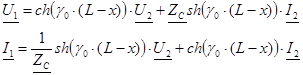
Зададимся значениями х=0..L и построим графики изменения напряжения и тока вдоль линии.
Используем уравнения идеальной линии, модель П-образной схемы замещения и Г-образной схемы замещения с сосредоточенными параметрами и произведем аналогичные расчеты.
Сравним полученные результаты и рассчитаем погрешности каждой модели относительно модели линии с распределёнными параметрами.
Расчётная работа 2.
