Пусть  , т.е.
, т.е. 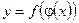 . Тогда
. Тогда
 .
.
Примеры.
Найдём  , пользуясь формулой для производной сложной функции:
, пользуясь формулой для производной сложной функции:
1)  .
.
¨ Здесь 


 .
.
2)  .
.
¨ Здесь 

 .
.
Определение. Логарифмическая производная функции  — это производная от
— это производная от  :
:
 .
.
Определение. Степенно-показательная функция — это функция вида  .
.
Правило нахождения для степенно-показательной функции
1) Логарифмируем  :
:  ;
;
2) Дифференцируем обе части этого равенства:  ;
;
3) Находим из этого соотношения  :
:
 .
.
Примеры нахождения  .
.
1) 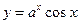 ;
;
¨ 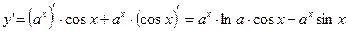 ;
;
2)  ;
;
¨  ;
;
3)  ;
;
¨ а)  ; б)
; б)  ; в)
; в)  ;
;
4)  ;
;
¨ а)  ;
;
б)  ;
;
в)  .
.
Задачи для самостоятельного решения
Найти  :
:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 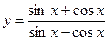 ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12) 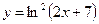 ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15)  ; 16)
; 16)  ; 17)
; 17)  ; 18)
; 18) 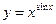 ; 19)
; 19) 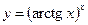 .
.
Занятие №8.
Уравнение касательной и нормали к кривой. Угол между кривыми. Дифференциал функции. Приближённое вычисление значения функции в точке.
Уравнение касательной к кривой  в точке
в точке  имеет вид:
имеет вид:
 . (1)
. (1)
Если 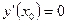 , то
, то  ; если
; если  , то
, то  .
.
Определение. Нормаль к кривой  в точке
в точке  — это прямая, проходящая через точку
— это прямая, проходящая через точку  перпендикулярно касательной.
перпендикулярно касательной.
Уравнение нормали к кривой  в точке
в точке  имеет вид:
имеет вид:
 . (2)
. (2)
Если 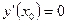 , то
, то  ; если
; если  , то
, то  .
.
 | |||
 | |||







 |





 | |||||
 | |||||
 | |||||



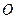


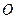

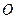

касательная случай случай
нормаль 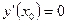

Рис. 1
Определение. Угол 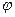 между кривыми
между кривыми  ,
,  в их общей точке — это острый угол между касательными к ним в этой точке. Для вычисления
в их общей точке — это острый угол между касательными к ним в этой точке. Для вычисления 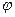 используют формулу:
используют формулу:
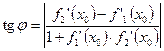 . (3)
. (3)
Определение. Предположим, что приращение функции  в точке
в точке  может быть представлено в виде
может быть представлено в виде
 ,
,
где  — приращение аргумента в точке
— приращение аргумента в точке  , функция
, функция  такова, что
такова, что 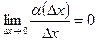 , а
, а  - некоторая константа. Первое слагаемое в этом выражении называют дифференциалом функции
- некоторая константа. Первое слагаемое в этом выражении называют дифференциалом функции  в точке
в точке  и обозначают через
и обозначают через 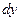 , т.е.:
, т.е.:
 .
.
Приращение  обычно обозначают через
обычно обозначают через 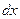 и называют дифференциалом независимой переменной. Таким образом,
и называют дифференциалом независимой переменной. Таким образом,
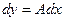 .
.
Можно показать, что  и, следовательно,
и, следовательно,
 .
.
Приближённое вычисление значения функции  в заданной точке.
в заданной точке.
Для этого используется формула:
 . (4)
. (4)
Примеры
1) Написать уравнения касательной и нормали к кривой  в точке
в точке  .
.
¨ Найдём  . Поэтому, согласно формулам (1) и (2):
. Поэтому, согласно формулам (1) и (2):
 — уравнение касательной (или
— уравнение касательной (или  );
);
 — уравнение нормали (или
— уравнение нормали (или  ).
).
2) Найти угол 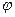 между кривыми
между кривыми  и
и  , а также угол
, а также угол  между касательной к кривой
между касательной к кривой  в точке
в точке  и осью
и осью  .
.
¨ Найдём точку пересечения этих кривых. Для этого решим уравнение  . Оно имеет единственное решение
. Оно имеет единственное решение  . Найдём
. Найдём  ,
, 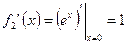 . Далее воспользуемся формулой (3):
. Далее воспользуемся формулой (3):
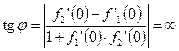 .
.
Поэтому  . Как известно (см. геометрический смысл производной),
. Как известно (см. геометрический смысл производной), 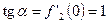 . Поэтому
. Поэтому  .
.
3) Вычислить приближённо: а)  ; б)
; б)  .
.
¨ Во всех случаях подбираем  так, чтобы число
так, чтобы число  было искомым, а
было искомым, а  легко бы определялось. Далее пользуемся формулой (4).
легко бы определялось. Далее пользуемся формулой (4).
а) Возьмём  ,
,  . Тогда
. Тогда  ,
,  ,
, 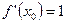

 ;
;
б) Возьмём  ,
,  . Тогда
. Тогда  ,
, 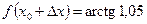 ,
, 

 .
.
Задачи для самостоятельного решения
1) Написать уравнения касательной и нормали к кривой в заданной точке  :
:
а)  ;
;
б) 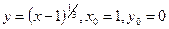 ;
;
в) 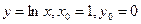 .
.
2) В какой точке касательная к параболе 
а) параллельна прямой  ?
?
б) перпендикулярна прямой  ?
?
3) Найти дифференциал 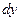 следующих функций:
следующих функций:
а)  ; б)
; б)  ; в)
; в)  .
.
4) Вычислить приближённо:
а)  ; б)
; б)  .
.
Ответы
1) а) 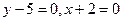 ; б)
; б)  ; в)
; в)  .
.
2) а)  ; б)
; б) 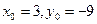 .
.
4) а) 2,25; б) 1.
Занятие №9.
Правило Лопиталя для вычисления пределов. Производная функции, заданной параметрически.
Правило Лопиталя.
1) Пусть надо найти  , где
, где  (или
(или  ), т.е. имеет место неопределённость вида
), т.е. имеет место неопределённость вида 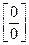 или
или  .Тогда:
.Тогда:
 .
.
(Предполагается, что существуют производные  в окрестности точки
в окрестности точки  , а также существует предел, стоящий справа).
, а также существует предел, стоящий справа).
2) Пусть надо найти  , где
, где  ,
,  , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида  . Тогда следует сделать преобразование:
. Тогда следует сделать преобразование:  , получив неопределённость вида
, получив неопределённость вида 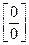 , и воспользоваться указаниями в п.1).
, и воспользоваться указаниями в п.1).
3) Пусть надо найти  , где
, где  ,
,  , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида  . Тогда сделать подходящее преобразование выражения
. Тогда сделать подходящее преобразование выражения  и прийти к случаю 1) или 2).
и прийти к случаю 1) или 2).
4) Пусть надо найти  , где имеется неопределённость вида
, где имеется неопределённость вида  . Пользуясь свойствами логарифма, преобразуем данный предел:
. Пользуясь свойствами логарифма, преобразуем данный предел:

Таким образом, вычисление исходного предела сводится к вычислению предела
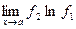 .
.
Замечание. Возможна ситуация, когда существует  , но не существует
, но не существует  . Тогда правило Лопиталя не применимо.
. Тогда правило Лопиталя не применимо.




