Определение. Точка 
называется точкой разрыва I-го рода, если 
конечный. Если в точке разрыва I-го рода 
, то эта точка называется точкой устранимого разрыва, если же 
– то точкой неустранимого разрыва. Точка называется точкой разрыва II-го рода, если хотя бы один из односторонних пределов 
не существует или равен бесконечности.
Геометрическая иллюстрация этих определений:
Примеры:
1) Как выбрать число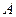 
, чтобы 
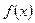была непрерывна в точке 
?
▲ Функция 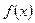непрерывна в точке 
.
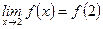Найдем 
. Поэтому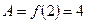 
.
2) Как выбрать число 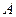, чтобы 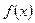была непрерывна в точке 
?
▲ Имеем: 
.
Функция 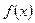непрерывна в точке 
.
Отсюда получаем: 
, т.е. 
.
3) Сформулируем общий принцип построения и решения задач типа 1) и 2). Функция 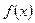задается формулой:
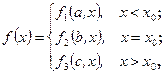
где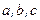 
– некоторые параметры, 
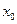– фиксированная точка. Требуется подобрать значения параметров 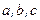так, чтобы 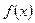была непрерывна в точке 
.
▲ Находим односторонние пределы функции в точке :
, 
.
Для непрерывности 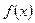в точке необходимо и достаточно, чтобы 
, т.е.
(*)
Как правило, функции 
непрерывны, так что вычисление соответствующих пределов не составляет труда. Из получаемых соотношений (*) находим .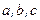
4) Как доопределить функцию 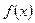в точке 
, чтобы 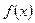стала непрерывной в точке ?
а) 
; б) 
; в) 
▲ Для непрерывности 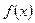в точке необходимо и достаточно, чтобы 
. Поэтому:
а) 
(произведение бесконечно малой функции 
на ограниченную функцию 
есть бесконечно малая функция);
б)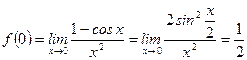 
;
в) 
.
Замечание. Для построения задач типа 4) можно взять любую функцию 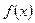из раздела "Вычисление пределов", для которой пределу 
соответствует неопределенность вида 
.
5) Исследовать функцию на непрерывность:
а) 
.
▲ Точка 
– точка разрыва, т.к. функция в ней не определена; это – точка разрыва I-го рода; устранимого разрыва, т.к.
б) 
.
▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к. 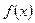не определена в этой точке. Это точка разрыва I-го рода, причем разрыв неустранимый, т.к.
, 
.
в) 
.
▲ Функция непрерывна во всех точках, кроме точек вида , 
. В этих точках – разрыв, т.к. 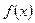не определена в них. В точке разрыв I-го рода, причем устранимый, т.к.
.
В точках вида – разрыв II-го рода, т.к.
.
г) 
.
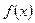▲ Функция непрерывна во всех точках, кроме точки . В этой точке разрыв, т.к. не определена в этой точке. В точке – разрыв I-го рода, причем неустранимый, т.к.
, 
.
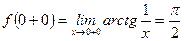д) 
.
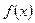▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к. не определена в этой точке. В точке – разрыв II-го рода, т.к.
,
.
е) 
.
▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к. 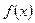не определена в этой точке. В этой точке – разрыв I-го рода, причем неустранимый, т.к.
,
.
