Фирма рассматривает инвестиционный проект по производству продукта "А". В процессе предварительного анализа экспертами были выявлены три ключевых параметра проекта и определены возможные границы их изменений (таблица 1.1). Прочие параметры проекта считаются постоянными величинами (таблица 1.2).
Таблица 1.1 - Ключевые параметры проекта по производству продукта "А"
| Показатель | Наихудший | Наилучший | Вероятный |
| Объем выпуска - Q | |||
| Цена за штуку - P | |||
| Переменные затраты - V |
Таблица 1.2 - Неизменяемые параметры проекта по производству продукта"А"
| Показатели | Наиболее вероятное значение |
| Постоянные затраты - F | |
| Амортизация - A | |
| Налог на прибыль - T | 60% |
| Норма дисконта - r | 10% |
| Срок проекта - n | |
| Начальные инвестиции - I0 |
Предположим, что используемым критерием оценки риска является чистая современная стоимость проекта NPV:
n
NPV=S (NCFt / (1 + r)t - I0)
t=1
где:
NCFt - величина чистого потока платежей в периоде t.
По условиям примера, значения нормы дисконта r и первоначального объема инвестиций I0 известны и считаются постоянными в течение срока реализации проекта (таблица 1.2).
В целях упрощения будем полагать, что величина потока платежей NCF для любого периода t одинакова и может быть определена из следующего соотношения:
NCFt = Qt(Pt – Vt) – F – A)(1 – T) + A
Следующими этапом проведения анализа является выбор законов распределения вероятностей ключевых переменных.
По условиям примера ключевыми варьируемыми параметрами являются: переменные расходы V, объем выпуска Q и цена P. Диапазоны возможных изменений варьируемых показателей приведены в таблице 3.1. При этом будем исходить из предположения, что все ключевые переменные имеют равномерное распределение вероятностей.
Проведение имитационных экспериментов в среде ППП EXCEL можно осуществить двумя способами - с помощью встроенных функций и путем использования инструмента "Генератор случайных чисел" дополнения "Анализ данных" (Analysis ToolPack). Эти инструменты подключаются через пункты меню (Главная кнопка – Параметры - Надстройки – Пакет анализа – Перейти - ОК).
Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9]. В нашем примере необходимо установить режим ручных вычислений (Главная кнопка – Параметры – Формулы – Параметры вычислений – Вручную).
В расчетах будут использоваться функции, описание которых приведено ниже.
Функция СЛУЧМЕЖДУ(нижн_граница; верхн_граница)
Как следует из названия этой функции, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (т.е. вещественное или целое) зависит от типа заданных аргументов.
В качестве примера, сгенерируем случайное значение для переменной Q (объем выпуска продукта).
Введите в любую ячейку ЭТ формулу:
=СЛУЧМЕЖДУ(150; 300) (Результат: 210).
Если задать аналогичные формулы для переменных P и V, а также формулу для вычисления NPV и скопировать их требуемое число раз, можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов. После чего нетрудно рассчитатьсоответствующие параметры распределения и провести вероятностный анализ.
Продемонстрируем изложенный подход на решении приведенного выше примера. Перед тем, как приступить к разработке шаблона, целесообразно установить в ЭТ режим ручных вычислений.
Приступаем к разработке шаблона. С целью упрощения и повышения наглядности анализа выделим для его проведения в рабочей книге ППП EXCEL два листа.
Первый лист - "Имитация", предназначен для построения генеральной совокупности (рис. 1.1). Его необходимо создать в точном соответствии с рисунком. Далее необходимо задать имена соответствующим диапазонам ячеек. Учтите, что количество имитационных экспериментов 500, соответственно диапазоны ячеек включают строки с десятой по пятьсот десятую (выделяете диапазоны и затем используйте команду ФОРМУЛЫ – ПРИСВОИТЬ ИМЯ). Имена приведены в таблице 1.3.
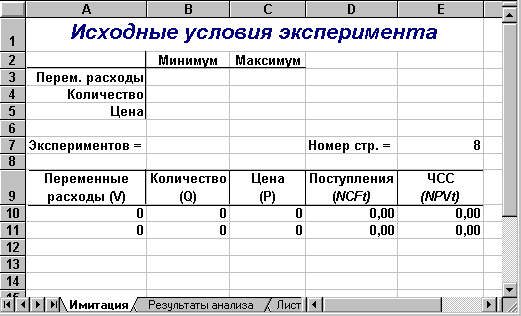
Рис. 1.1 - Лист "Имитация"
Таблица 1.3 - Имена ячеек листа "Имитация"
| Адрес ячейки | Имя | Комментарии |
| Блок A10:A510 | Перем_расх | Переменные расходы |
| Блок B10:B510 | Количество | Объем выпуска |
| Блок C10:C510 | Цена | Цена изделия |
| Блок D10:D510 | Поступления | Поступления от проекта NCFt |
| Блок E10:E510 | ЧСС | Чистая современная стоимость NPV |
После того, как создан первый лист «Имитация» и соответствующим диапазонам ячеек назначены имена, необходимо приступить к созданию второго листа «Результаты анализа». Шаблон этого листа приведен на рис. 1.2. Имена ячеек листа приведены в таблице 1.4.
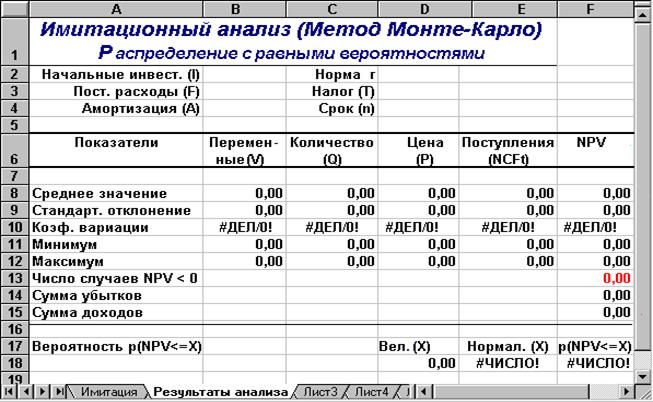
Рис. 1.2 – Лист «Результаты анализа»
Таблица 1.4 - Имена ячеек листа "Результаты анализа"
| Адрес ячейки | Имя | Комментарии |
| B2 | Нач_инвест | Начальные инвестиции |
| B3 | Пост_расх | Постоянные расходы |
| B4 | Аморт | Амортизация |
| D2 | Норма | Норма дисконта |
| D3 | Налог | Ставка налога на прибыль |
| D4 | Срок | Срок реализации проекта |
После того, как два листа созданы и определены имена ячеек и диапазонов, необходимо приступить к вводу соответствующих формул. Эти формулы представлены в таблицах 1.5 и 1.6. Обратите внимание на то, что при указании нижней и верхней границы изменений используется абсолютная адресация ячеек.
Таблица 1.5 - Формулы листа "Имитация"
| Ячейка | Формула |
| A10 | =СЛУЧМЕЖДУ($B$3;$C$3) |
| B10 | =СЛУЧМЕЖДУ($B$4;$C$4) |
| C10 | =СЛУЧМЕЖДУ($B$5;$C$5) |
| D10 | =(B10*(C10-A10)-Пост_расх-Аморт)*(1-Налог)+Аморт |
| E10 | =ПС(Норма;Срок;-D10)-Нач_инвест |
Примечание: Формулы в таблице 5 необходимо скопировать в соответствующие диапазоны до номера строки – 510.
Таблица 1.6 - Формулы листа "Результаты анализа"
| Ячейка | Формула |
| B8 | =СРЗНАЧ(Перем_расх) |
| B9 | =СТАНДОТКЛОНП(Перем_расх) |
| B10 | =B9/B8 |
| B11 | =МИН(Перем_расх) |
| B12 | =МАКС(Перем_расх) |
| C8 | =СРЗНАЧ(Количество) |
| C9 | =СТАНДОТКЛОНП(Количество) |
| C10 | =C9/C8 |
| C11 | =МИН(Количество) |
| C12 | =МАКС(Количество) |
| D8 | =СРЗНАЧ(Цена) |
| D9 | =СТАНДОТКЛОНП(Цена) |
| D10 | =D9/D8 |
| D11 | =МИН(Цена) |
| D12 | =МАКС(Цена) |
| E8 | =СРЗНАЧ(Поступления) |
| E9 | =СТАНДОТКЛОНП(Поступления) |
| E10 | =E9/E8 |
| E11 | =МИН(Поступления) |
| E12 | =МАКС(Поступления) |
| F8 | =СРЗНАЧ(ЧСС) |
| F9 | =СТАНДОТКЛОНП(ЧСС) |
| F10 | =F9/F8 |
| F11 | =МИН(ЧСС) |
| F12 | =МАКС(ЧСС) |
| F13 | =СЧЁТЕСЛИ(ЧСС;"<0") |
| F14 | =СУММЕСЛИ(ЧСС;"<0") |
| F15 | =СУММЕСЛИ(ЧСС;">0") |
| Е18 | =НОРМАЛИЗАЦИЯ(D18;$F$8;$F$9) |
| F18 | =НОРМСТРАСП(E18) |
Лист "Результаты анализа" кроме значений постоянных переменных содержит также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Приведем описание этих функций.
Функции МИН() и МАКС() вычисляют минимальное и максимальное значение для массива данных из блока ячеек, указанного в качестве их аргумента.Имена и диапазоны этих блоков приведены в таблице 3.6.
Функция СЧЕТЕСЛИ() осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат:
=СЧЕТЕСЛИ(блок; "условие").
В данном случае, заданная в ячейке F13, эта функция осуществляет подсчет количества отрицательных значений NPV, содержащихся в блоке ячеек ЧСС.
Механизм действия функции СУММЕСЛИ() аналогичен функции СЧЕТЕСЛИ(). Отличие заключается лишь в том,что эта функция суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат:
=СУММЕСЛИ(блок; "условие").
Две последние формулы (ячейки Е18и F18) предназначены для проведения вероятностного анализа распределения NPV.
Функция НОРМАЛИЗАЦИЯ(x; среднее; станд_откл)
Эта функция возвращает нормализованное значение Z величины x, на основании которого затем вычисляется искомая вероятность p(E £ x). Она реализует вышеприведенную формулу. Функция требует задания трех аргументов:
х - нормализуемое значение;
среднее - математическое ожидание случайной величины Е;
станд_откл - стандартное отклонение.
Полученное значение Z является аргументом для следующей функции - НОРМСТРАСП().
Функция НОРМСТРАСП(Z)
Эта функция возвращает стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна х. Она имеет всего один аргумент - Z, вычисляемый функцией НОРМАЛИЗАЦИЯ().
Нетрудно заметить,что эти функции следует использовать вместе. При этом наиболее эффективным и компактным способом их задания является указаниефункции НОРМАЛИЗАЦИЯ() в качестве аргумента функции - НОРМСТРАСП(), т.е.:
=НОРМСТРАСП(НОРМАЛИЗАЦИЯ(x; среднее; станд_откл)).
С целью повышения наглядности, в проектируемом шаблоне функции заданы раздельно (ячейки Е18 и F18).
Сформируйте данный шаблон и сохраните его на магнитном диске под именем SIMUL_1. Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги.
1. Ввести значения постоянных переменных (табл. 1.2) в ячейки В2:В4 и D2:D4 листа "Результаты анализа".
2. Ввести значения диапазонов изменений ключевых переменных (табл. 1.1) в ячейки В3:С5 листа "Имитация".
3. Нажатием клавиши F9 провести расчет.
4. Перейти к листу "Результаты анализа" и проанализировать полученные результаты.
Результатом выполнения этих действий будет заполнение блока А10:Е510случайными значениями ключевых переменных V, Q, P и результатами вычислений величин NCF и NPV. Фрагмент результатов имитации приведен на рис. 1.3. Соответствующие проведенному эксперименту результаты анализа приведены на рисунке 1.4.
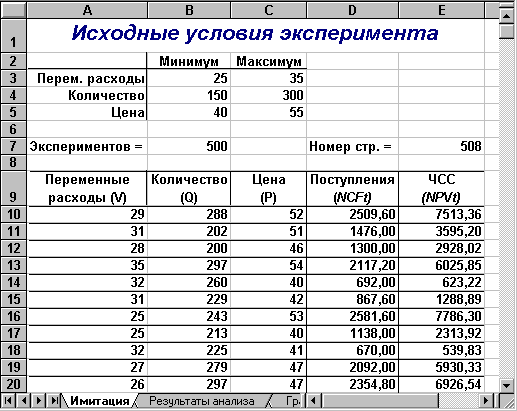
Рис. 1.3- Результаты имитации
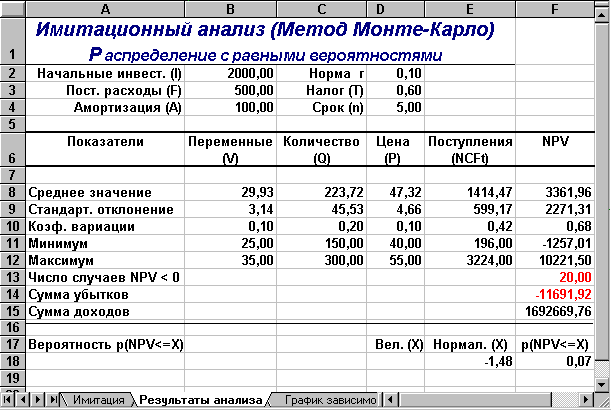
Рис. 1.4 - Результаты анализа
Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.
В данном случае они наглядно демонстрируют несоизмеримость суммы возможных убытков по отношению к общей сумме доходов (-11691,92 и 1692669,76 соответственно).
На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Ограничимся визуальным (графическим) исследованием. На рисунке 1.5 приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 75 имитаций.
Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу об их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (рисунок 1.6).
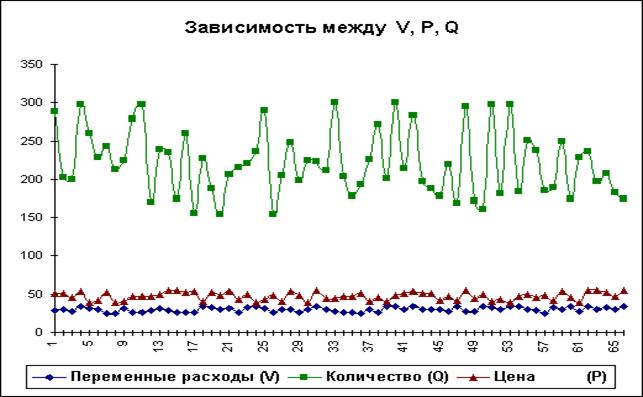
Рис. 1.5 Распределение значений параметров V, P и Q
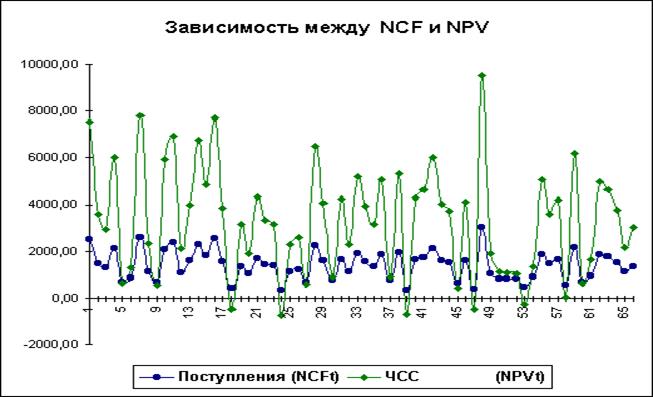
Рис. 1.6 - Зависимость между NCF и NPV
Задание к лабораторной работе № 1
Дана рецептура пищевого продукта с соответствующими рецептурными ингредиентами (РИ), также известна энергетическая ценность каждого ингредиента (ккал) и стоимость в рублях/кг. Необходимо провести имитационный эксперимент с использованием функции СЛУЧМЕЖДУ, определить статистические показатели по каждому из РИ, а также статистические показатели по суммарной энергетической ценности и стоимости продукта (или других показателей в зависимости от варианта задания). Результаты оформить в виде файла MS Excel – рисунок 1. Рассчитать количество случаев, при которых стоимость и энергетическая ценность оказались меньше среднего значения. Определить вероятность того, что стоимость и энергетическая ценность будут меньше среднего значения. Начертить графики изменения каждого показателя по первым 50 значениям.
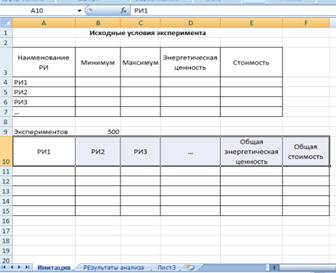
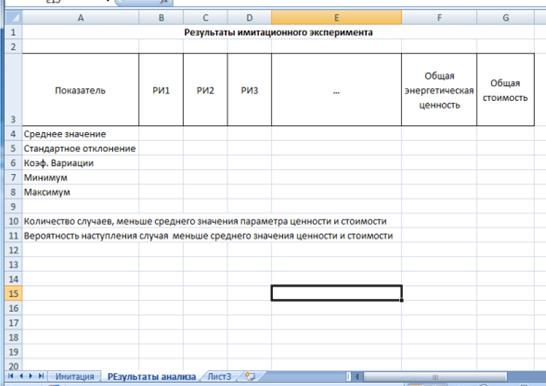
Рисунок 1 – Оформление расчетов в табличном процессоре
Варианты для расчета
Вариант 1. Рецептура глазированных желейных конфет вида 1.
| Наименование РИ | Минимум | Максимум | Энергетическая ценность ккал/ед. | Стоимость руб./ед. |
| Сахар-песок | 26,4 | |||
| Патока крахмальная | ||||
| Пектин цитрусовый | ||||
| Цитрат натрия | 1,5 | |||
| Лимонная кислота | 0,3 | |||
| Шоколадная глазурь |
Вариант 2. Рецептура глазированных желейных конфет вида 2.
| Наименование РИ | Минимум | Максимум | Энергетическая ценность ккал/ед. | Стоимость руб./ед. |
| Сахар-песок | 26,4 | |||
| Фруктоза | ||||
| Патока крахмальная | ||||
| Пектин цитрусовый | ||||
| Цитрат натрия | 1,5 | |||
| Лимонная кислота | 0,3 | |||
| Шоколадная глазурь |
Вариант 3. Рецептура медовой пасты
| Наименование РИ | Минимум, г | Максимум, г | Содержание кальция (мг/100 г) | Содержание витамина С (мг/100 г) |
| Ядро арахиса | 5,3 | |||
| Изюм | ||||
| Семена тыквы | ||||
| Чернослив | ||||
| Курага | ||||
| Мед пчелиный |
Вариант 4. Рецептура плавленого сыра «Кубаночка»
| Наименование РИ | Минимум, кг | Максимум, кг | Содержание белков г/100 г | Стоимость руб./кг |
| Сыр свежий несоленый | 26,8 | |||
| Сыр нежирный | 25,3 | |||
| Молоко коровье сухое обезжиренное | 37,9 | |||
| Масло крестьянское | 0,96 | |||
| Смесь триполифосфата натрия и натрия пирофосфорнокислого пищевого | 21,5 | |||
| Сахар песок | ||||
| Вода питьевая |
Лабораторная работа № 2






