3.1. Используемые операторы. Для изучения начальной задачи (2.1), (2.5) потребуется оператор
(1)
действующий в пространстве 
). Соответствующий оператор для задачи (2.3), (2.6) действует в том же пространстве и имеет вид
(2)
При условии непрерывности оператора f по совокупности переменных при каждом фиксированном 
операторы 
и 
вполне непрерывны в пространстве ) и их неподвижные точки являются решениями соответствующих начальных задач.
В задаче о Т- периодических решениях системы (2.1) применяется оператор
(3)
действующий в пространстве 
). При каждом фиксированном с оператор (3) также вполне непрерывен и его неподвижные точки определяют, после Т- периодического продолжения на всю ось, Т- периодические решения системы (2.1) (см. [7]).
3.2. Индекс интегральной воронки. Рассмотрим уравнение
(4)
где оператор 
и непрерывен по совокупности переменных.
3.3. Предложение. Пусть интегральная воронка уравнения (4) с начальным условием
(5)
ограничена на отрезке [0, d]. Тогда индекс множества неподвижных точек оператора F, действующего в пространстве 
) и задаваемого формулой
(6)
равен 1.
Доказательство. Обозначим через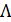 
множество решений задачи (4), (5) на отрезке [0, d]. Множество неподвижных точек оператора (6) в пространстве ) совпадает с 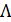. Пусть U – произвольное ограниченное открытое множество пространства ), содержащее 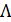. Множество 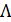замкнуто. Поэтому Fне имеет неподвижных точек на 
. Кроме того, оператор 
, где L –замкнутое, выпуклое подмножество пространства ), определяемое равенством
По теореме о сужении 1.3
Продолжим функции из множества 
на отрезок 
константой по непрерывности. Рассмотрим оператор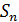 
, определяемый на множестве равенством
Возьмем произвольную функцию 
. Положим
.
Поскольку операторы 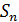сильно сходятся к тождественному оператору, то операторы 
вполне непрерывны по совокупности переменных, 
. Покажем, что операторы 
и 
при достаточно больших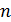 
линейно гомотопны на 
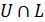. Допустим противное. Тогда существуют последовательности 
такие, что 
и
Из последнего равенства следует
и, следовательно относительно компактна. Без ограничения общности можно считать, что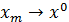 
, а 
. Перепишем равенство более подробно
В силу непрерывности оператора и сильной сходимости операторов 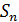к тождественному оператору в равенстве можно перейти к пределу при 
Тогда получим 
и 
В чем противоречие. Итак, в силу свойства 
п.1.2 и равенства
при достаточно больших .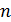
Покажем, что отображение 
и задаваемое формулой
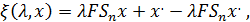
Является гомотопией, соединяющей операторы 
и 
Действительно, полная непрерывность оператора 
вытекает из полной непрерывности оператора . Кроме того при любом 
уравнение
Имеет единственное решение 
. При 
последнее очевидно, а при 
, если уравнение имеет решение 
, то 
, следовательно, 
при 
Поэтому 
при Тогда при 
.Продолжая далее, придем к равенству при 
Для завершения доказательства осталось воспользоваться свойствами и 
п. 1.2. Тогда
Учитывая равенство , находим
3.4. Доказательство теоремы 2.1. Обозначим через 
множество решений задачи 
на отрезке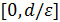 
. Пусть 
- 
-раздутие множества в пространстве 
Покажем, что при достаточно малых 
операторы и , определенные формулами 
, линейно гомотопны на множестве 
в пространстве Допустим противное, тогда существуют последовательности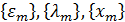 
такие, что
И 
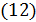
Делая в 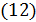замену переменных 
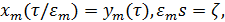получим, что для последовательности 
пространства 
справедливо 
и
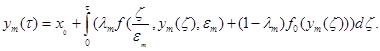
(13)
Заметим, что последовательность { 
} относительно компактна как сумма постоянной и двух ограниченных равностепенно непрерывных последовательностей. Без ограничения общности будем считать, что 
, т.е.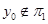 
. В силу Т-периодичности по t оператора f в равенстве (13) можно перейти к пределу при 
. Тогда
т.е. 
- решение при ε=1 задачи (2.3), (2.6) на отрезке [0,d], не принадлежащее 
, в чем противоречие. Итак, операторы 
и 
гомотопны. Так как в силу предложения 3.3
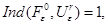
то в силу свойства 
индекса (см. п. 1.2)
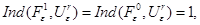
и по свойству 4 индекса оператор имеет в 
неподвижную точку, а задача (2.1), (2.5) – решение на отрезке [0, d/ε].
Для доказательства неравенства (2.7) покажем, что при достаточно малых ε все решения задачи (2.1), (2.5) определены на [0, d/ε] и лежат в 
Допустим противное, тогда существуют последовательности 
такие, что 
- решение задачи (2.1), (2.5), определенное на отрезке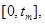 
причем 
при 
и 
Заметим, что в силу T- периодичности по t оператора f и его непрерывности по совокупности переменных существует константа M>0 такая, что
,
(14)
где 
- r- раздутие множества 
, определенного в п.2.3. Поэтому 
Без ограничения общности можно считать, что последовательность точек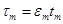 
сходится к некоторому 
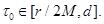Функции 
на отрезках 
удовлетворяют уравнению
(15)
Делая в (15) замену переменных 
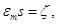получим, что для последовательности функций , определенных на отрезках 
, справедливо 
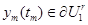и
(16)
Будем считать, что функции определены на отрезке 
, продолжив, если это необходимо, их с отрезка на отрезок по непрерывности константой. За таким продолжением сохраним прежнее обозначение. Заметим, что последовательность 
относительно компактна в пространстве 
Без ограничения общности будем считать, что 
Тогда 
В силу T-периодичности по t оператора f в равенстве (16) можно перейти к пределу при . Тогда
т.е. - решение при ε=1 задачи (2.3), (2.6) на отрезке Все решения задачи (2.3), (2.6) при ε=1 определены на отрезке 
Поэтому решение может быть продолжено на отрезок Но так продолженное решение не принадлежит , так как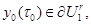 
в чем противоречие.∎
3.5. Доказательство замечания 2.3. При доказательстве теоремы 2.1 все рассуждения проводились в случае, когда аргументы оператора f лежат в множестве 
(напомним - r- раздутие множества , определенного в п.2.3). Поэтому и непрерывность оператора f достаточно потребовать на множестве (2.9).∎
3.6. Доказательство замечания 2.4. Периодичность оператора f была использована при доказательстве теоремы 2.1 при предельном переходе в равенствах (13) и (16), а так же при получении оценки (14). В условиях замечания 2.4 предельный переход обеспечивается леммой М.А. Красносельского - С.Г. Крейна (см. [7]), а оценка (14) вытекает из ограниченности оператора f на множестве (2.9).∎
3.7. Доказательство теоремы 2.5. В пространстве 
рассмотрим ограниченное открытое множество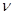 
, определяемое формулой
(17)
Покажем, что при достаточно малых ε на множестве 
оператор 
, заданный формулой (3), линейно гомотопен оператору
Допустим противное. Тогда существуют последовательности 
и 
такие, что
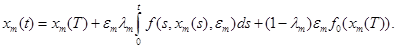
(18)
Заметим, что непрерывно дифференцируемы и
Так как 
, то 
равномерно ограничены, поэтому в силу непрерывности оператора f имеем
(19)
Где С – некоторая константа. Следовательно, последовательность 
вполне ограничена. Будем считать, что 
,тогда в силу оценки (19) функция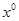 
- константа, т.е. 
Полагая в равенстве (18) t=T и деля на ε, получим
Переходя к пределу при 
найдем
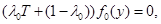
т.е. – решение уравнения
,
(20)
лежащее на границе множества 
, в чем противоречие. В силу свойства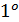 
индекса (см. п. 1.2)
Оператор 
отображает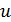 
в подпространство функций констант изоморфное 
. Поэтому, применяя теорему о суждении 1.3, будем иметь
?
Поскольку уравнение (20) не имеет решений, принадлежащий 
, оператор 
гомотопен оператору 
. Гомотопия задаётся формулой
Итак,
(21)
Воспользовавшись свойством 
индекса п. 1.2, получим, что при достаточно малых ε система (2.1.1) имеет -периодическое решение 
, лежащее в ,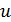
т.е. 
при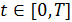 
.
Пусть теперь 
, и последовательность при (
) 
-периодических решений 
Системы (2.1), лежащих в 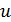, равномерно сходится к некоторой предельной функции 
. Тогда для функции справедлива оценка (19). Поэтому 
- функция константа. Пусть 
. Так как - -периодическое решение системы (2.1), то для них выполнено равенство
Переходя в последнем равенстве к пределу при 
, получим, что является решением уравнения (20), т.е. состоянием равновесия. 
Следствие 2.6 вытекает из теоремы 2.5, если в качестве множества взять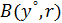 
.
Следствие 2.7 следует из теоремы 1.4.
Литература
1. Ахмеров Р.Р., Каменский М.И. Ко второй теореме Н.Н.Боголюбова в принципе усреднения для функционально- дифференциальных уравнений нейтрального типа // Дифференц. Уравнения. – 1974. – 13. – с. 537-540.
2. Ахмеров Р.Р., Каменский М.И., Родкина А.Е., Потапов А.С., Садовский Б.Н. Меры некомпактности и уплотняющие опертаоры. – Новосибирск: Наука, 1986.
3. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. –М.:Наука, 1974.
4. Гурова Н.Н. Одно утверждение типа принципа родственности и вторая теорема Н.Н. Боголюбова в принципе усреднения параболических уравнений // Качественные методы исследования операторных уравнений. – Ярославль, 1982. –с. 47-58.
5. Каменский М.И. О принципе усреднения для квазилинейных параболических уравнений с запаздыванием. // Доклады Академии наук. – 1994. – 337,N3. –с. 304-306.
6. Климов В.С. К задаче о периодических решениях операторных дифференциальных включений // Известия АН СССР. Математическая серия. 1989. -53, N2. – c.309-327/
7. Красносельский М.А., Забрейко П.П. Геометрические методы нелинейного анализа. –М.: Наука, 1975.
8. Красносельский М.А., Крейн С.Г. О принципе усреднения в нелинейной механике // Успехи мат. наук. – 1955. -10, N 3(65). – с. 147-152.
9. Потапова Л.В. Принцип усреднения и периодические решения параболического уравнения с запаздывающим аргументом // Укр. мат. ж. -1985. -37, N2. –c.198-205.
10. Самоленко А.М. Численно-аналитический метод исследования периодических систем обыкновенных дифференциальных уравнений. I, II // Украинский математический журнал. 1965. -17, -4. –с. 82-93; 1966. -18. -2. –с. 50-59.
11. Стрыгин В.В. Одна теорема о существовании периодических решений систем дифференциальных уравнений с запаздывающим аргументом // Мат. заметки. – 1970. – 8. N2. –c. 229-233.
Содержание
§1. Теория топологического индекса вполне непрерывных операторов………………….2
§2. Классические первая и вторая теорема Н.Н. Боголюбова- Н.М. Крылова с формулировкой условий в терминах топологического индекса……………………………....3
§3. Доказательства результатов из параграфа 2………………………………………………………….6
Составитель Каменский Михаил Игоревич
Редактор Кузнецова З.Е.
Тираж 100 экз. Множительная техника математического факультета ВГУ
