Теория топологического индекса вполне непрерывных операторов.
Через 
обозначается открытое ограниченное множество банаховапространства 
. Через 
– егограница и замыкание соответственно. Всюду ниже 
– вполне непрерывный оператор.
1.1. Допустимые гомотопии. Два вполне непрерывных оператора
называются гомотопными, если существует вполне непрерывный по совокупности переменных оператор 
, такой что 
, 
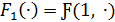и 
не имеет неподвижных точек на 
при 
.
Гомотопия называется линейной, если она задается формулой:
.
1.2. Индекс множества неподвижных точек вполне непрерывного оператора. Если вполне непрерывный оператор 
не имеет неподвижных точек на границе , то определена целочисленная характеристика, называемая индексом множества неподвижных точек оператора и обозначаемая 
, со следующими свойствами:
1 
. Индексы гомотопных вполне непрерывных операторов совпадают.
2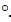 
Пусть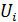 
, 
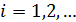попарно непересекающиеся открытые подмножества 
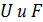не имеют неподвижных точек в 
Тогда величины 
определены для всех i, только дляконечного числа из них отличны он нуля и 
3 . Если 
4 Если 
то оператор имеет по крайней мере одну неподвижную точку в 
Если 
изолированная неподвижная точка оператора 
т.е. в некотором шаре 
у оператора нет других неподвижных точек, то индексом 
называют величину 
, при 
.
Индексом точки обозначают 
.
1.3. Теорема о сужении. Пусть L замкнутое выпуклое подмножество пространства E и
Не имеет неподвижный точек на 
. Тогда
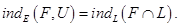
1.4. Теорема о вычислении индекса по линейной части. Пусть вполне непрерывный оператор F, действующий в банаховом пространстве E, определен в некоторой окрестности своей неподвижной точки 
и дифференцируем по Фреше в точке . Пусть 1 не является собственным значением линейного оператора 
Тогда является изолированной неподвижной точкой оператора F и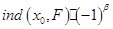 
, где β-сумма кратностей вещественных больших единицы собственных значений оператора
Классические первая и вторая теоремы Н.И. Боголюбова – Н.М. Крылова с формулировкой условий в терминах топологического индекса.
Опишем обобщения классических теорем Н.И. Боголюбова – Н.М. Крылова (см. (3)), получающиеся при применении теории топологического индекса.
Рассмотрим систему обыкновенных дифференциальных уравнений
,
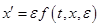(1)
где 
-положительный параметр. Предположим, что
(2)
Принцип усреднения заключается в оценке близости решений системы (1) к решениям обычно более простой автономной системы
(3)
где
(4)
Рассмотрим задачу Коши. Пусть решения 
и 
систем (1) и (3) удовлетворяют одинаковому начальному условию
(5)
(6)
Перед формулировкой теоремы напомним, интегральной воронкой решений системы дифференциальных уравнений называют множество ее решений, удовлетворяющих одному и тому же начальному условию.
2.1. Теорема. Пусть оператор 
непрерывен по совокупности переменных и интегральная воронка системы (3) с начальным условием (6) при 
ограничена на отрезке 
.
Тогда каждому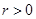 
соответствует такое 
, что при 
на отрезке 
интегральная воронка ограничена и для любого решения системы (1) с начальным условием (5) существует решение системы (3) с начальным условием (6) такое, что
(7)
Когда интегральная воронка задачи (3),(6) при состоит из одного решения, то теорема 2.1 превращается в следующее утверждение.
2.2 Следствие. Пусть оператор непрерывен по совокупности переменных и система (3) с начальным условием (6) при имеет единственное решение на отрезке .
Тогда каждому 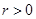соответствует такое , что при верна оценка
(8)
2.3. Замечание. В теореме 2.1.1 и следствии 2.1.2 требование непрерывности оператора можно заменить менее ограничительным требованием непрерывности лишь на
(9)
Где 
- некоторая окрестность множества
.
2.4. Замечание. Аналогичные теоремы 2.1 и следствие 2.2 утверждения можно доказать и когда правая часть системы (1) не обладает свойством T-периодичности по времени (т.е., когда неверны тождества (2)). В этом случае вместо оператора 
, определяемого равенством (4), используется оператор
(10)
При этом предполагается, что среднее (10) существует, и предел (10), равномерен относительно 
из каждого фиксированного шара, а - равномерно непрерывен и ограничен на множестве (9).
Перейдем к задаче о T- периодических решениях системы (1) и к обсуждению возможностей приближенного построения этих решений при помощи системы (3). Предположим, что для некоторого ограниченного открытого множества 
векторное поле - 
не имеет нулевых точек на границе 
. Тогда определен 
.
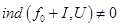2.5. Теорема. Пусть .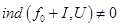
Тогда существует такое , что при система (1) имеет по крайней мере одно T – периодическое решение 
, для которого справедливо соотношение 
. Причем для любой последовательности 
, сходящейся к нулю, последовательность решений 
вполне ограничена и ее предельными точками могут быть только состояния равновесия системы (3), лежащие в .
Важным случаем является ситуация, когда состояние равновесия 
системы (3) изолировано. Тогда определен индекс множества
нулевых точек векторного поля - 
в пространстве 
на шарах малых радиусов с центром в 
., т.е. 
.
2.6. Следствие. Пусть . – изолированный нуль векторного поля 
, причем выполнено условие
(11)
Тогда каждому r>0 соответствует такое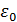 
>0, что при 
система (1) имеет по крайней мере одно Т- периодическое решение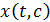 
, для которого справедлива оценка
(12)
Через А обозначается следующая матрица
(13)
2.7. Следствие. Пусть . – нуль векторного поля , причём выполнено условие
(14)
Тогда каждому r>0 соответствует такое 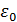>0, что при система (1) имеет по крайней мере одно Т-периодическое решение 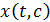, для которого справедлива оценка (12).
