Статистический анализ случайных ошибок

При проведении серии измерений некоторой физической величины (например, длины, с помощью линейки или силы тока с помощью амперметра) из-за случайных ошибок отдельные значения x ₁, x ₂, и т. д. неодинаковы.

Абсолютная погрешность определяет границы интервала, внутри которого с некоторой вероятностью заключено «истинное значение» искомой величины, и она равна взятой по модулю разности между «истинным значением» измеряемой величины и его приближенным значением x_i.

Но так как «истинное значение» измеряемой величины остается неизвестным, то в качестве наилучшего значения искомой величины принимают среднее арифметическое:

(1.1)

где x _i – i -е измеренное значение, a n - общее число измерений. Абсолютная погрешность отдельного i-го измерения запишется тогда так

или , ед. измерения.

Относительной погрешностью e_x называется отношение абсолютной погрешности к значению x_ист, т.е.

.

Относительная погрешность является безразмерной величиной (её выражают или в долях единицы, или в процентах).

Для оценки величины случайной ошибки (погрешности) измерения обычно используют величину - дисперсию измерения (стандартное отклонение)

, (1.2)

где n – общее число измерений.

Если стандартное отклонение мало, то разброс измеренных значений относительно среднего значения является малым, следовательно, точность измерения высокая. Заметим, что стандартное отклонение является всегда положительным и имеет ту же размерность, что и измеренные значения.

Чем больше повторений, тем выше точность измерений. Причина улучшения заключается в том, что положительные и отрицательные ошибки частично компенсируются при усреднении результатов нескольких измерений.

Поэтому в качестве меры погрешности результатов измерений величины x (или неопределенности среднего значения ) принимают стандартное отклонение от среднего S_n,которое часто называют средним квадратичным отклонением или стандартной погрешностью и определяют как

. (1.3)

Абсолютная погрешность Dx измеряемой величины x при относительно малом количестве измерений (например, 10 - 100) определяется формулой:

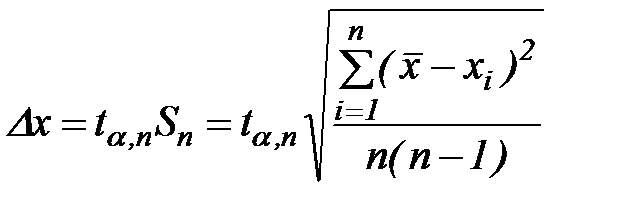, (1.4)

где t _{a, n} – коэффициент (коэффициент Стьюдента), - полная абсолютная погрешность или доверительный интервал, внутри которого находится истинное значение величины . Коэффициент Стьюдента зависит от числа измерений n и от величины доверительной вероятности a (табл. 1). В соответствии с действующими государственными стандартами рекомендуется при оценке погрешностей пользоваться доверительной вероятностью a = 0,95.

Коэффициенты Стьюдента Таблица 1.1.

Таким образом, окончательный результат измерений запишется в виде:

, ед. измерений, (1.5)

где D x определяется из выражения (1.4). Запись (1.5) означает, что истинное значение величины x с вероятностью a находится в интервале (доверительном интервале) значений от до .