Протекания процесса и условий равновесия в системе

при V= Const и Т= Const

 

Из объединённого уравнения первого и второго законов термодинамики следует, что

 

δA ≤ TdS - dU (2.49)

 

Интегрирование уравнения (2.49) при переходе системы из состояния 1 в состояние 2 при постоянных температуре и объёме даёт:

 

А ≤ T(S₂ – S₁) – (U₂ – U₁) (2.50)

 

или

A ≤ (U₁ – TS₁) – (U₂ – TS₂) (2.51)

 

Выражение в скобках назвали энергией Гельмгольца

 

U – TS = F (2.52)

 

Так как все величины, входящие в уравнение (2.52) являются функциями состояния, то и величина F также будет иметь свойства функции состояния системы. Тогда уравнение (2.51) примет вид:

 

А ≤ F₁ - F₂ = - ΔF (2.53)

 

Из уравнения (2.53) вытекает, что если процесс протекает обратимо при постоянных V и Т, то его работа максимальна и равна убыли энергии Гельмгольца (A = - ΔF). Для необратимых (самопроизвольных, неравновесных) процессов работа всегда меньше максимальной работы (A < - ΔF).

Энергия Гельмгольца может служить критерием направления протекания процесса и условия равновесия в системе при V = Const и T = Const. Продифференцируем уравнение (2.53)

 

dF = dU – TdS – SdT (2.54)

 

Из объединённого уравнения первого и второго законов термодинамики следует, что

 

TdS ≥ dU + PdV (2.55)

 

Подставив уравнение (2.55) в уравнение (2.54), получим:

 

dF ≤ dU – dU –PdV –SdT (2.56)

 

или

dF ≤ -PdV – SdT (2.57)

 

Уравнение (2.57) выражает зависимость изменения энергии Гельмгольца от объёма и температуры. При V = Const и T = Const уравнение принимает вид:

 

dF ≤ 0 (2.58)

 

Из уравнения (2.57) вытекает: в системе, находящейся при V = Const и

Т = Соnst, необратимые (самопроизвольные, неравновесные) процессы протекают с уменьшением энергии Гельмгольца (dF <0). По достижении минимального значения энергии Гельмгольца (dF = 0) в системе наступает состояние равновесия (рисунок 2.2)

 

F

А С

 

 

В

путь процесса

 

AB – необратимый, самопроизвольный процесс;

ВС – необратимый, несамопроизвольный процесс;

В – состояние равновесия

 

Рисунок 2.2 - Изменение энергии Гельмгольца при протекании

процесса системе при V = Const и T = Const.

 

Покажем, что функция F является характеристической функцией. Поскольку F является функцией состояния и зависит от объёма и температуры F = f(V,T), то она обладает полным дифференциалом:

 

dF = 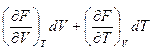(2.59)

 

С другой стороны для обратимого процесса зависимость энергии Гельмгольца от объёма и температуры имеет вид:

 

dF = - PdV – SdT (2.60)

 

Из свойств полного дифференциала и сравнения уравнений (2.59) и (2.60) следует:

 

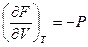и 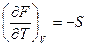(2.61)

 

Таким образом частные производные энергии Гельмгольца по объёму и температуре равны параметрам Р и S. Из равенства (2.61) следует, что давление есть мера убыли энергии Гельмгольца при увеличении объёма системы, в которой Т =Const. Энтропия есть мера уменьшения энергии Гельмгольца при увеличении температуры системы, находящейся при постоянном объёме.

 

2 .9 Энергия Гиббса, как критерий направления протекания