Можно указать 4 способа вычисления определенного интеграла:
1) по определению (как предел интегральной суммы)
2) приближенно (по формулам прямоугольников, трапеций, Симпсона)
3) по формуле Ньютона-Лейбница
4) используя программные пакеты (Matcad, и т.д.).
Примеры вычисления ОИ по определению и приближенно вы можете найти учебнике Н.С. Пискунова «Дифференциальное и интегральное исчисления». С использованием программных пакетов вы познакомитесь на занятиях по обще-специальным дисциплинам.
Мы рассмотрим вычисление ОИ по формуле Ньютона-Лейбница.
Теорема8.3.(Барроу)
Если f (х) непрерывна на отрезке [ a, b ], то для любого х Î[ a, b ] функция Ф(х)= 
дифференцируема на [ a, b ] и Ф¢(х) = f (х).
Доказательство. Как известно, если функция в любой точке заданного отрезка имеет производную, то она дифференцируема на этом отрезке. Найдем производную функции Ф(х) по определению: Ф¢(х) =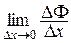 
. Рассмотрим приращение функции Ф(х):
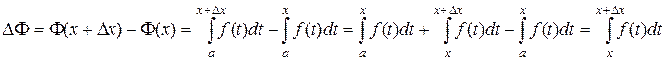
По теореме о среднем, " х Î[ a, b ] и "D х: х +D х Î[ a, b ] $ с Î [ x, х +D х ] такая, что
= f (с)D х. Так как f (х) непрерывна на отрезке [ a, b ], то при D х ® 0 имеем с ® х и f (с) ® f (х). Тогда
Ф¢(х) = =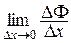 
,
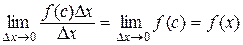т.е. производная функции Ф(х) существует на всем отрезке [ a, b ], значит эта функция дифференцируема на этом отрезке. Из последнего равенства так же видно, что " х Î[ a, b ] Ф¢(х) = f (х). ЧТД.
функцию Ф(х)= называют интегралом с переменным верхним пределом от функции f (х). Т.к. Ф¢(х)=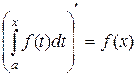 
, то функция
Ф(х)=
является первообразной для f (х) на отрезке [ a, b ]. Таким образом, из теоремы Барроу следует, что любая непрерывная на [ a, b ] функция имеет на этом отрезке первообразную и эта первообразная есть интеграл с переменным верхним пределом. Значит, мы фактически доказали теорему 14.2. темы «неопределенный интеграл» – достаточное условие существования первообразной.
Итак, согласно теореме Барроу, Ф(х)= есть первообразная для f (х) на отрезке [ a, b ]. Но все первообразные для заданной функции отличаются одна от другой лишь на константу, значит, если F(x) – другая первообразная функции f (х) на отрезке [ a, b ], то Ф(х) = F(x) + С, или
= F(x) + С.
Положим в этом равенстве х = а, получим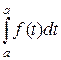 
= F(a) + С, или 0 = F(a) + С, откуда С = – F(a) и
= F(x) – F(a).
Если здесь положить х = b, получим
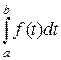= F(b) – F(a).
Эту формулу называют формулой Ньютона-Лейбница. Обозначим разность F(b) – F(a) =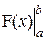 
и учитывая независимость определенного интеграла от переменной интегрирования, получим
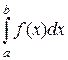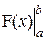= = F(b) – F(a).
Формула Ньютона-Лейбница дает простое и эффективное правило для вычисления определенного интеграла от непрерывной на заданном отрезке функции, позволяя свести вычисление предела интегральной суммы к отысканию первообразной от заданной функции и вычислению разности ее значений на концах отрезка интегрирования. Иначе говоря, определенный интеграл от заданной функции по заданному отрезку равен приращению первообразной для этой функции на заданном отрезке.
Замечание. Формула Ньютона-Лейбница применяется только для непрерывной функции f (х), первообразная для которой также непрерывна на заданном отрезке.
