5.1. Что такое алгебра логики?
| Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. |
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Что же такое логическое высказывание?
| Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo. |
 Джордж Буль
Джордж Буль
Так, например, предложение " 6 — четное число " следует считать высказыванием, так как оно истинное. Предложение " Рим — столица Франции " тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения " ученик десятого класса " и " информатика — интересный предмет ". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие " интересный предмет ". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа " в городе A более миллиона жителей ", " у него голубые глаза " не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
| Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. |
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание " площадь поверхности Индийского океана равна 75 млн кв. км " в одной ситуации можно посчитать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так, например, из элементарных высказываний " Петров — врач ", " Петров — шахматист " при помощи связки " и " можно получить составное высказывание " Петров — врач и шахматист ", понимаемое как " Петров — врач, хорошо играющий в шахматы ".
При помощи связки " или " из этих же высказываний можно получить составное высказывание " Петров — врач или шахматист ", понимаемое в алгебре логики как " Петров или врач, или шахматист, или и врач и шахматист одновременно ".
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В — высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" — логическая связка, А, В — логические переменные, которые мoгут принимать только два значения — "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием (или знаком 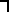 ). Высказывание
). Высказывание  истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна — спутник Земли " (А); " Луна — не спутник Земли " (
истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна — спутник Земли " (А); " Луна — не спутник Земли " ( ).
).
И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой ". " (может также обозначаться знаками  или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" — истинны.
ЕСЛИ-ТО Операция, выражаемая связками "если..., то", "из... следует", "... влечет...", называется импликацией (лат. implico — тесно связаны) и обозначается знаком  . Высказывание
. Высказывание  ложно тогда и только тогда, когда А истинно, а В ложно.
ложно тогда и только тогда, когда А истинно, а В ложно.
Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: "данный четырёхугольник — квадрат" (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание  , понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание
, понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание  истинно:
истинно:
- А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
- А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
- A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка "если..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США — демократ, то в Африке водятся жирафы", "если арбуз — ягода, то в бензоколонке есть бензин".
РАВНОСИЛЬНО Операция, выражаемая связками " тогда и только тогда ", " необходимо и достаточно ", "... равносильно...", называется эквиваленцией или двойной импликацией и обозначается знаком  или ~. Высказывание
или ~. Высказывание  истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
Высказывания А и В, образующие составное высказывание  , могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" (
, могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" ( ), "пингвины не живут в Антарктиде" (
), "пингвины не живут в Антарктиде" ( ). Образованные из высказываний А и В составные высказывания A
). Образованные из высказываний А и В составные высказывания A  B и
B и 

 истинны, а высказывания A
истинны, а высказывания A 
 и
и 
 B — ложны.
B — ложны.
Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию можно выразить через дизъюнкцию и отрицание:
А  В = В = 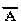 v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А  В = ( В = (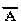 v В) . ( v В) . ( v А). v А).
|
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
5.2. Что такое логическая формула?
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
|
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B)  C. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
C. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
Как показывает анализ формулы (A v B)  C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v  , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А.  , которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо
, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо  обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом " 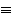 " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
5.3. Какая связь между алгеброй логики и двоичным кодированием?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
- одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
- на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
5.4. В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды?
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. Мы уже рассмотрели способы записи двоичной информации на магнитных дисках и на CD-ROM. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
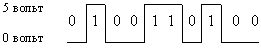
5.5. Что такое логический элемент компьютера?
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
5.6. Что такое схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ?
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1.
 Рис. 5.1
Рис. 5.1
Таблица истинности схемы И
| x | y | x. y |






