Задача №1. Двумерный закон распределения выручки X от реализации и затрат Y на производство продукции определяется плотностью вероятности:
(1)
Определить МОЖ и СКО выручки X и затрат Y на производство продукции, коэффициент корреляции 
данных СВ. Записать уравнение регрессии затрат на выручку от реализации продукции.
Решение. По виду приведенной двумерной плотности вероятности можно сделать вывод о том, что СВ Х и У имеют нормальный закон распределения, двумерная плотность вероятности которого определяется формулой (№4.1 лекции №14).
 |
(2)
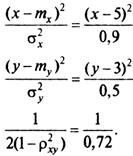Из сравнения формул (1) и (2) можно выписать равенства, из которых очень просто определяются математические ожидания, дисперсии и коэффициент корреляции случайных величин Х и У:
(3)
Из данных равенств (3) следует, что математическое ожидание выручки от реализации и затрат на производство продукции соответственно равно тх = 5, ту = 3.
Среднее квадратичное отклонение выручки 
и затрат 
на производство продукции соответственно равно 
Для коэффициента корреляции (см. 3-е уравнение системы уравнений 3) случайных величин Х и Y получим:
 |
(4)
Уравнение регрессии затрат на производство У и на выручку от реализации продукции X определяется формулой (№4.11 см.лекцию №14):
 |
(5)
Тогда для рассматриваемого примера уравнение регрессии может быть записано в виде:
 |
(6)
График уравнения регрессии затрат на производство Y и на выручку от реализации продукции X приведен на рис. 1.1.
 |
Рис.1.1 График уравнения регрессии
Из графика и полученного уравнения следует, что для увеличения выручки от реализации продукции X необходимо увеличивать затраты на ее производство Y.
При увеличении затрат на одну денежную единицу 
можно с наибольшей вероятностью ожидать, что выручка от реализации продукции возрастет на 
1,073 денежных единиц (см. уравнение 6).
Задача №2. Найти вероятность попадания СВ (X; Y) в прямоугольник, ограниченный прямыми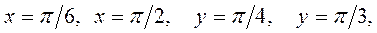 
если известна функция распределения:
(1)
Решение. Для решения данной задачи необходимо использовать формулу по вычислению вероятности попадания СВ Х и У в заданную прямоугольную область:
 |
(2)
С целью обеспечения удобства пользования данной формулой введём следующие обозначения: 
(3)
Тогда выражение (2) с учётом (3) можно записать в следующем виде:
(4)
Подставив в формулу (4), заданные по условию задачи значения границ случайных величин X и Y, а именно: 
получим:
 |
Задача №3. Найти плотность совместного распределения f(x,у) системы СВ X, У (X – доход инвестиционной компании от приобретённых акций, Y – цена приобретения акций этой компанией) по известной функции распределения:
(1)
Решение. По определению плотности совместного распределения системы двух непрерывных СВ, можно записать:
 |
(2)
Так как искомая плотность распределения, является второй частной производной от функции распределения (см. уравнение 2), то, поэтому, найдем вначале частную производную по x (см. приложение №1 метод.разработки), заданной уравнением (1) функции распределения:
 |
(3)
От полученного результата (3) найдём частную производную по у, что позволяет в итоге получить искомую плотность совместного распределения x и y:
(4)
Задача №4. 
Известно, что число оборотов кредита банка X зависит от оборота кредита по погашению Y в соответствии с плотностью их совместного распределения вида:
(1)
Найти функцию распределения заданной двумерной СВ X и Y.
Решение. Для нахождения двумерной функции распределения системы СВ 
воспользуемся свойством №2 плотности распределения системы двух СВ:
 |
(2)
Подставив в выражение (2) заданную плотность распределения выражением (1), используя таблицу основных интегралов, (см. Приложение №2) получим:
 |
(3)
Задача №5. Плотность распределения системы 2-х непрерывных СВ X (себестоимость продукции предприятия) и Y (объём реализованной продукции), которые определяют валовую прибыль предприятия, описывается следующим выражением:
 |
(1)
Найти вероятность попадания случайной точки в прямоугольник (рис. 1.2) с вершинами К (1; 1), L(
; 1), M(1; 0) и N (;0).Координаты точек выражены в млн. рублей.
Рис.1.2Прямоугольник для задачи №5
Решение.
Известно, что вероятность попадания 2-х СВ в прямоугольную область а < Х< b и с < Y< d, в том числе и в произвольную область D, которая может быть разбита «n» элементарных прямоугольников, можно определить путем вычисления двойного интеграла вида (выражение 3.5 лекции №14):
(2)
где - 
Тогда искомая вероятность определится следующим образом:
 |
Задача №6. 
Двумерная СВ (X, У) задана плотностью совместного распределения вида:
(1)
Найти плотности распределения составляющих X и У.
Решение.
Для нахождения плотностей распределения составляющих X и Y, необходимо использовать следующее правило: Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.
В соответствии с данным правилом можно записать две следующие формулы:
(2)
(3)
Используя формулу (2), найдём плотность распределения составляющей X, но для этого вначале, применяя условия системы двух уравнений (1), определим реальные пределы интегрирования для интеграла по вычислению 
:
так как 
Иначе это неравенство можно записать в виде:
или пределы интегрирования для формулы (2) в условиях задачи равны:
Тогда, в соответствии с условиями задачи и формулы (2) по вычислению интересующей нас одномерной плотности распределения составляющей X, для первого уравнения системы (1) можно записать:
(4)
Правая часть полученного выражения (4) имеет смысл, лишь тогда, когда подкоренное выражение имеет значение больше нуля, т.е. 
, а следовательно, должно выполняться неравенство вида: 
Таким образом, искомое выражение интересующей нас одномерной плотности распределения составляющей X, будет иметь вид следующей системы двух уравнений:
(5)
Аналогично рассуждая и применяя формулу (3), можно найти плотность распределения составляющей Y (выполнить студентам самостоятельно):
 |
(6)
