В резервированной системе отказ какого-либо элемента не обязательно приводит к отказу всей системы. Типичным случаем является логически параллельное соединение элементов (рис.5), при котором система отказывает тогда, когда отказывают все ее элементы. Такой тип резервирования называют постоянным или нагруженным m-кратным резервированием. В этом случае все элементы выполняют одну и ту же функцию, работают одновременно и равнонадежны. По теореме умножения вероятностей имеют место следующие выражения:
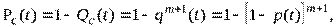
где q(t), p(t) – соответственно вероятности отказа и безотказной работы одного элемента.
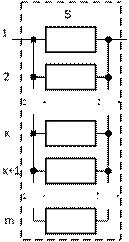
Рисунок. 5. Схема логического соединения элементов резервированной системы
Если для элементов справедлив экспоненциальный закон распределения надежности, то
.
Для высоконадежных систем, у которых lt<0,1 и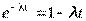 
, имеем
Среднее время наработки до отказа резервированной системы:
,
где 
- среднее время наработки до отказа основной системы или любой из резервных систем.
Кроме m-кратного резервирования (m целое число) используют также резервирование с дробной кратностью, которое называют логическим соединением «k из n». Это означает, что система работоспособна, если работоспособны не менее k элементов. На рис.5,б приведена структурная схема «k из n» с кратностью резервирования m =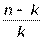 
.
Универсальным методом расчета надежности любой резервированной системы со сложной логической структурой является метод полной группы событий. В момент времени t состояние системы S может быть задано двоичным вектором A(t) = 
, где Эi(t)=1, если в момент t i-й элемент работоспособен, и Эi(t)=0, если к этому моменту он уже отказал. Всего существует 2n состояний, которые образуют полную группу событий. Пусть надо рассчитать вероятность безотказной работы P(t) системы «2 из 3». Все возможные состояния этой системы приведены в табл.3.1
Таблица 3.1
Состояния системы «2 из 3»
| Аi | Э1 | Э2 | Э3 | S | R |
| А0 | (1-p1)(1-p2)(1-p3) | ||||
| А1 | (1-p1)(1-p2)p3 | ||||
| А2 | (1-p1)p2(1-p3) | ||||
| А3 | (1-p1)p2p3 | ||||
| А4 | p1(1-p2)(1-p3) | ||||
| А5 | p1(1-p2)p3 | ||||
| А6 | p1p2(1-p3) | ||||
| А7 | p1p2p3 |
B столбце R указаны вероятности событий Аi, причем сумма всех этих вероятностей равна 1. В результате появления событий Аi, система S может оказаться работоспособной в момент времени t (S=1) или неработоспособной (S=0).
Таблица задает некоторую функцию алгебры логики S=f(Э1, Э2, Э3). Таким образом, надежность сложной системы есть функция алгебры логики от надежности ее элементов. В данном примере эта функция есть известная мажоритарная функция. Очевидно, что вероятность безотказной работы системы будет равна сумме вероятностей тех событий Аi, для которых S=1:
.
Для данных таблицы
Если все элементы структуры равнонадежны (p1 = р2 = p3 = p), то
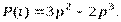
Метод полной группы событий применим в любом случае, однако для систем с большим числом элементов он становится слишком громоздким из-за большого числа состояний. Задача упрощается для широкого класса систем с последовательно-параллельной структурой. В таких системах элементы соединяются только последовательно или параллельно. В таком случае применяют метод преобразования структурной схемы (метод свертки), объединяя элементы в более крупные блоки и применяя формулы расчета для элементарных схем надежности (рис.6).
Рисунок 6. Преобразование структурной схемы надежности
Для элементарных схем функции надежности соответственно равны
- для последовательного соединения;
- для параллельного соединения.
Вероятность безотказной работы системы с последовательно-параллельной структурой, изображенной на рис.7,а наиболее удобно выразить постепенным упрощением ее схемы. Заменим сначала параллельные
Рисунок 7. Этапы последовательного упрощения последовательно-параллельной структуры
подсистемы 2 и 3 новой подсистемой 23 (рис.7,б). Тогда вероятность безотказной работы новой подсистемы
Теперь заменим последовательные подсистемы 1 и 23 новой подсистемой 123 (рис.5,в). Тогда вероятность безотказной работы этой подсистемы
.
Далее заменим последовательные подсистемы 4 и 5 одной подсистемой 45 с вероятностью безотказной работы
Наконец, заменив параллельные подсистемы 123 и 45 новой подсистемой 12345 (рис.5,г) получим вероятность безотказной работы этой подсистемы
что соответствует вероятности безотказной работы системы.
Часто не требуется знать точное значение вероятности безотказной работы, а достаточно только оценить эту величину снизу и сверху. Тогда можно применить приближенный метод минимальных путей и сечений. Рассмотрим этот метод на примере вычислительной системы (рис.8,а).
Рисунок 8. Схема расчета надежности вычислительной системы
Она состоит из вычислительных блоков 1, 2 (источники информации) 6, 7 (приемники информации) и трех устройств сопряжения 3 – 5. Система работоспособна, если существует путь передачи информации хотя бы от одного источника к одному, по крайней мере, приемнику. Структурная схема расчета надежности системы в виде графа представлена на рис.8,б. Вершины графа соответствуют элементам системы, а дуги – связям между ними. Вершины M и N называют полюсами. Отказ элемента соответствует обрыву ребер, которые с ним связаны, а отказ всей системы соответствует нарушению связи между полюсами.
Множество элементов системы называется путем А, если при их исправности система работоспособна независимо от состояния других элементов. Им соответствуют все пути между полюсами в графе надежности. Путь называется минимальным, если никакое его подмножество не является путем. Граф (рис.8,б) имеет шесть минимальных путей: 1-3-6, 1-4-6, 1-4-7, 2-4-6, 2-4-7, 2-5-7. Множество элементов системы называется сечением В, если отказ всех этих элементов приводит к отказу системы независимо от состояния других элементов. У минимального сечения никакое его подмножество не является сечением. Рассматриваемый граф имеет девять минимальных сечений: 1-2, 6-7, 1-4-5,1-4-7, 2-3-4, 2-4-6, 3-4-5, 3-4-7, 4-5-6.
Нижняя граница надежности Pн(t) определяется как вероятность безотказной работы гипотетической последовательно-параллельной системы, составленной из последовательно включенных групп элементов, соответствующих всем минимальным сечениям (рис.8,в), а верхняя граница Pв(t) – системы из параллельно включенных групп элементов, соответствующих всем минимальным путям (рис.8,г). Таким образом,
где n, m – число путей и сечений системы; P(Ai), P(Bj) – соответственно вероятности событий Ai и Bj.
