2.3.1 Последовательное соединение из N восстанавливаемых элементов. Здесь следует отметить, что предлагаемые формулы, по которым определяются количественные характеристики показателей надежности систем электроснабжения, соответствуют экспоненциальному закону распределения случайных величин.
Пусть система электроснабжения состоит из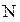 
последовательно соединенных элементов (рисунок 2.17).
 |
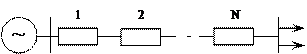Рисунок 2.17
Средняя вероятность безотказной работы системы
.
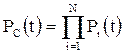Средняя вероятность отказового состояния системы
- 
,
= 
.
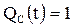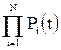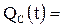
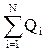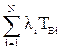Интенсивность (параметр потока) отказов системы
.
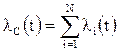Среднее время безотказной работы или наработка на отказ системы
.
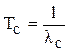Среднее время восстановления системы
.
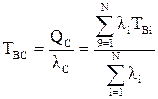Если все элементы системы одинаковы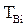 
= 
= 
; 
= 
= 
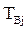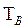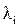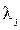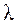, то:
= 
.
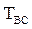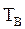Если учитываются преднамеренные отключения элементов с параметром потока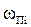 
и средним временем 
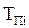, то интенсивность отказов и вероятность отказа системы определятся выражениями:
+ 
;
,
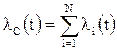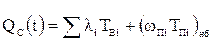где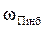 
и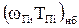 
- соответственно наибольшие значения параметра потока и вероятности преднамеренных отключений.
2.3.2 Параллельное соединение из N восстанавливаемых элементов. Пусть система электроснабжения состоит из параллельно соединенных элементов (рисунок 2.18)
Под отказом системы понимается отсутствие напряжения на шинах рассматриваемого узла нагрузки, т.е. не учитывается ограничение по пропускной способности элементов
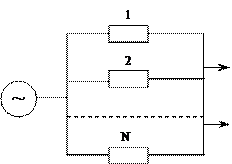
Рисунок 2.18
Вероятность безотказной работы системы
= 
.
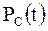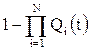Вероятность отказа системы
.
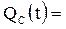
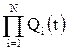Интенсивность (параметр потока) отказов системы
.
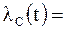
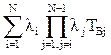Среднее время безотказной работы (наработка на отказ) системы
.
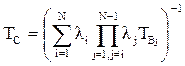Среднее время восстановления системы
= 
.
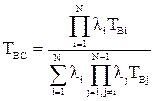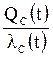Если учитываются преднамеренные отключения с параметром потока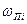 
и средним временем 
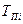, то интенсивность отказа системы
+ 
,
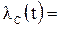
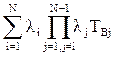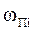
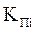
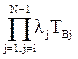где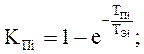 
.
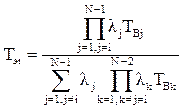Вероятность отказа системы с учетом преднамеренных отключений определится из выражения:
.
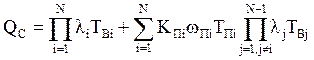Примеры расчета показателей надежности систем электроснабжения
В заключении рассмотрим несколько примеров расчета параметров надежности восстанавливаемых систем электроснабжения.
Задача 1. Система электроснабжения состоит из повышающего трансформатора Т1, линии электропередачи Л и понижающего трансформатора Т2 (рисунок 41).
Определить параметр потока отказов системы, среднюю вероятность отказа, среднее время восстановления (преднамеренные отключения не учитываются).
Дано:
Т1 Л Т2
~
Рисунок 2.19– Система электроснабжения
| Т1 | Л | Т2 | |
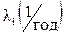
| 0,02 | 0,125 | |
|
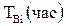
Решение.
Интенсивность (параметр потока) отказов системы:
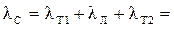0,02+0,12+0,025=0,165 
.
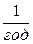Средняя вероятность отказа:
= 
=
= 
= 
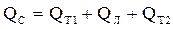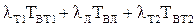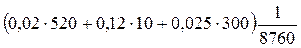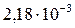
Среднее время восстановления
= 
,
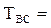
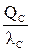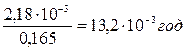или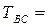 
Задача 2. Определить параметр потока отказов системы, среднюю вероятность отказа и время восстановления, если потребитель электроэнергии (ПЭ) получает питание по двум параллельным линиям электропередачи (рисунок 2.20).
Дано:
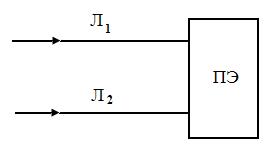
Рисунок 2.20
| Л1 | Л2 | |
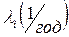
| 0,03 | 0,04 |
|
Интенсивность (параметр потока) отказов системы:
= 
=
= 
= 
.
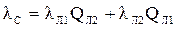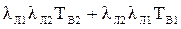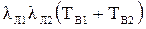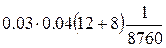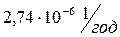Средняя вероятность отказа системы:
= 
= 
.
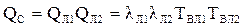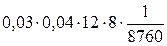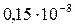Среднее время восстановления:
= 
.
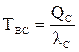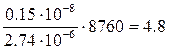
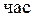Задача 3. Решить предыдущую задачу при условии, что параметр потока преднамеренных отключений первой линии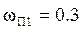 
, 
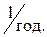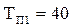
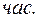, а второй линии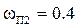 
, 
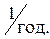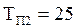
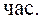
Предварительно определяем коэффициенты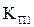 
и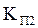 
:
= 
= 
.
= 
= 
.
+ 
=
= 
=
= 
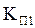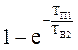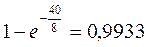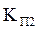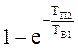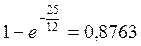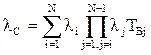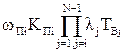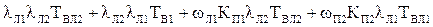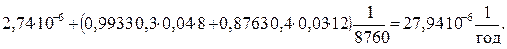
Средняя вероятность отказа системы:
=
= 
= 
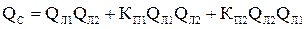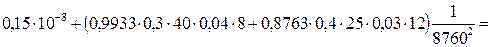
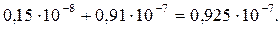
Среднее время восстановления системы:
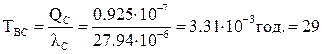
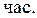
Учет преднамеренных отключений элементов резервированных систем существенно увеличивает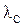 
и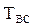 
.
