31. Изоморфны ли данные графы? Ответ обоснуйте.
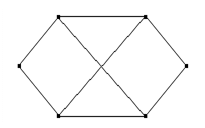

а) G 1 G 2


б) H 1 H 2
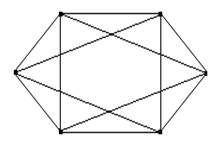

в) G 3 G 4

 г) H 3 H 4
г) H 3 H 4
32. Исследуйте данные тройки графов на попарную изоморфность.
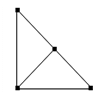

 а) G 1 G 2 G 3
а) G 1 G 2 G 3

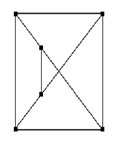

б) Н 1 Н 2 Н 3

в) G 4 G 5 G 6
33. Пусть связные графы G и H имеют по 6 вершин и по 8 ребер. У графа G ровно 2 вершины степени 2, а граф Н имеет ровно 4 вершины степени 3. Можно ли утверждать, что графы G и H
а) изоморфны? б) не изоморфны?
34. Сколько существует попарно неизоморфных графов с
а) 16 вершинами и 118 ребрами? б) 16 вершинами и 117 ребрами?
|
 G: H:
G: H:
36. Составьте коды для данных деревьев:

 Т 1 Т 2
Т 1 Т 2
37. Даны коды деревьев:
а) (0100011001101011); б) (00101001110001010111).
Сколько вершин имеет каждое из этих деревьев? Постройте соответствующие деревья.
38. Докажите, что в каждом дереве есть не менее двух листьев.
39. Сколько существует неизоморфных между собой деревьев с 6 вершинами?
40. Сколько ребер имеет лес с p вершинами и n деревьями?
41. Докажите, что графы G и H не содержат циклов нечетной длины. Составьте для каждого из них матрицу Кирхгофа.

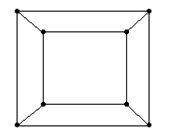 G: H:
G: H:
42. Завуч школы должен составить расписание одного учебного дня для одного класса (все 4 предмета в расписании должны быть разные) с учетом следующих обстоятельств:1. учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;2. учитель литературы может дать один - либо второй, либо третий урок;3. математик готов дать либо только первый, либо только четвертый урок;4. преподаватель физкультуры согласен дать только третий или четвертый уроки. Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч?
43. Приведите пример связного графа с циклами, который является
а) эйлеровым, но не гамильтоновым; б) гамильтоновым, но не эйлеровым;
в) не эйлеровым, и не гамильтоновым.
44. Доказать, что в любом полном графе, имеющем не менее 3 вершин, есть гамильтонов цикл.
45. Доказать критерий полуэйлеровости графа: связный граф G обладает эйлеровой цепью в том и только том случае, если он имеет ровно 2 вершины нечетной степени.
46. Доказать, что если граф G является гамильтоновым, то в нем отсутствуют разделяющие вершины (это необходимое условие гамильтоновости графа).
47. Показать, что в пронумерованном полном графе Kp имеется (p- 1)!/2 различных гамильтоновых циклов.

48. Существуют ли в полном двудольном графе K 3,3 и в графе G, заданном на рисунке, эйлеров цикл, гамильтонов цикл, эйлерова цепь, гамильтонова цепь? Укажите их или докажите их отсутствие.
G:
49. Показать, что граф, у которого имеются 2 несмежные вершины 3-ей степени, а остальные имеют степень не большую, чем 2, не обладает гамильтоновым циклом.
50. Является ли данный граф гамильтоновым?
|
51. Докажите, что любой граф с р вершинами, имеющий не менее  ребер, имеет гамильтонов цикл.
ребер, имеет гамильтонов цикл.
Занятие 4. Планарные графы. Раскраска графов
|
|
а) G 1: б) G 2:
|
 в) H: г) P – граф Петерсена:
в) H: г) P – граф Петерсена:
53. Докажите, что в любом планарном графе существует вершина, степень которой не больше 5.
54. У графа G с р вершинами ( ) только 1 пара вершин не соединена ребром (все остальные вершины смежные). При каком р граф G является планарным? Будет ли планарным граф, полученный из К 6 удалением двух ребер?
) только 1 пара вершин не соединена ребром (все остальные вершины смежные). При каком р граф G является планарным? Будет ли планарным граф, полученный из К 6 удалением двух ребер?
55. Плоский связный граф, каждая грань которого, включая и внешнюю, ограничена циклом длины 3, называется триангуляцией. Покажите, что всякая триангуляция с  вершинами имеет 3 р -6 ребер и 2 p -4 граней.
вершинами имеет 3 р -6 ребер и 2 p -4 граней.
56. Докажите, что в любом планарном графе, имеющем не менее 4 вершин, найдутся по меньшей мере 4 вершины степени не больше 5.
57. Найдите хроматические числа и хроматические индексы графов G 1 и G 2, а также графов Н и Р из задачи 52.

 G 1 G 2
G 1 G 2
58. Докажите неравенство для хроматического числа графа  .
.
Занятие 5. Ориентированные графы
59. Даны орграфы. Составьте для каждого из них матрицу смежности, матрицу инцидентности, матрицу достижимости. Каковы максимальная полустепень исхода и минимальная полустепень захода в этих орграфах? Являются ли эти орграфы направленными? Есть ли в них источники или стоки?

 D 1 D 2
D 1 D 2
60. Какое бинарное отношение соответствует
а) неориентированному псевдографу без кратных ребер; б) турниру?
61. Являются ли бинарные отношения, соответствующие орграфам из задачи 59, рефлексивными, антирефлексивными, симметричными, антисимметричными, транзитивными, линейными?
62. Верно ли, что в полном орграфе всегда существует источник?
63. Докажите, что в любом турнире существует гамильтонов путь.
64. Докажите, что если в орграфе D отсутствуют вершины с нулевыми полустепенями исхода и захода, то в D имеется простой контур.
65. Докажите, что в бесконтурном орграфе существует вершина с нулевой полустепенью исхода или захода.
66. Определите, имеют ли контуры орграфы с матрицами смежности:


 .
.
Выясните, являются ли эти орграфы слабо связными, односторонне связными или сильно связными. Составьте для них матрицы достижимости и сильной связности.
67. Дляорграфов D и H, заданных матрицами смежности, найдите матрицы сильной связности, количество компонент сильной связности и матрицы смежности этих компонент. Постройте графические изображения данных орграфов и их компонент сильной связности.
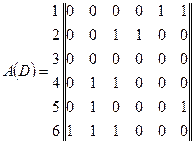
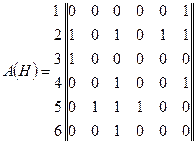
Занятие 6. Экстремальные задачи и алгоритмы на графах
68. Для графов G и H найдите наибольшие независимое множество вершин и паросочетание, наибольшую клику, а также наименьшие вершинное и реберное покрытия.
G: H:

|

69. Найдите минимальный маршрут из 1-й вершины в 6-ую в орграфе D, заданном матрицей смежности, а также из вершины 5 в вершину 7 в неориентированных графах G и H:
 G H
G H


70. Пользуясь соответствующим алгоритмом, найдите эйлеров цикл или эйлерову цепь в мультиграфах, заданных матрицами смежности.

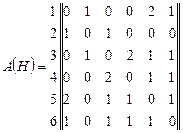
 71. Пользуясь алгоритмами Прима и Краскала, построить остов минимального веса для графа
71. Пользуясь алгоритмами Прима и Краскала, построить остов минимального веса для графа
72. Пользуясь алгоритмом Дейкстры, определите минимальный путь из v 1 в v 6 в нагруженных орграфах, заданных матрицами весов.
а) б)
| v 1 | v 2 | v 3 | v 4 | v 5 | v 6 | v 1 | v 2 | v 3 | v 4 | v 5 | v 6 | |||
| v 1 | ¥ | ¥ | ¥ | v 1 | ¥ | ¥ | ||||||||
| v 2 | ¥ | ¥ | v 2 | ¥ | ¥ | ¥ | ||||||||
| v 3 | ¥ | ¥ | ¥ | v 3 | ¥ | ¥ | ¥ | ¥ | ||||||
| v 4 | ¥ | ¥ | ¥ | ¥ | v 4 | ¥ | ¥ | ¥ | ¥ | |||||
| v 5 | ¥ | ¥ | ¥ | ¥ | v 5 | ¥ | ¥ | ¥ | ¥ | |||||
| v 6 | ¥ | ¥ | ¥ | ¥ | v 6 | ¥ | ¥ | ¥ |
73. Пользуясь алгоритмом Дейкстры, определите минимальный путь из v 1 в v 7 в нагруженных орграфах, заданными матрицами весов.
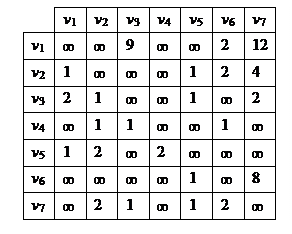
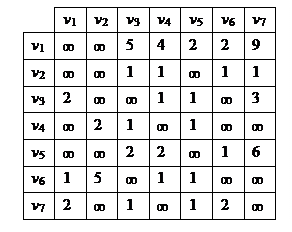 а) б)
а) б)
74. Пользуясь алгоритмом Флойда, найдите кратчайшие пути между всеми парами вершин в орграфах, заданных матрицами весов.

 а) б)
а) б)











