ТЕОРИЯ КОНЕЧНЫХ ГРАФОВ И ЕЕ ПРИЛОЖЕНИЯ
Занятие 1. Способы задания графов. Основная теорема теории графов.
Операции над графами.
1. Даны графы G и H:
а) Составьте для каждого из них списки вершин и ребер (в виде таблицы), а также матрицы смежности, инцидентности, векторов смежности. Определите по этим матрицам минимальную, максимальную и среднюю степени вершин данных графов.
б) Из матрицы смежности для данных графов получите аналогичные матрицы для дополнений к этим графам, и по ним восстановите графы 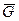 и
и  .
.
| |||
| |||
G: H:
2. По матрице инцидентностиопределите минимальную, максимальную и среднюю степени вершин графа G. Не изображая этот граф в виде диаграммы, составьте список его вершин и ребер, а также матрицы смежности и векторов смежности.
x 1 x 2 x 3 x 4 x 5 x 6 x 7

4. N человек (N >2) проводят шахматный турнир в один круг. К некоторому моменту выясняется, что в точности двое сыграли одинаковое число партий. Докажите (переведя условие задачи на язык графов), что либо в точности один участник еще не сыграл ни одной партии, либо ровно один сыграл все партии.
5. Существуют ли графы со следующими наборами степеней вершин:
а) {2, 3, 3, 2, 3}; б) {1, 2, 3, 4}?
Если существуют, то изобразите их графически.
6. Сколько рёбер имеет полный граф с p вершинами?
7. Сколько рёбер имеет регулярный граф с p вершинами степени r?
8. Сколько рёбер может быть у регулярного графа с 9 вершинами?
9. Докажите, что каждый кубический граф имеет чётное число вершин.
10. Сколько вершин может быть у графа с 4 ребрами, если петли, кратные ребра и изолированные вершины у него отсутствуют?
11. Найти объединение, пересечение и разность двух графов.
 а)
а)
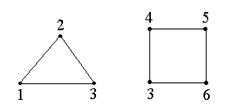
б)
 в)
в)
12. Составьте матрицы смежности для графовG1ÈG2, G1ÇG2, G1\G2, если


а) 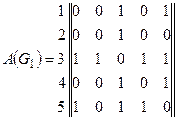


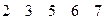
б) 

Занятие 2. Маршруты, цепи и циклы в графах.
Связность графов. Расстояния в графе.
 13. Дайте классификацию маршрутов в графе,
13. Дайте классификацию маршрутов в графе,
приведенном на рисунке 1.
(1, 2, 3, 5, 2);
(2, 3, 5, 4);
(2, 3, 4, 5, 3, 2);
(3, 4, 5, 3).
Рис. 1.
14. Приведите примеры замкнутого пути, простого цикла и цикла, не являющегося простым, в графах G и H из задачи 1.
15. Дан регулярный граф с 6 вершинами и 9 ребрами.
а) Докажите, что в нем есть хотя бы 1 цикл.
б) Нарисуйте этот граф.
в) Каковы обхват и периметр данного графа?
г) Сколько в этом графе циклов наименьшей длины?
16. Докажите, что всякий замкнутый маршрут нечётной длины содержит простой цикл. Верно ли аналогичное утверждение для маршрутов чётной длины?
17. Докажите, что каждый граф G содержит цепь длины  и (при условии, что
и (при условии, что  ) цикл длины не менее
) цикл длины не менее 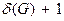 .
.
18. Найдите количество маршрутов длины 3 от i -ой вершины к j -ой при всех i, j =1,…,5 в графе G 1 (а) из задачи 12.
19. Докажите, что в связном графе любые две простые цепи максимальной длины имеют, по крайней мере, одну общую вершину. Верно ли, что они всегда имеют общее ребро?
20. Пусть р – число вершин, q – число ребер, k – число компонент связности графа. Докажите, что тогда имеет место следующее неравенство:  .
.
21. Пусть граф G имеет р вершин. Доказать, что если минимальная степень его вершин  , то граф связен.
, то граф связен.
22. Сколько компонент связности имеет граф G? Составьте для него матрицу смежности в блочно-диагональном виде (каждой компоненте связности должен соответствовать определенный блок).

G:
 23. Найдите все мосты и разделяющие вершины в графеG:
23. Найдите все мосты и разделяющие вершины в графеG:
G:
24. Доказать, что всякий нетривиальный связный граф содержит не менее двух вершин, не являющихся разделяющими.
25. Докажите, что ребро (v, w) в графе G является мостом тогда и только тогда, когда в этом графе существуют 2 вершины u 1и u 2 такие, что каждая цепь, соединяющая их, проходит через вершины v и w.
26. Докажите неравенство 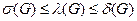 , где
, где  - вершинная связностьграфа G,
- вершинная связностьграфа G, 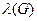 - реберная связность,
- реберная связность,  - минимальная степень вершины графа.
- минимальная степень вершины графа.
27. Найдите радиус, диаметр и центр
а) графа G из задачи 23; б) графа Н 4 из задачи 31.
28. Докажите, что для любого графа G  .
.
29. Докажите, что для каждого графа G, содержащего цикл, справедливо неравенство:  , где
, где 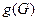 - длина наименьшего цикла в графе G.
- длина наименьшего цикла в графе G.
30. Докажите, что в графе G радиуса не более k с максимальной степенью вершины не более d имеется не более  вершин.
вершин.
Занятие 3. Изоморфизм графов. Разрезы в графе. Деревья.








