После построения и заполнения таблиц выборочными данными приступают к их числовому описанию. Определяют объем – количество данных и диапазон изменения случайной величины в выборке – разницу между максимальным и минимальным значением в выборке (размах). Для построения гистограммы – выборочного (статистического) образа функции плотности вероятности диапазон изменения случайной величины размечается на интервалы (карманы) и запускается процедура сортировки данных, которая отмечает частоты – числа попаданий данных из выборки в соответствующие карманы и строит соответствующее графическое изображение. Различают абсолютные и относительные частоты. Последние определяются как числа попаданий в интервалы-карманы, деленные на объем выборки (общее количество данных). Сумма относительных частот в гистограмме равна 1, а сами относительные частоты могут быть выражены в процентах.
Назначение карманов чаще всего эквидистантное, т.е. с равным шагом. Эмпирическое правило выбора шага – в каждый карман должно попадать не менее 5 выборочных значений. Например, если минимальное значение в выборке равно 10, максимальное – 100, а объем выборки равен 80, то следует назначить не более 80/5 = 16 карманов; выберем число карманов 15 в диапазоне [10,100] с равным шагом в (100 – 10)/15 = 6, тогда границы интервалов карманов задаются числами 10, 16, 22, …. 94, 100.
Для построения выборочного образа функции распределения вероятности – диаграммы накопленных частот, данные гистограммы относительных частот суммируются по всем предыдущим карманам в каждый следующий интервал-карман.
Для вычисления частотных распределений и построения графических изображений гистограмм и полигонов частот (тип представления выборочного распределения, в котором точки, соответствующие высотам столбиков гистограммы, соединены ломаной линией) в пакете анализа MS Excel применяется утилита
Гистограмма. Используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного интервала. Например, необходимо выявить тип распределения успеваемости в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и количества студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей.
Гистограммы и полигоны частот позволяют визуально оценить принадлежность выборки тому или иному типу модельного вероятностного распределения.
Описательная статистика. Служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных. Определяются Среднее, Стандартная ошибка (среднего), Медиана, Мода, Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность, Интервал, Минимум, Максимум, Сумма, Счет, Наибольшее значение, Наименьшее значение и Уровень надежности выборки.
Здесь и далее для обозначения случайных величин используются заглавные буквы латинского алфавита, горизонтальная черта над символом означает среднее значение величины. Символы 
и 
обозначают соответственно математическое ожидание (среднее генеральной совокупности) и стандартное отклонение. Объем выборки (количество данных в выборке) представлен функцией Счет и обозначается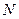 
.
В результате статистического анализа выборки с помощью описательной статистики мы получаем точечные или интервальные оценки параметров генеральной совокупности.
Точечные оценки представляются одним числом. Следующие оценки параметров являются точечными.
Сумма вычисляется суммированием всех выборочных данных с учетом знаков и обозначается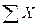 
.
Наименьшее и Наибольшее значение обозначаются, соответственно, как 
и 
.
И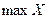нтервал (размах) выборки определяется как разность между наибольшим и наименьшим значениями - .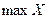
Среднее (арифметическое) данных выборки вычисляется по формуле:
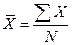
Стандартная ошибка среднего (редко используется по причине сложности использования в дальнейших вычислениях) определяется формулой:
Стандартное отклонение данных выборки (от среднего) вычисляется по формуле
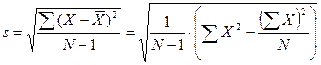
Дисперсия данных выборки определяется как 
.
Минимум и Максимум определяют соответственно минимальную и максимальную частоты, зафиксированные описательной статистикой в заданных интервалах анализа.
Мода – статистика, определяемая как наиболее часто встречающееся значение. Различают типы формы распределения: «одногорбое» – унимодальное, «двугорбое» – бимодальное и т.д.
Асимметрия – статистика, характеризующая несимметричность формы распределения слева и справа от линии среднего. Эталоном симметрии служит нормальное распределение.
Эксцесс – статистика, определяющая степень отличия остроты пика формы одномодального (имеющего только один максимум) распределения от нормального распределения.
Следует подчеркнуть, что точечная оценка является случайной величиной, поскольку ее значение отличается в различных выборках при наблюдении случайного явления. Точечная оценка называется несмещенной, если при повторных случайных выборках из генеральной совокупности среднее по всем выборкам значение оценки стремится к оцениваемому параметру генеральной совокупности с увеличением числа выборок.
Интервальные оценки представляются парой чисел (границами некоторого интервала); интервальные оценки даются вместе с вероятностью или уровнем надежности (доверия ) (попадания оцениваемой величины в указанный доверительный интервал).
Уровень надежности – вероятность того, что истинное значение оцениваемой статистики находится в построенном (чаще всего на основе точечной оценки) доверительном интервале. Уровень надежности часто задается в процентах.
Часто возникает необходимость группирования и/или ранжирования данных. Уже в результате построения гистограммы данные оказываются сгруппированными – принадлежащими определенным интервалам (классам). Из гистограммы и полигона частот для каждого класса становятся известными соответственно частота и кумулятивная (накопленная) частота. Суммируем частоты в интервалах до и в интервалах после указанного класса и определим соответствующие процентные доли в отношении суммы всех частот – получим проценты данных, лежащих ниже и выше указанного класса; отношение частоты класса к сумме всех частот дает, очевидно, процент данных, принадлежащих классу; сумма найденных процентных значений равна 100%. Стандартными группами, формируемыми в статистике, являются персентили (процентильные ранги),децили, квартили и т.п. Персентиль (процентиль) – число, указывающее какой процент данных лежит ниже или выше указанного значения. Для вычисления персентиля используется формула
где L% – процент данных, лежащих ниже указанного (критического) интервала; I% – процент данных, принадлежащих указанному интервалу; LRL – нижняя реальная граница указанного интервала; h – размер (шаг) интервала; score – значение, для которого определяется персентиль. Каждый 10-ый персентиль называется децилем, каждый 25-ый квартилем (второй квартиль соответствует медиане). Обратная процедура – вычисление выборочного значения по заданному процентному рангу – считается по формуле
где 
– частота критического класса (интервала), которому принадлежит значение; SFB – сумма частот классов, лежащих ниже критического; SF – сумма всех частот.
В MS Excel соответствующие процедуры включены в утилиту пакета анализа
Ранг и персентиль. Используется для вывода таблицы, содержащей порядковый и процентный ранги для каждого значения в наборе данных. Данная процедура может быть применена для анализа относительного взаиморасположения данных в наборе.
Для получения удобных представлений используют перенормировки данных. Ряд перенормировок исторически связан с использованием статистических таблиц. Так, например, таблицы нормального распределения приводятся стандартно для 
и 
. Для того, чтобы привести экспериментальные данные форме, допускающей применение стандартных статистических таблиц, со случайной величиной следует выполнить формальное преобразование:
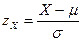
при неизвестных и они заменяются соответственно 
и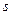 
.
