Случайная величина и вероятность события
Понятие вероятности
Алгебра событий
Основная терминология в алгебре событий
Случайная величина и вероятность события
Математическая статистика тесно связана с другой математической наукой – теорией вероятности и базируется на ее математическом аппарате.
Теория вероятности – это наука, которая изучает закономерности, порожденные случайными событиями.
Педагогические явления относятся к числу массовых: они охватывают большие совокупности людей, повторяются из года в год, совершаются непрерывно. Показатели (параметры, результаты) педагогического процесса имеют вероятностный характер: одно и то же педагогическое воздействие может приводить к различным следствиям (случайные события, случайным величинам). Тем не менее, при многократном воспроизведении условий определенные следствия появляются чаще других, – это и есть проявление так называемых статистических закономерностей (изучением которых занимаются теория вероятностей и математическая статистика).
Случайная величина (СВ) – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода. СВ реализуемая по ходу опыта и сама является случайной. Каждая СВ задает распределение вероятностей.
Основным свойством педагогических процессов, явлений является их вероятностный характер (при данных условиях они могут произойти, реализоваться, но могут и не произойти). Для таких явлений существенную роль играет понятие вероятности.
Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата. Вероятность невозможного события равна нулю, достоверного – единице (100%). Вероятность любого события лежит в пределах от 0 до 1 – в зависимости от того, насколько это событие случайно.
Если мы интересуемся событием A, то, скорее всего, можем наблюдать, фиксировать факты его появления. Потребность в понятии вероятности и ее вычисления возникнет, очевидно, только тогда, когда мы наблюдаем это событие не каждый раз, либо осознаем, что оно может произойти, а может не произойти. И в том и другом случае полезно использовать понятие частоты появления события f(A) – как отношения числа случаев его появления (благоприятных исходов) к общему числу наблюдений. Частота наступления случайного события зависит не только от степени случайности самого события, но и от числа (количества) наблюдений за этой СВ.
Существует два вида выборок СВ: зависимые и независимые. Если результаты измерения некоторого свойства у объектов первой выборки не оказывают влияния на результаты измерения этого свойства у объектов второй выборки, то такие выборки считаются независимыми. В тех случаях, когда результаты одной выборки влияют на результаты другой выборки, выборки считают зависимыми. Классический способ получения зависимых измерений – это двукратное измерение одного и того же свойства (или разных свойств) у членов одной и той же группы.
Событие А не зависит от события В, если вероятность события А не зависит от того произошло или нет событие В. События А и В независимы, если Р(АВ)=Р(А)Р(В). На практике независимость события устанавливается из условий опыта, интуиции исследователя и практики.
СВ бывает дискретной (мы можем пронумеровать ее возможные значения), например, выпадение игральной кости =4,6,2, и непрерывной (ее функция распределения F(x) – непрерывна), например, время службы лампочки.
Математическое ожидание – числовая характеристика СВ, приближенно равная среднему значению СВ:
M(x)=x1p1+x2p2+…+xnpn
Понятие вероятности
Теория вероятностей - это математическая теория, которая дает описание экспериментов со случайными исходами, обладающих свойством статистической устойчивости. Теория вероятностей строится как аксиоматическая теория, то есть в ее основу положена система аксиом. В свою очередь аксиомы сформулированы на основе экспериментальных данных, а именно на свойствах частоты и, в частности, на факте статистической устойчивости, состоящем в тенденции частоты 
появления события 
стать постоянной и равной некоторому числу 
при большом числе повторений 
эксперимента 
.
Таким образом, при построении теории необходимо ввести число называемое вероятностью события , что реализуется с помощью одной из аксиом, которая называется аксиомой существования вероятности. Далее необходимо рассмотреть основные свойства частот и выразить эти свойства как утверждения относительно свойств вероятностей. Эти утверждения вместе с постулатом существования вероятности образуют систему аксиом теории вероятностей.
Частоту можно рассматривать как результат измерения (оценивания) вероятности по экспериментальным данным. Таким образом, равенство 
означает, что при большом числе опытов 
, а ошибка 
имеет тенденцию снижаться с увеличением . Поскольку 
, то частота 
появления события в серии из опытов удовлетворяет условию 
. Аналогичному условию должна удовлетворять и вероятность: 
.
Рассмотрим значения вероятности на границах интервала 
. Пусть 
, тогда событие называется невозможным и обозначается символом 
. Для невозможного события его частота 
и имеет тенденцию приближаться к нулю с увеличением числа опытов. Если 
, то событие называется достоверным и обозначается символом 
. Частота достоверного события 
и с увеличением числа опытов имеет тенденцию приближаться к единице.
Алгебра событий
Рассмотрим основные операции над событиями и понятие алгебры событий. Пусть - некоторое событие.
1. Дополнением события называется событие 
, состоящее в том, что событие не произошло. Операциям над событиями можно давать простую геометрическую интерпретацию. Рассмотрим такую интерпретацию операции дополнения. Пусть эксперимент состоит в случайном бросании точки на плоскость, при этом множество условий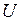 
таково, что исход каждого опыта – это попадание точки в область плоскости.
По определению – это событие, состоящее в том, что не произошло. Поэтому в данной интерпретации – это непопадание точки в область , то есть – попадание точки в заштрихованную область, рис.4.1.
2. Объединением (или суммой) двух событий и 
называется третье событие 
, состоящее в том, что произошло хотя бы одно из событий или . Для объединения будем использовать обозначение 
или 
. Признаком операции объединения двух событий может служить союз "или" между ними. Операции объединения, аналогично дополнению, можно дать геометрическую интерпретацию. Пусть – событие, состоящее в том, что случайно брошенная на плоскость точка попала в область, обозначенную также , рис. 4.2. Аналогично событие – это попадание точки в область . Операция объединения определяется для произвольного числа событий. Например, событие 
состоит в том, что происходит хотя бы одно из событий , …. Событие 
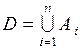состоит в том, что происходит хотя бы одно из событий 
… 
. Очевидно операция объединения коммутативна по определению: 
и ассоциативна, что также следует из определения: 
.
3. Пересечением (или произведением) двух событий и называется третье событие , состоящее в том, что произошли оба события и . Для обозначения операции пересечения будем использовать обозначения 
или 
. Операция пересечения, также как и операция объединения, определяется для произвольного числа событий. Например, событие 
состоит в том, что происходят все события 
Событие 
состоит втом, что происходят все события 
. По определению операция пересечения коммутативна, то есть выполняется условие: 
, а также ассоциативна:
.
Операции объединения 
и пересечения 
взаимно дистрибутивны. В частности, операция объединения дистрибутивна относительно пересечения:
.
Отметим, что если в для операции объединения используется знак "+", а для пересечения – отсутствие знака, то принимает хорошо знакомый вид: 
– закона дистрибутивности умножения относительно сложения в алгебре чисел. В отличие от этого закон дистрибутивности сложения относительно умножения не имеет аналога в алгебре чисел.
Рассмотренные операции над событиями носят алгебраический характер. Поэтому в теории вероятностей важное значение имеет алгебра событий, которая определяется следующим образом.
Система событий 
называется алгеброй событий, если для любой пары событий и из условий 
следует, что события , 
, 
, 
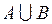содержатся в .
Говорят, что алгебра событий – это система событий, замкнутая относительно операций дополнения, пересечения и объединения.
