Завершение этапа крутого восхождения.

Основные свойства ортогонального планирования.

12.Основные свойства ротатабельного планирования.
Ротатабельность - способность матем. модели, полученной в рез-те ПФЭ и ДФЭ, предсказывать зн-ние пар-pa оптимизации с одинаковой точностью на равной расст. от центра эксперим. независимо от направления.

Свойства ротатабельности: 1)равенство дисперсий коэффициентов;

13.Движения по градиенту линейного уравнения регрессии (крутого восхождения).
Предположим, что после первого этапа решения задачи было получено линейное уравнение или линейная функция отклика: . Можно доказать, что движение из некоторой точки внутри изученной области в направлении наибольшей производной функции – кратчайший путь оптимума: , где dy, dx – частные производные функции отклика i,j,m – единичные векторы в направлении координатных осей факторного пространства. Очевидно, что dy, dx линейные функции по каждой из переменных равный соответствующему коэффициенту 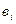: . Для осуществления движения по градиенту значения факторов по каждой из осей i,j и m необходимо изменять пропорционально величинам коэффициентов , b2….bk с учетом их знаков. Движение по градиенту обеспечивает наиболее быстрый путь к оптимуму, так как направление градиента представляет собой самого крутого склона, ведущего по данной точке к вершине. Движение по самому крутому склону – крутовосхождение, метод же – метод крутого восхождения. Обобщение на случай k факторов делается механически, так как 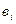рассчитаны не зависимо друг от друга. Определяют произведение соответствующих интервалов b1 на Δ , выбирают шаги в изменении каждого фактора пропорционально величине * Δ .Полученные т.о шаги последовательно прибавляют, или вычитают в зависимости от знака коэффициентов регрессии к основному уровню каждого фактора. Для качественных факторов, либо фиксируют лучший уровень, либо реализуют опыты поочередно для каждого уровня. Незначительные факторы стабилизируют на уровне в интервале и в дальнейшем движении по градиенту, эти факторы не участвуют. Если при крутом восхождении не возможно двигаться по какому-либо из факторов, его стабилизируют на достигнутом уровне, по остальным факторам, движение продолжают. Успех крутого восхождения очень сильно зависит от характера поверхности отклика.

 

Наиболее благоприятные движения по градиенту А, Б (меняется фактор-меняется и направление), В также. Г, ничего хорошего не даст, значения x разные, дают разные значения.

Либо план уже находится в области оптимума, либо были допущены грубые ошибки на этапе планирования эксперимента. Результат движения по градиенту во многом определяется соотношение численных значений коэффициентов регрессии. Наиболее оптимальное движение по градиенту, симметричной функции, т.е функции, величины коэффициентов которых различаются не существенно. Если функция резко несимметрична, движение по градиенту может выразиться в однофакторный эксперимент, когда в опытах будет изменяться один из факторов. Удачный выбор интервала варьирования может сделать симметричной, практически любую функцию.

14.21.Способы расчета коэффициентов регрессии при использовании ПФЭ и ДФЭ.
Полный: , где y- номер опыта; i- № фактора; - значение параметра оптимизации в опыте № N; - значение фактора № i в опыте № n. Таким образом для подсчета коэффициента к столбцу y надо приписать знаки соответственного столбца , сложить значения параметра оптимизации, а результат разделить на число опытов матрицы планирования N.

15.Способ определения доверительных интервалов коэффициентов регрессии.
Рассчитывается по формуле: , где t- критерий Стьюдента; N – число опытов матрицы планирования; - СКО в определении коэффициентов регрессии ()

16.Статистически значимые и статистически незначимые коэффициенты регрессии.
Коэффициент регрессии считается статистически значимым если его абсолютная величина ≥ доверительному интервалу |b_i|≥∆b_i; . Смысл неравенства – абсолютная величина коэффициента должна быть в t раз больше, чем ошибка в его определении.

17.Схема расчета дисперсии неадекватности.
Критерий Фишера: гипотеза об адекватности нашей модели чаще всего определяется по критерию Фишера:

f1,f2 - число степеней свободы - разность между числом опытов и числом констант, вычисляемых по результатам опытов, независимо друг от друга.S2неад - вычислена с f2, S2{y} - вычислена с f1. Выражение, которое написано в числителе, так называется - дисперсия неадекватности. Достаточная дисперсия, дисперсия адекватности:

YuрасчYuэксп - значения параметров оптимизации в опыте и рассчитанные оп уравнению регрессии и определяющиеся экспериментально. N-K =f2 - число степеней свободы при определении дисперсии неадекватности. N - количество экспериментов. К' - число коэффициентов регрессии, включая b0. Критерий Фишера представляет собой отношение дисперсии предсказания полученной модели к дисперсии опыта. Он показывает во сколько раз модель предсказывает хуже, чем опыт. Гипотеза об адекватности модели принимается в том случае, когда расчет значения критерия Фишера не превышает табличного для выбранного условия значимости Fрасч<=Fтабл. Формулы используются только в том случае, если отсутствует дублирование в матрице планирования. Если опыты дублируются равномерно, т.е опыты повторяются п раз. тогда расчет следующий:

,тогда дисперсия неадекватности При неравномерном дублировании нарушается ортогональность матрицы планирования и изменяются формулы для коэффициентов регрессии и дисперсии.

18.Способ проверки адекватности линейного уравнения с помощью критерия Стьюдента.
Коэф-т b₀ определяется по результатам полного и дробного факторного эксперимента и
является оценкой результата опыта на основном уровне, когда все факторы в кодовом
масштабе равны нулю.. Если выполнять опыт на основном уровне, то получим величину
параметра оптимизации на основном уровне у₀ Если разница (b₀- ) будет большой, то это означает, что линейным уравнением пользоваться нельзя. А значимость различия можно оценить с помощью критерия Стьюдента:

S{y}-среднеквадратическая ошибка опыта, которая определяется при f₁ степени свободы.

u - номер уровня, n - число параллельных опытов, - среднеарифметическое результатов опытов. Гипотеза об адекватности уравнения принимается в том случае когда

19.Общая схема планирования экспериментов для решения экстремальных задач.
Экстремальная задача - предполагает что параметр оптимизации связан с факторами тем или иным математическим выражением. Требуется так поставить эксперименты, чтобы при их минимальном количестве, варьируя значения независимых переменных, найти область оптимальных значений параметров, и, следовательно, построить математическую модель
А)выбрать параметры оптимизации у и влияющие факторы х₀, x1…x_k
Б)выбрать основной уровень xio и интервалы варьирования дельтах! влияющих факторов,
В)выбрать план эксперимента (полный или дробный факторный эксперимент)
Г)провести эксперименты
Д)на их основе составить модель (линейную, квадратичную)
Е)методом крутого восхождения найти оптимум.

20.Генерирующее соотношение и определяющий контраст.
Генерирующее соотношение показывает, с каким из эффектов смешан данный эффект. Пример X₁X₂=X₃ (1)-эффект 3 смешан с эффектами 1 и 2. Умножим (1) на Х₃,то Хз²=X₁X₂X₃ (X_i²=1)=> X₁X₂X₃=1. Символическое обозначение произведения столбцов равное (+1) или (-1) называют определяющим контрастом. С помощью него можно определить систему смешивания эффектов. Чтобы определить какой эффект смешан с данным, надо умножить обе части определяющего контраста на столбец, соответствующий данному эффекту: X₁=X₁² X₂ Х₃, X₁= X₂ Х₃, т.к. X₁²=1; X₃= X₁X₂

22.27.Линейная модель уравнения регрессии в матричной форме.
По результатам эксперимента необходимо определить коэффициент модели . Если искомые уравнения нелинейные, их всегда можно привести к линейным, заменив нелинейную составляющую новыми переменными. Коэффициенты регрессии чаще всего определяют по МНК.

Систему всех обозначений и вывод формул можно упростить, используя линейную алгебру , , х - матрица условий эксперимента.
K-количество факторов, n – число опытовB- Матрица неизвестных коэффициентов регрессии , Y – матрица результатов наблюдений ,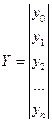

, - транспонированная матрица (строки заменены столбцами)

- система нормальных уравнений МНК записанных в матричной форме

Элементы матрицы B определяются из решения этой системы. Получим матрицу обратную

Для расчета коэффициентов регрессии, необходимо найти следующие матрицы .Матрица Х-ортогональная, так как для любых пар столбцов

23.Указать какая часть поверхности отклика называется почти стационарной.
Часть поверхности отклика вблизи экстремума называется почти стационарной областью, она обычно описывается при помощи нелинейных уравнений, чаще всего это полином второго порядка 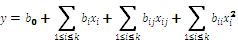,где к - число факторов

Для решения такой задачи, придется пользоваться планированием 2-го порядка.

24.Объяснить каким образом матрицу центрального композиционного планирования можно сделать ротатабельной.
Когда проводится эксперимент неизвестно, какое направление факторного пространства представляет больший интерес => необходимо получить одинаковое количество информации по разным направлениям, необходимо, чтобы информации была равномерно распределена по факторному пространству. Используется другой способ, позволяющий равномерно распределить информацию. Это достигается выбором определенного значения звездного плеча и числа опытов в центре эксперимента.
Условия ротатабельности формулируются: достигается инвариантность к вращению координат, позволяющая предсказать значения параметра оптимизации в различных точках факторного пространства с минимальными и равными на равном расстоянии от центра эксперимента дисперсиями; из условия ротатабельности величина звездного плеча определяется если в качестве ядра плана – ПФЭ. Если ядром плана служат дробные реплики, то .

 

25.Основные особенности этапа выбора факторов.
На первых этапах в программу исследования вносят все факторы. Часто выбранных факторов оказывается слишком много. В этом случае возникает задача выявления наиболее сильно влияющих факторов и их взаимодействий. Все способы выбора факторов при взаимодействии основаны на том, что они ранжируются. Все факторы, которые не включаются в начальные этапы стабилизируются на каком-то постоянном уровне.

26.Указать каким образом матрицу центрального композиционного планирования можно сделать ортогональной.
Одним из достоинств ортогонального планирования является возможность оценить коэффициенты регрессии независимо друг от друга , где N-число опытов, u- номер опыта, i, j = от 0 до x – число факторов. Это условие в общем случае для матрицы центрального композиционного плана не выполняется, так как в таблице сумма произведений не равна нулю. ;. Условия не выполняются, но можно добиться полной ортогональности данного планирования если преобразовать квадратичные переменные и специальным образом выбрать величину звездного плеча. С этой целью вместо вводят новые переменные . В результате этого соблюдаются условия ортогональности:
28.Рандомизация опытов во времени.
Для того, чтобы исключить влияние систематических ошибок, вызванных внешними условиями, рекомендуется опыты проводить в случайной последовательности (рандомизированно во времени). Если достаточно много опытов, то порядок их проведения можно установить по таблице случайных чисел. При проведении эксперимента необходимо учитывать ошибки самого опыта или дисперсию опыта.

29.Центральные композиционные планы.
при числе факторов не более 5! Предполагает реализацию ПФЭ, если к<5(число факторов) или ДФЭ, если к>5 Реализуем опыты ПФЭ или ДФЭ, а потом добавляем к этим опытам (ядру) некоторое количество специальным образом расположенных точек, такие планы носят название центральных. Для центральных планов все опыты располагаются симметрично вокруг центра. Данные планы являются центральными композиционными.

30.Описать способ установления шага в измерении факторов при движении по градиенту (крутом восхождении).
Выбирают шаги в изменении каждого фактора пропорционально величине * Δ .Полученные т.о шаги последовательно прибавляют, или вычитают в зависимости от знака коэффициентов регрессии к основному уровню каждого фактора. (b_i – значение коэффициента регрессии, ∆x_i – интервал варьирования)

Завершение этапа крутого восхождения.

32.Общее число опытов при центральном композиционном планировании.
Общее количество опытов N при k факторах в ОЦКП равно N = N₁+2k+ n₀.

Если k>5 ИЛИ k=5,то N₁= 2^k–p;

Если k<5,то N₁= 2^k.

N₁-число опытов ядра плана;

2k-кол-во звездных точек

n_o-число опытов в центре плана.