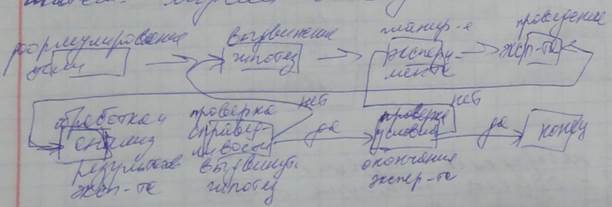
Выделение существенных факторов.
При исследовании сложных процессов, на которые воздействует большое число факторов, обычно заранее неизвестны, какие из этих факторов считать доминирующими.
Такие методы построения математических моделей, как регрессионный анализ, включают в себя проверку значимости коэффициентов регрессии при большом числе факторов неприемлемы (Почему? Требует большого числа опытов.).
Цель полученных методов: получение грубых оценок взаимодействия факторов при возможно меньших затратах (при минимизации числа опытов).
1. Дисперсионный анализ, в основу которого положено предположение о том, что существенность некоторого дискретного фактора характеризуется его вкладом в дисперсию входной величины (в курсе статистических методов).
2. Насыщенные дробные факторные планы основаны на предположении о наличие эффектов и, приводящие к оценке существенных факторов по их вкладу в математическое ожидание выходной величины.
3. Насыщенные экспериментальные планы Плакетте - Бермана, которые предполагают наличие только линейных эффектов.
4. Метод случайного баланса предполагает, что среди рассматриваемых факторов не все являются существенными, что позволяет применять сверхнасыщенное планирование, в котором число факторов больше числа опытов.
5. Опрос экспертов с целью ранжирования факторов по степени их влияния.
Введем понятие
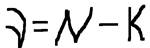
- число степеней свободы;
N – число опытов;
К – число искомых параметров.
Насыщенность плана:
Если > 0 и N>K, то есть число проведенных опытов превышает число оцениваемых параметров, то план называется насыщенным.
При = 0, N=K – насыщенный;
При <0, N<K – число оцениваемых параметров превышает число опытов – сверхнасыщенный.
Насыщенные дробные факторные планы.
Зависимость между целевой функцией и факторами, представляется в виде линейной модели:
y=b0+∑ni=1bixi
Допущения: доминирующими являются только линейные эффекты. Число опытов 1 на уровне +1;-1 = числу искомых параметров.
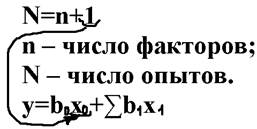
С помощью дробного насыщенного факторного плана
2k-m , где
2 – число уровней;
k – число факторов;
m – число взаимодействий, которые занимает фактор.
Можно исследовать фактор 2k-m факторов, т е 3,7, 15, 31, 63 и т д факторов (вместо k подставить цифры).
Оценка коэффициентов регрессии bi определяется независимо друг от друга и смещена с взаимодействиями, если таковые имеются. Значимость коэффициентов регрессии а => и факторов проверяется с помощью t критерия, доверительные границы для каждого коэффициента следующие:
bi - tSbi < βi < bi + tSbi
βi - искомое значение коэффициента регрессии;
bi - оценка коэффициента регрессии βi;
t – табличное значение критерия Стьюдента (знать уровень значимости – ошибка (примерно = 5%) + число степеней свободы).
Sbi - ошибка определения bi.
(Несколько раз определяем коэффициент bi, определяем разброс – эмпирически СКО).
Если попадает βi попадает в доверительный интервал для некоторого коэффициента регрессии, то соответствующий фактор признается несущественным.
Насыщенный эксперимент, планы Плакетте – Бермана.
Эти планы расширяют класс насыщенности ортогональности ортогональных планов эксперимента, за счет конструирования специальных матриц планов, число опытов в этих матрицах кратно 4.
N=4K с их помощью можно исследовать 4K-1 факторов, т е 3,7, 11, 15, 19, 23 и т д., т к эти планы ортогональны линейные эффекты факторов находятся независимо друг от друга.
Построение матриц.
Первые строки матриц плана, содержащие от 8 до 72 опытов приведены в справочнике. Факторы варьируются на уровнях +1;-1. Полные планы матриц конструируются следующим образом: исходя из заданной правой строки; 2ю и последующие строки получают путем сдвига всех элементов предыдущей строки на 1 позицию вправо/влево к перестановке последнего (первого) элемента на 1ю (последнюю) позицию. Этот процесс повторяется N-2 раз. Последняя строка планов состоит из элементов -1. Матрица плана имеет размерность N(N-1).
В качестве примера рассмотрим план для N=8.
| № | X1 | X2 | X3 | X4 | X5 | X6 | X7 |
| + | + | + | - | + | - | - | |
| + | + | - | + | - | - | + | |
| + | - | + | - | - | + | + | |
| - | + | - | - | + | + | + | |
| + | - | - | + | + | + | - | |
| - | - | + | + | + | - | + | |
| - | + | + | + | - | + | - | |
| - | - | - | - | - | - | - |
1я строка из справочника – сдвиг влево – последняя из «-».
Далее производится обработка результатов эксперимента, которая включает расчет эффектов отдельных факторов и проверку значимости коэффициентов регрессии.
Метод случайного баланса.
Если число факторов велико, целесообразно применять сверх насыщенные планы, что позволяет уменьшить число опытов. Этот метод позволяет выделять существенные факторы из множества самих факторов тех и их пар взаимодействия. Предполагает, что из всего множества факторов наибольшее их число оказывает влияние на целевую функцию.
Предполагается, что математическая модель объекта включает линейные эффекты и парные взаимодействия факторов. Задача состоит в таком изменении модели, чтобы она содержала лишь существенные факторы.
Целью экспериментов: в методе случайного баланса является упорядочение факторов по степени их влияния на целевую функцию и оценка коэффициента модели.
Построение плана эксперимента можно производить либо с применением случайных чисел для установления последовательности факторов столбца матрицы плана, либо путем случайного смешивания для дробных факторных планов.
Планы для изучения поверхности отклика.
В большинстве задач по изучению поверхности отклика вид зависимости между откликом и независимыми переменными неизвестен.
Анализ поверхности отклика – последовательная процедура. В начале исследования находимся в точке на поверхности отклика, далекая от оптимума.
Кривизна в системе невелика и приемлемая, оказывается модель 1го порядка, которая позволяет выйти в окрестность оптимума.
Когда область оптимума определена, целесообразно применить более сложную модель (поленом 2го порядка) и провести анализ для локализации оптимума.
Для выбора модели 1го порядка
y=b0+b1x1+b2x2+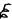 
существует единственный класс планов минимизирующий дисперсию коэффициентов регрессии bi.
Это ортогональные планы 1го порядка.
План типа 2k не позволяет оценить ошибку эксперимента. Необходимо проверить некоторые опыты.
Наиболее распространенным методом является дополнение плана несколькими наблюдателями в центре, т е введение в план типа 2k несколько центральных точек.
Другим ортогональным планом 1го порядка является СИМПЛЕКС, который представляет собой правильную фигуру с «k+1» вершиной в «k» измерениях.
При k=2 симплекс план – равносторонний
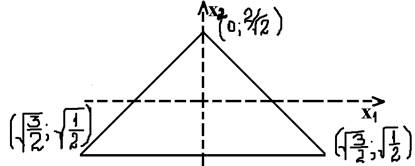
Симплексный план при k=2.
При k=3 – правильный тетраэдр.
План подбора модели 2го порядка.
Для подбора всех коэффициентов полиномов 2й степени план эксперимента должен содержать, по меньшей мере, 3 уровня каждого фактора.
y=b0+b1x1+b2x2+b12x1x2+b11x12+b22x22
Применение плана 3k связано с большим числом опытов. В результате исследований более рациональным является центральное экспозиционное планирование.
Центральные композиционные планы.
Этот план получают достройкой некоторого количества точек к «ядру» плана за который при числе факторов k<5 принимается ПФЭ 2k; k>5, то за ядро центра композиционного плана принимают полуреплику ПФЭ 2k.
Такой выбор ядра обусловлен тем, что от ядра плана требуется раздельная оценка всех линейных эффектов и эффекты взаимодействия.
Схема и матрица центрального композиционного плана для k=2.
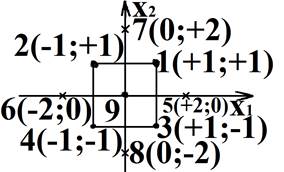
| № | x0 | x1 | x2 | x1x2 | x12 | x22 | y | |
| План типа 2k | + | + | + | + | + | + | y1 | |
| + | - | + | - | + | + | y2 | ||
| + | + | - | - | + | + | y3 | ||
| + | - | - | + | + | + | y4 | ||
| «Звезд ные точки» | + | +2 | α2 | y5 | ||||
| + | -2 | α2 | y6 | |||||
| + | α2 | y7 | ||||||
| + | α2 | y8 | ||||||
| Нулевая точка | + | y9 |
Из схемы плана ПФЭ 22 (точки 1,2,3,4) добавляется некоторое число n0 опытов в центре плана (точка 9) и 4 «звездных» точек (точки 3-8) с координатами 5(+2;0); 6(-2;0).
Чтобы получить центральный план композиционный план 2го порядка для k=3 к ПФЭ 23 добавляют в звездных точках и число. По точке в центре плана.
Ортогональные планы второго порядка.
«+» ортогональных планов: малый объем вычислений; можно показать, что в матрице центрального композиционного плана не все столбцы ортогональны.
Для ортогональности матрицы необходимо преобразовать ее столбцы.
Значение звездного плеча α для различного числа факторов:
| Число независимых переменных | «Ядро» плана | Число дополнительных опытов | Величина α |
| 22 | |||
| 23 | 1,215 | ||
| 24 | 1,414 | ||
| 25-1 | 1,547 |
При α=1 новые переменные x1`и x2`:
x1`= x12-2/3;
x2`=x22 -2/3.
Матрицы ортогонального центрального композиционного плана 2го порядка 2х факторов.
| № | x0 | x1 | x2 | x1x2 | x12-2/3 | x22-2/3 | y | |
| План типа 2k | + | + | + | + | +1/3 | +1/3 | y1 | |
| + | - | - | - | +1/3 | +1/3 | y2 | ||
| + | + | - | - | +1/3 | +1/3 | y3 | ||
| + | - | + | + | +1/3 | +1/3 | y4 | ||
| «Звезд ные точки» | + | + | +1/3 | -2/3 | y5 | |||
| + | - | +1/3 | -2/3 | y6 | ||||
| + | + | -2/3 | +1/3 | y7 | ||||
| + | - | -2/3 | +1/3 | y8 | ||||
| Нулевая точка | + | -2/3 | -2/3 | y9 |
Т к матрица ортогональная, то коэффициенты регрессии определяются независимо друг от друга по формуле:
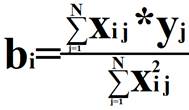
i – номер столбца;
j – номер опыта (строки).
Рототабельное планирование 2го порядка.
Информация о поверхности отклика, получена при ортогональном планировании 2го порядка, различна в разных направлениях.
Начиная эксперимент мы не знаем какое направление будет представлять больший интерес. Разумным является использование центральных композиционных планов, отвечающих требованиям рототабельности, т е план, позволяющий получить модель способную предсказать значение параметра оптимизации с одинаковой точностью, независимо от направления на равных расстояниях от центра плана.
Рототабельность композиционного плана достигается выбором величины звездного плеча α.
Для ядра содержащего полный факторный эксперимент α=2k/4, для ядра содержащего дробную реплику α=2(k-m)/4.
Для рототабельного планирования 2го порядка важное значение имеет выбор числа опытов в центре плана.
Данные для построения рототабельного центрального композиционного плана 2го порядка:
| Число факторов | «Ядро» плана | Число точек ядра nя | Число звездных точек n2 | Число нулевых точек n0 | Величина звездной реплики планирования α | Общее число опытов № |
| 22 | 1,414 | |||||
| 23 | 1,682 | |||||
| 24 | ||||||
| 25 | 2,378 | |||||
| 25-1 |
Матрица рототабельного центрального композиционного плана 2го порядка для 2х факторов.
| № | x0 | x1 | x2 | x1x2 | x12 | x22 | y |
| + | + | + | + | + | + | y1 | |
| + | - | + | - | + | + | y2 | |
| + | + | - | - | + | + | y3 | |
| + | - | - | + | y4 | |||
| + | +1,414 | y5 | |||||
| + | -1,414 | y6 | |||||
| + | +1,414 | y7 | |||||
| + | -1,414 | y8 | |||||
| + | y9 | ||||||
| + | y10 | ||||||
| + | y11 | ||||||
| + | y12 | ||||||
| + | y13 |
Матрица рототабельного планирования 2го порядка не ортогональны => объем вычислений при определении коэффициента регрессии велик.
