
где j – угол поворота; w z – проекция угловой скорости на ось вращения.
Если w z=const, то j=w z t.
Если угловое ускорение e =const, то  где w 0 – начальная угловая скорость. Угловая скорость при таком вращении w=w 0+ et.
где w 0 – начальная угловая скорость. Угловая скорость при таком вращении w=w 0+ et.
Ускорение в плоском криволинейном движении

Рис. 1.1
 ,
,  или
или  ,
,
где 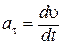 – скорость изменения модуля скорости (см. рис. 1.1).
– скорость изменения модуля скорости (см. рис. 1.1).
Сопоставление уравнений поступательного и вращательного движения показано в табл. 1.
Таблица 1
| Поступательное движение | Вращательное движение |
| S, x | φ |
| υ | ω |
| aτ | ε |

| 
|
| u x= u 0x+ a x t | w z= w 0z+ e z t |

| 
|
| 2 a x s x= u x2– u 0x2 | 2 e z j z= w z2– w 0z2 |
СПРАВОЧНЫЙ МАТЕРИАЛ
Заряд электрона e=1,6×10-19 Кл
Масса электрона m=9,1×10-31 кг
Ускорение свободного падения g=9,8 м/с2
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что изучает механика как один из разделов физики? Каково содержание: а) ньютоновской; б) релятивистской; в) квантовой механики?
2. Почему при изучении реальных физических явлений и объектов приходится использовать модельные представления и абстрагированные понятия? Дайте определение: а) материальной точке (частице); б) системе материальных точек; в) абсолютно твердому телу.
3. Каково содержание понятий пространства и времени в классической механике? Что означают понятия "однородность и изотропность пространства'', "однородность времени"?
4. Какие существуют способы описания движения материальной точки? Что представляет собой система отсчета, система координат? Что называется радиус-вектором  ?
?
5. Покажите, что задание кинематического закона движения в координатной форме х=х (t), у=у (t), z=z (t) эквивалентно заданию его в векторной форме  , где х, у, z – декартовы координаты положения материальной точки,
, где х, у, z – декартовы координаты положения материальной точки,  – ее радиус-вектор. Каковы преимущества векторного описания движения?
– ее радиус-вектор. Каковы преимущества векторного описания движения?
6. Дайте определение кинематических величин: а) перемещения  ; б) скорости
; б) скорости  ; в) ускорения
; в) ускорения  . В каких единицах измеряются эти величины? Как ориентированы векторы скорости и ускорения относительно траектории и друг друга?
. В каких единицах измеряются эти величины? Как ориентированы векторы скорости и ускорения относительно траектории и друг друга?
7. Частица движется по закону  где u 0 и g – известные постоянные;
где u 0 и g – известные постоянные;  – орт координатной оси z. Найдите скорость
– орт координатной оси z. Найдите скорость  частицы и ее ускорение
частицы и ее ускорение  , а также их проекции
, а также их проекции  и
и  как функции времени.
как функции времени.
8. Ускорение движущейся частицы  где A – известная постоянная;
где A – известная постоянная;  – орт координатной оси х. В момент времени t =0 х=x 0 и ux=u 0, где х 0 и u 0 – известные постоянные (начальные условия). Найдите проекцию скорости
– орт координатной оси х. В момент времени t =0 х=x 0 и ux=u 0, где х 0 и u 0 – известные постоянные (начальные условия). Найдите проекцию скорости  и координату x как функции времени.
и координату x как функции времени.
9. Какое движение абсолютно твердого тела называется: а) поступательным; б) вращательным? Приведите примеры таких движений.
10. Что называется тангенциальным аt и нормальным а n ускорениями? Чему они равны? От чего зависит угол между векторами скорости  и полного ускорения
и полного ускорения  движущейся материальной точки?
движущейся материальной точки?
11. Какие векторы называют аксиальными? Дайте определение: а) угла поворота  твердого тела; б) угловой скорости
твердого тела; б) угловой скорости  ; в) углового ускорения
; в) углового ускорения  относительно неподвижной в пространстве оси вращения. В каких единицах измеряются эти величины?
относительно неподвижной в пространстве оси вращения. В каких единицах измеряются эти величины?
12. Колесо вращается вокруг неподвижной оси, проходящей через его центр масс. Обладает ли любая точка на ободе тангенциальным и нормальным ускорениями, если вращение происходит: а) с постоянной угловой скоростью; б) с постоянным угловым ускорением? Изменяются ли при этом модули этих величин?
ЗАДАЧИ ГРУППЫ А
1.(1.25) Зависимость пройденного телом пути s от времени t дается уравнением s=A+Bt+Ct 2+ Dt 3, где С =0,14 м·с-2 и D =0,01 м·с-3. Через какое время t после начала движения тело будет иметь ускорение a =1 м·с-2? Найти среднее ускорение < a > тела за этот промежуток времени.
Ответ: t =12 c, < a >=0,64 м·с-2.
2.(1.27) Камень, брошенный горизонтально, упал на землю через время t =0,5 с на расстоянии l =5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью u x он брошен? С какой скоростью u он упадет на землю? Какой угол j составит вектор скорости камня с горизонтом в точке его падения на землю.
Ответ: h =1,22 м; u x=10 м·с-1; u =11,1 м·с-1; j =26°12´.
3.(1.30) Камень брошен горизонтально со скоростью u 0=15 м·с-1. Найти нормальное а n и тангенциальное а t ускорения камня через время t =1 с после начала движения.
Ответ: а t=5,4 м·с-2; а n=8,2 м·с-2.
4.(1.31) Камень брошен горизонтально со скоростью u 0=10 м·с-1. Найти радиус кривизны R траектории камня через время t =3 с после начала движения.
Ответ: R =305 м.
5.(1.39) С башни высотой h 0=25 м брошен камень со скоростью u 0=15 м·с-1 под углом a =30° к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью u он упадет на землю? Какой угол j составит траектория движения камня с горизонтом в точке его падения на землю?
Ответ: t =3,16 c; l =41,1 м; u =26,7 м·с-1; j =61°.
6.(1.49) Вентилятор вращается с частотой n =900 об·мин-1. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N =75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
Ответ: t =10 c.
7.(1.52) Точка движется по окружности радиусом R =20 см с постоянным тангенциальным ускорением а t. Найти тангенциальное ускорение а t точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки u=79,2 см·с-1.
Ответ: а t=0,1 м·с-2.
8.(1.55) Колесо радиусом R =10 см вращается с угловым ускорением e =3,14 рад·с-2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость w; б) линейную скорость u; в) тангенциальное ускорение а t; г) нормальное ускорение а n; д) полное ускорение а; е) угол a, составляемый вектором полного ускорения с радиусом колеса.
Ответ: а) w =3,14 рад·с-1; б) u =0,314 м·с-1; в) a t=0,314 м·с-2; г) a n=0,986 м·с-2; д) a =1,03 м·с-2; е) a =17°46´.
9.(1.57) Точка движется по окружности так, что зависимость пути от времени дается уравнением s=A–Bt+Ct 2, где В= 2 м·с-1 и С =1 м·с-2. Найти линейную скорость u точки, ее тангенциальное а t, нормальное а n и полное а ускорения через время t =3 с после начала движения, если известно, что при t¢ =2 с нормальное ускорение точки а ¢n=0,5 м·с-2.
Ответ: u =4 м·с-1; a t=2 м·с-2; a n=2 м·с-2; a =2,83 м·с-2.
10.(1.64) Во сколько раз нормальное ускорение а n точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а t для того момента, когда вектор полного ускорения точки составляет угол a =300 с вектором ее линейной скорости?
Ответ: a n/ a t=0,58.
РЕШЕНИЕ ЗАДАЧ ГРУППЫ А
1.(1.25) Зависимость пройденного пути s от времени t дается уравнением  , где
, где  м·c-2,
м·c-2,  м·c-3. Через какое время t после начала движения тело будет иметь ускорение
м·c-3. Через какое время t после начала движения тело будет иметь ускорение 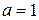 м·c-2? Найти среднее ускорение
м·c-2? Найти среднее ускорение  тела за этот промежуток времени.
тела за этот промежуток времени.
 м·c-2 м·c-2
 м·c-3
а =1 м·c-2 м·c-3
а =1 м·c-2
 =? =?
| Решение. 
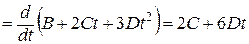 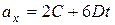 . .
|
 =12 с.
=12 с.  ,
,

 .
.
 =
=  м·c-2.
м·c-2.
Ответ: t =12 c, < a >=0,64 м·с-2.
2.(1.27) Камень, брошенный горизонтально, упал на землю через время t= 0,5 с на расстоянии l =5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью 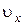 он брошен? С какой скоростью
он брошен? С какой скоростью  он упадет на землю? Какой угол φ составит вектор скорости камня с горизонтом в точке его падения на землю?
он упадет на землю? Какой угол φ составит вектор скорости камня с горизонтом в точке его падения на землю?
| t= 0,5 с l =5 м | 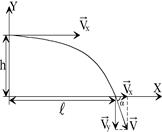
| Решение. Если пренебречь силой сопротивления воздуха, то вдоль оси OY камень движется равноускоренно без начальной скорости, а вдоль оси OX – равномерно.
 (1), а координата (1), а координата  – по закону – по закону  (2). При (2). При   , ,
|
h=?
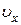 =? =?
 =?
φ=? =?
φ=?
|
 =0. Из (1)
=0. Из (1) 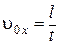 .
.  .
.  ,
,  ,
,  .
.  .
.  =10 м·с-1,
=10 м·с-1,  =11,1 м·с-1,
=11,1 м·с-1,  =0,49,
=0,49, 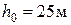 .
.
Ответ: h =1,22 м; u x=10 м·с-1; u =11,1 м·с-1; j =26°12´.
3.(1.30) Камень брошен горизонтально со скоростью  м·с-1. Найти нормальное
м·с-1. Найти нормальное  и тангенциальное
и тангенциальное  ускорения камня через время t= 1 c после начала движения.
ускорения камня через время t= 1 c после начала движения.
 м·с-1
t= 1 c м·с-1
t= 1 c
| 
| Решение.Если пренебречь силой сопротивления воздуха, то камень движется вдоль оси OX с ускорением  , а вдоль оси OY равномерно , а вдоль оси OY равномерно  . Полное ускорение камня . Полное ускорение камня  все время направлено вертикально вниз и равно ускорению все время направлено вертикально вниз и равно ускорению
|
 =? =?
 =? =?
|
свободного падения 
 ,
,  . Из рисунка имеем:
. Из рисунка имеем: 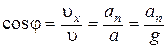 ;
;  . Отсюда
. Отсюда  ;
;  .
.  =8,2 м·с-2;
=8,2 м·с-2;
 =5,4 м·с-2.
=5,4 м·с-2.
Ответ: а n=8,2 м·с-2; а t=5,4 м·с-2.
4.(1.31) Камень брошен горизонтально со скоростью 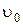 =10 м·с-1. Найти радиус кривизны R траектории камня через время t= 3 с после начала движения.
=10 м·с-1. Найти радиус кривизны R траектории камня через время t= 3 с после начала движения.
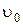 =10 м·с-1
t= 3 с
R=? =10 м·с-1
t= 3 с
R=?
| 
| Решение.  , ,  = g = g   , ,  , ,  . . 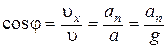 , ,
|
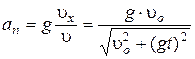 ;
;  .
.  =305 м.
=305 м.
Ответ: R =305 м.
5.(1.39) С башни высотой  =25 м брошен камень со скоростью υ0=15 м·с-1 под углом α=30º к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью υ он упадет на землю? Какой угол φ составит траектория движения камня с горизонтом в точке его падения на землю?
=25 м брошен камень со скоростью υ0=15 м·с-1 под углом α=30º к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью υ он упадет на землю? Какой угол φ составит траектория движения камня с горизонтом в точке его падения на землю?
 =25 м =25 м
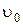 =15 м·с-1
α =30º =15 м·с-1
α =30º
| 
| Решение.  ; y =0; ; y =0;  ; ;
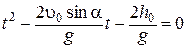 . .
|
t =?
l =?
 =?
φ=? =?
φ=?
|
 ;
;
 =3,15 c
=3,15 c
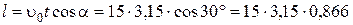 =40,9 м;
=40,9 м;
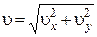 ;
;  ;
;

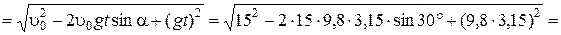
=  26,7 м·с-1;
26,7 м·с-1;  =0,487;
=0,487;
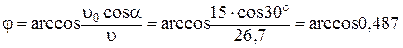 =60,9º
=60,9º
Ответ: t =3,16 c; l =40,9 м; u =26,7 м·с-1; j =61°.
6.(1.49) Вентилятор вращается с частотой n =900 об·мин-1. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N =75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
| n =900 об·мин-1 N =75 об ε=const ω=0 t=? | Решение.  , ,  , ,  ; ;  ; ;
 ; ;  ; ;  ; ;  ; ;  ; ;
 ; ;  ; ;  =10 c. =10 c.
|
Ответ: t =10 c.
7.(1.52) Точка движется по окружности радиусом R =20 см с постоянным тангенциальным ускорением а t. Найти тангенциальное ускорение а t точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки u=79,2 см·с-1.
| R =20 см а t=const N =5 u=79,2 см·с-1 а t=? | Решение.  ; ;  ; S =2π RN; ; S =2π RN;
 =0,05 м·с-2. =0,05 м·с-2.
|
2 способ
 ,
,  .
.  ,
, 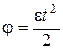 ,
,  .
.  ,
,  .
. 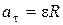 ,
,  .
.  =0,05 м·с-2.
=0,05 м·с-2.
Ответ: аt=0,05 м·с-2.
8.(1.55) Колесо радиусом R =10 см вращается с угловым ускорением e =3,14 рад·с-2. Найти для точек на ободе колеса к концу первой секунды после начала движения: угловую скорость w; линейную скорость u; тангенциальное ускорение а t; нормальное ускорение а n; полное ускорение а; угол a, составляемый вектором полного ускорения с радиусом колеса.
| R =10 см e =3,14 рад·с-2 t= 1 c w =? u =? а t=? а n=? а =? a=? | 
| Решение.  ; ;  ; ;
 =3,14 рад·с-1; =3,14 рад·с-1;
 =0,314 м с-1; =0,314 м с-1;
 =0,314 м с-2; =0,314 м с-2;
 =
=0,986 м·с-2; =
=0,986 м·с-2;
|
 =1,03 м·с-2;
=1,03 м·с-2;
 =0,303;
=0,303;
a =arcsin 0,303=17,67º.
Ответ: w =3,14 рад·с-1; u =0,314 м·с-1; a t=0,314 м·с-2; a n=0,986 с-2; a =1,03 м·с-2; a =17,67º.
9.(1.57) Точка движется по окружности так, что зависимость пути от времени дается уравнением s=A–Bt+Ct 2, где В= 2 м·с-1 и С =1 м·с-2. Найти линейную скорость u точки, ее тангенциальное а t, нормальное а n и полное а ускорения через время t =3 с после начала движения, если известно, что при t¢ =2 с нормальное ускорение точки а ¢n=0,5 м·с-2.
| В= 2 м·с-1 С =1 м·с-2 t =3 с t¢ =2 с а ¢n=0,5 м·с-2 u=? а t=? а n=? а =? | Решение.  ; ;  =
= 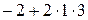 =4 м·с-1; =4 м·с-1;  ; ;
  =2 м·с-2; =2 м·с-2; 
|
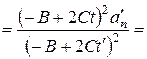
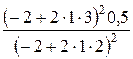 =2 м·с-2;
=2 м·с-2; 
 =2,83 м·с-2.
=2,83 м·с-2.
Ответ: u =4 м·с-1; a t=2 м·с-2; a n=2 м·с-2; a =2,83 м·с-2.
10.(1.64) Во сколько раз нормальное ускорение а n точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а t для того момента, когда вектор полного ускорения точки составляет угол a =30º с вектором ее линейной скорости?
| a =30 º | 
| Решение. 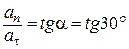 =0,58. =0,58.
|
 =? =?
|
Ответ:  =0,58.
=0,58.
ЗАДАЧИ ГРУППЫ Б
1. По прямой линии движутся две материальные точки согласно уравнениям: x 1= А 1+ В 1 t + C 1 t 2 и x 2= А 2+ В 2 t + С 2 t 2, где А 1=5 м, В 1=1 м·с-1, С 1=2 м·с-2, А 2=–6 м, В 2=4 м·с-1, С 2=0,8 м·с-2. В какой момент времени t скорости этих точек будут одинаковы? Найти скорости u1, u2 и ускорения a 1, a 2 этих точек в момент времени t 1=1 c.
Ответ: t =1,25 c; u1=5 м·с-1; u2=5,6 м·с-1; а 1=4 м·с-2; а 2=1,6 м·с-2.
2. Движение материальной точки задано уравнением x = Аt+Bt 2, где А =4 м·с-1, В =–0,05 м·с-2. Определить момент времени t, в который скорость точки u=0. Найти координату x и ускорение точки a в этот момент.
Ответ: t =40 c; x =80 м; а =–0,1 м·с-2.
3. Точка движется по окружности радиусом R =2 м. Уравнение движения точки j=Аt+Bt 3, где А =1 с-1, В =0,4 с-3. Определить тангенциальное a t, нормальное a n и полное a ускорения точки в момент времени t =2 с.
Ответ: а t=9,6 м·с-2; а n=67,3 м·с-2; а =68,0 м·с-2.
4. Колесо радиусом R =0,2 м вращается так, что зависимость от времени линейной скорости точек, лежащих на ободе колеса, задается уравнением u=At+Bt 2, где А =0,06 м·с-2, В =0,02 м·с-3. Найти угол a, который составляет вектор полного ускорения с радиусом колеса в моменты времени t 1=1 с, t 2=2 с после начала движения.
Ответ: a1=72,2°; a2=35°.
5. На вал радиусом R =10 см намотана нить, к концу которой привязана гиря. Двигаясь равноускоренно, гиря за t =20 с от начала движения опустилась на h =2 м. Найти угловую скорость и угловое ускорение вала для этого момента времени.
Ответ:  ;
;  .
.
6. При выстреле пуля вылетела со скоростью u0=200 м·с-1 под углом a=60° к горизонту. Определить наибольшую высоту подъема h, дальность полета S и радиус кривизны R траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.
Ответ: h =1530 м; S =3530 м; R =1020 м.
7. Тело брошено со скоростью u0=20 м·с-1 под углом a=30° к горизонту. Пренебрегая сопротивлением воздуха, найти скорость u тела, а также его нормальное a n и тангенциальное a t ускорения через t =1,5 с после начала движения. На какое расстояние x переместится за это время тело по горизонтали и на какой высоте y оно окажется?
Ответ: u=17,9 м·с-1; a n=9,72 м·с-2; a t=2,67 м·с-2; x =26 м; y =4 м.
8. Электроны, обладающие кинетической энергией Е к=1,6 кэВ, влетают посередине между пластинами плоского конденсатора параллельно им. Какое минимальное напряжение U m необходимо подвести к пластинам, чтобы электроны не вышли за пределы пластин? Длина пластин l =2 см, расстояние между ними d =1 см (1 кэВ=1,610-16 Дж).
Ответ: U m=800 В.
9. Электрон влетает в плоский конденсатор со скоростью u0=107 м·с-1, направленной параллельно пластинам. В момент вылета из конденсатора направление скорости электрона составляло угол a=35° с первоначальным направлением. Определить разность потенциалов между пластинами, если длина пластин l =10 см, а расстояние между ними d =2 см.
Ответ: U =79,6 В.
10. Определить величину отклонения луча y на экране осциллографа, если напряжение на отклоняющих пластинах U =150 В, их длина l 1=4 см, а расстояние между пластинами d =1 см. Расстояние от экрана до ближайшего края отклоняющих пластин l 2=15 см. Электроны ускоряются напряжением U 0=103 В.
Ответ: y=51×10-3 м.






