С учетом линейности задачи и принципа суперпозиции выражения для линейных деформаций очевидны
, (10)
, (11)
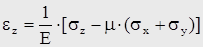. (12)
При рассмотрении кручения получена связь угловых деформаций и касательных напряжений. В обобщенном виде это
, (13) 
, (14) . (15)
Полная модель. Граничные условия
Среди 15-ти разрешающих уравнений девять дифференциальных в частных производных. Для замыкания задачи необходимо сформулировать граничные условия.
Границей тела является его поверхность 
. Во всех ее точках необходимо указать условия закрепления, которые могут быть силовыми, кинематическими или смешанными.
Первые имеют место, если в точке известны внешние поверхностные силы. Вторые – когда известны перемещения. Третьи – если известна зависимость между силами и перемещениями.
Рассмотрим более подробно силовые граничные условия, которые формулируются относительно сложно.
Напряжения на площадке, совпадающей с поверхностью, есть внешние силы, т.е. 
.
,
,
.
Этим уравнениям должны удовлетворять искомые функции напряжений в точках поверхности.
Кинематические условия есть ограничения на перемещения точек поверхности. В неподвижной точке, например, 
.
Смешанные условия, например, на упругом основании в плоскости xoz,
.
Методы решения задачи
Аналитическое решение в общем случае неизвестно.
Доказана теорема единственности: если найдено решение, удовлетворяющее 15-ти уравнениям и граничным условиям, то оно единственно.
Рассмотрим методы решения в частных случаях и общий подход к численному решению.
· Прямой метод
Метод возможен только в задачах, сводящихся к системе обыкновенных дифференциальных уравнений. Это, в основном, осесимметричные задачи с переводом в цилиндрические координаты. Примеры: задача Ламе, задача о действии сосредоточенной силы на бесконечное полупространство (из которой Герц построил решение контактной задачи), некоторые плоские задачи, в которых удается разделить переменные по методу Фурье.
· Обратный метод
Предполагаются: некоторая система искомых функций, заведомо удовлетворяющая 15-ти уравнениями, форма тела. Решается вопрос: как должно быть нагружено тело, чтобы удовлетворить граничным условиям.
Этим способом удалось решить несколько задач, имеющих практическое значение. Например: задача Фламмана о диске, сжатом по диаметру сосредоточенными силами, задача о плоском клине (положена в основу расчета режущего инструмента), и д.р. Конечно решать практические задачи этим методом не удается. Но он положен в основу многих численных методов. Рассмотрим пример, иллюстрирующий сущность метода.
Пусть тело нагружено так, что отсутствуют касательные напряжения, а нормальные равны σ. Граничные условия только силовые. Объемные силы отсутствуют. Что за тело и как нагружено?
Из уравнений равновесия получаем σ=const, т.е. в том числе и на границе тела. Угловые деформации раны нулю, линейные равны между собой
.
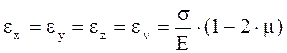Формулы Коши приводят к равенству производных от перемещений по осям
,
и, вследствие отсутствия кинематических и смешанных граничных условий, других ограничений на перемещения нет. Граничные условия требуют 
,
и, тело нагружено равномерным давлением, форма тела любая.
Одновременно очевидно 
, так как знак деформации должен совпадать со знаком напряжения.
· Полуобратный метод (Сен-Венана)
Часть свойств искомых функций и характера нагружения предполагается. Остальные выбираются так, чтобы удовлетворить 15-ти уравнениями и граничным условиям.
Рассмотрим метод на примере задачи о сжатии призмы по торцам. задача имеет непосредственное отношение к технической теории стержней, используемой в сопротивлении материалов.
Призма нагружена только по нормали к торцам (
), никак не закреплена, объемные силы отсутствуют. Ось z совпадает с осью призмы. Оси x и y- главные.
Силовые граничные условия:
- на боковой поверхности 
, 
, 
;
- на торцовой поверхности 
, 
,
. (16)
«Обратная» сторона метода состоит в предположении, что 
,
чем автоматически удовлетворяются пять граничных условий. Шестое условие – закон распределение нагрузок по торцу, выясняется в ходе анализа основной системы уравнений, которая принятым предположением существенно упрощается. В этом – «прямая» сторона метода.
Уравнения равновесия дают
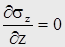, (3*,12*)
т.е. нормальные напряжения не зависят от z.
Геометрические соотношения соединим с законом Гука. Имеем
, (4*,5*,10*,11*) 
, (6*,9*)
,(7*,13*). 
, (8*,14*)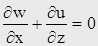 
, (9*,15*)
Дальнейшие действия называю математическим анализом.
Из (4*…), (3*…) получаем 
, а из (7*…), (8*…), (9*…) - 
. Соответственно 
, 
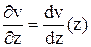и (8*…) и (9*…) удовлетворяет
. (17)
Подставляя результат анализа в (6*…) приходим к той же формуле для нормальных напряжений в стержне, что и раньше. Таким образом, гипотеза плоских сечений справедлива по всей длине призмы, если нагрузка на торце распределена по линейному закон у (см. (16)). Во всех других случаях она справедлива приближенно.
· Численные методы
Практически применяются два метода: метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Рассмотрим идеологию этих методов.
Полная система уравнений сводится к трем неизвестным функциям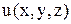 
, 
, 
- трем уравнениям Ламе – уравнениям равновесия, выраженным через перемещения. Если найти эти функции, то подстановкой в уравнения Коши получаем деформации, а, затем, подстановкой в уравнения закона Гука – напряжения. И, задача решена!!! Именно в этом и состоит принцип численного решения.
v В МКР тело разбивают сеткой на узлы, перемещения в которых считаются неизвестными. Частные производные вычисляются через перемещения данного узла и соседних узлов по определению производной. Полученные линейные зависимости подставляются в уравнения Ламе. В линейной постановке они также линейны относительно перемещений узлов. В крайних узлах формируются граничные условия. В итоге получаем большую систему линейных уравнений для перемещений узлов, которая решается ЭВМ численно по известным алгоритмам. Затем, зная перемещения узлов и их производные, находят напряжения в каждой точке.
Точность решения задачи зависит от размеров сетки и точности представления чисел в ЭВМ. Основной недостаток метода в сложности формулирования граничных условий конкретной задачи.
Сложность расчетов многократно увеличивается в случае нелинейной постановки, так как приходиться решать большую систему нелинейных алгебраических уравнений. Поэтому метод неидеальностей для определения критических нагрузок практически не применяется.
Задача в смысле Эйлера решается по следующему алгоритму.
Предполагаемую критическую нагрузку умножают на некоторый коэффициент, меняя который добиваются равенства нулю определителя линейной системы. Значение нагрузки, умноженное на соответствующее значение коэффициента, и есть критическая сила. Продолжая расчеты можно найти требуемое количество критических сил и форм потери устойчивости.
v В МКЭ тело разбивают на конечные элементы, например кубы, многогранники и т.д. Общие вершины элементов являются узлами.
Алгоритм получения разрешающей системы линейных алгебраических уравнений для перемещений в узлах иной. Здесь на базе теоремы Лагранжа-Дирихле для выбранных элементов находится матрица жесткостей, т.е. математическая связь сил и перемещений в узлах. Затем для каждого узла составляется система уравнений равновесия, в том числе и для граничных узлов, ГД прикладываются внешние силы или ограничиваются перемещения. Поэтому запись граничных условий проще и легко автоматизируется.
В остальном идеология метода идентична МКР. Недостатки и сложности также аналогичны. В некоторых случаях удачный выбор типа элемента позволяет понизить порядок разрешающей системы.
