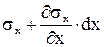Полная математическая модель упругого деформируемого тела
До сих пор мы рассматривали задачи в постановке сопротивления материалов. При этом стремились строить модели в виде, доступном для аналитического решения или численного интегрирования без применения специальных программных пакетов. Фактически мы рассматривали только те задачи, описание которых сводилось к системе обыкновенных дифференциальных уравнений. Схематизировались объекты и свойства материалов, что приводило к приближенным результатам. При этом в реальных расчетах приходилось брать существенные запасы прочности.
Некоторые задачи вообще не решаются в такой постановке. В других приходится вводить так называемые коэффициенты концентрации напряжений, определяемые экспериментально, и учитывающие особенности НДС в особых точках или зонах. Развитие вычислительной техники и численных методов позволяет решать задачу при гораздо меньшей схематизации. Мы в нашем курсе ограничимся только следующей схематизацией: закон Гука и малые перемещения и деформации. Такая постановка приводит к моделям, доступным для численного (а, иногда, и аналитического) решения.
Постановка задачи и параметры математической модели
Решаем задачу в декартовых координатах относительно неподвижной исходной правой системы осей xyz.. Некоторые параметры задачи и уравнения связи уже рассматривались:
- неизвестные функции от координат –
параметры НС в точке с координатами x, y, z;
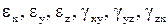- неизвестные функции от координат –
параметры ДС в точке с координатами x, y, z;
- неизвестные функции от координат –
перемещения точки с координатами x, y, z;
- известные функции от координат –
проекции давления поверхностных сил на
поверхность тела в точке точки с координатами x, y, z;
- известные функции от координат –
проекции объемных сил в точке точки
с координатами x, y, z;
- известная функция от координат,
описывающая поверхность тела до нагружения.
Для нахождения 15-ти неизвестных функций необходимо 15 уравнений. Получим их.
Уравнения равновесия в напряжениях
В точке можно составить три уравнения равновесия равенство нулю суммы сил в проекции на координатные оси. Например, на ось х:
|
|
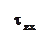
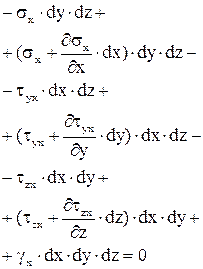
После преобразования
. (1)
Аналогично по другим осям
, (2)
. (3)
Геометрические соотношения. Формулы Коши
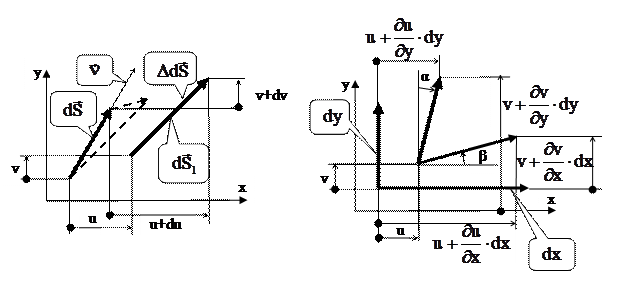
Бесконечно малый отрезок – вектор 
, направленный по направлению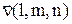 
после нагружение перемещается в положение 
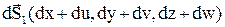. Представим результат перемещения как прибавление вектора 
. Тогда приращение длины вектора, выбранного в направлении 
, есть скалярное произведение 
, поделив которое на 
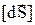,вычисляем линейную деформацию в выбранном направлении
.
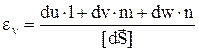Но: 
, 
, 
, а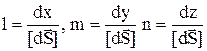 
, и, окончательно, получаем
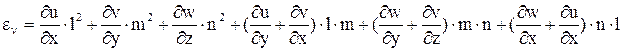
Физический смысл первых трех членов очевиден. Например, при 
получаем линейную деформацию отрезка, направленного по оси x, т.е. 
. (4)
Аналогично 
, (5) и 
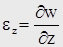. (6)
Остальные три члена – угловые деформации. Действительно, например,
, но 
.
Аналогично 
. Т.е. в малых деформациях
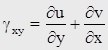(7). Аналогично 
(8), 
(9).
Таким образом, деформированное состояние в точке определяется шестью параметрами – линейными деформациями по координатным осям и угловыми деформациями в координатных плоскостях. В произвольном направлении имеем
