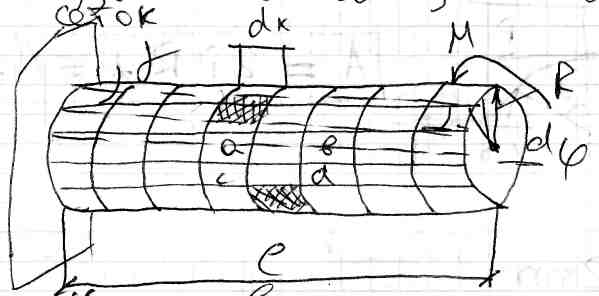
Для того, чтобы определить, какие напряжения возникают в материале при кручении стержней круглого сечения, рассмотрим характер поведения материала, т.е. рассмотрим как протекает деформация материалов. Будем использовать метод сеток.
|
Кольцевые лини сетки – следы поперечных сечений на боковой поверхности стержня. Горизонтальные линии сетки – следы слоев (образующих) на боковой поверхности стержня. Расстояние между кольцами не уменьшилось, образующие повернулись относительно начального положения на угол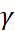 
. Радиус на торцевой поверхности прямолинейный до нагружения остался прямолинейным и в процессе нагружения и повернулся на угол 
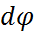. На основании анализа поведения сетки, устанавливаем:
1. Поперечные сечения стержня, плоские до нагружения, остаются плоскими и в процессе нагружения и поворачиваются на некоторый угол относительно своего первоначального положения, т.е. в упругом состоянии выполняется гипотеза плоских сечений.
2. Неизменность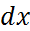 
указывает на то, что длина стержня при нагружении не изменяется, и нормальные напряжения в направлении продольной оси отсутствуют.
3. Квадратики сетки до нагружения при нагружении принимают ромбическую форму.
Поэтому при кручении стержней круглого поперечного сечения материал испытывает деформацию чистого сдвига. Таким образом в материале возникают касательные напряжения.
|
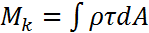
И должен быть равен внешнему моменту. Из полученного выражения определить касательные напряжения не представляется возможным, так как неизвестен закон их распределения по площади поперечного сечения, но так как материал испытывает деформацию чистого сдвига, то касательные напряжения могут быть определены по закону Гука 2-го рода: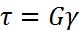 
. Для того, чтобы определить 
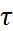по закону Гука, необходимо определить относительную сдвиговую деформацию. Для этого из стержня выделим объем в виде сектора.
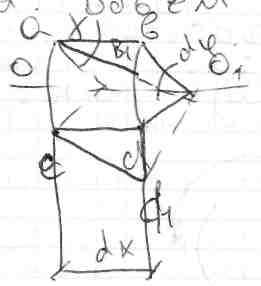
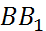– общая сторона двух треугольников 
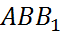и 
И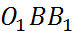з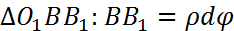 
;
Из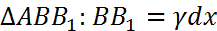 
;
Из этих двух уравнений следует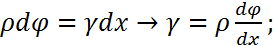 
- закон Гука при кручении стержней круглого поперечного сечения.
Подставим 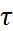в выражение для крутящего момента:
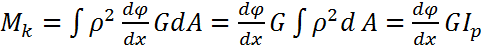, где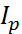 
- полярный момент инерции.
48 Деформации бруса круглого сечения. Жесткость при кручении. Эпюра углов закручивания. В любом круговом слое поперечного сечения скручиваемого стержня возникают касательные напряжения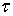 
, которые для цилиндрического стержня можно определить по формуле 
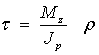. Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения.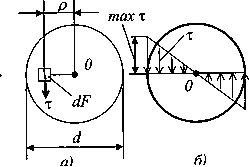 
В плоскостях сечений радиальные линии образуют углы поворота сечений φ1 и φ2. Угол ФИ1 свидетельствует о сдвиговой деформации волокон на участке стержня длинной Z, а угол ФИ2 – на участке Z – dz. Приращение угла поворота ФИ на участке стержня dz составляет величину dφ, которую называют углом закручивания стержня, т.е. абсолютной угловой деформацией при кручении. Относительной деформацией при кручении явл. величина θ= dφ/dz.Здесь 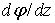 — погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a)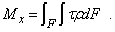 
| (2) |
Если в круговом слое скручиваемого стержня обнаружена сдвиговая деформация, то в нем должны возникнуть касательные напряжения, которые по закону Гука составлют τ=Gγ или τ=Gρθ. В центре сеченя напряжения отсутствуют.Относительный угол закручивания пропорционален крутящему моменту в сечении и обратно пропорционален жесткости сечения скручиваемого стержня GIp.Для обеспечения необходимой жесткости производится проверка по условию жесткости вида θmax = Tmax/ (GIp) ≤θadm. Нормативные значения θadm находятся в пределах 0,15 – 2 град/м.
49. Главные напряжения, расчеты на прочность и жесткость, условие прочности. Если скручив. cтержень выполнен из пластичного материала, разрушение происходит от чрезмерных сдвиговых деформаций в поперечных сечениях, развивающихся в поверхностных слоях.Расчетное условие имеет вид: тmax=(Tmax/Ip)ρmax=Tmax/Wp≤RsγcRs – расчётное сопротивление материала сдвигу (Rs=(0.55-0.6)R)Если скручивается стержень из хрупкого материала, то воспользуемся второй теорией прочности (теория наибольших относительных удлинений τmax=Tmax/Wp≤Rtγc/(1+ν), где v – коэффициент Пуассона.Условия прочности при кручении: т=Mzmax/Wp≤[т] Θ=Mzmax/GIp2)Проектный расчет (подбор сечений валов)3)Расчет на грузоподъемность, определяется допускаемая величина крутящего момента.Условие жесткости заключается в том, что угол закручивания единицы длины вала не должен превышать определенную величину.Это условие необходимо учитывать, чтобы избежать явл. пружинения при остановке валов.Допускаемый угол закручивания 1 метра вала Фи0:ФИо≥180*Mz/(Пи*GIp)=ФИ
51. Кручение бруса некруглого поперечного сечения: напряжения, деформации, геометрич. Характеристики, эпюра касательных напряжений для бруса прямоугольного поперечного сечения. Для некруглых поперечных сечений гипотеза плоских сечений неприемлима.Поперечные сечения существенно искривлены и в результате существенно изменяется картина распределения напряжений.Отметим некоторые особенности распределения законов напряжений некруглой формы:
1) если поперечное сечение имеет внешние углы, то в них касательные напряжения должны обращаться в 0
2) если нагруженная поверхность бруса при кручении свободна, то касат. Напряжения, направленные по нормали к контуру так же будут = 0.тA = тmax = Mz/Wk Wk = ρ(b в кубе)Для определения наибольших напряжений и деформаций закручивания пользуются решениями Сен-Ванана:τhmax = T/Wt, Δφ = Tl/(GIt)На рис. 4.3 показана, полученная методом теории упругости, эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как видно, напряжения равны нулю, а наибольшие их значения возникают по серединам больших сторон: в точке А A max =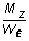 
, где WК = b 3 аналог полярного момента сопротивления поперечного сечения прямоугольного бруса; в точке В B max ,
здесь необходимо учесть, что b малая сторона прямоугольника.Значения угла закручивания определяется по формуле: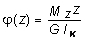 
, (4.16)
где IK = b 4 аналог полярного момента инерции поперечного сечения бруса.Коэффициенты , и зависят от отношения сторон m = h / b, и их значения приведены в табл. 3.
Таблица 3
| m | 1,5 | 2,0 | 3,0 | 6,0 | ||
| | 0,141 | 0,294 | 0,457 | 0,790 | 1,789 | 3,123 |
| | 0,208 | 0,346 | 0,493 | 0,801 | 1,789 | 3,123 |
| | 1,000 | 0,859 | 0,795 | 0,753 | 0,743 | 0,742 |
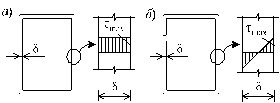
52. Кручение тонкостенного бруса замкнутого и открытого профилей В машиностроении, авиастроении и вообще в технике широко применяются тонкостенные стержни с замкнутыми (рис. 4.7, а) и открытыми профилями (рис. 4.7, б) поперечных сечений. Поэтому расчеты на кручение таких тонкостенных стержней имеет большое практическое значение.
Ðèñ. 4.7
|
Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров (длиной срединной линии контура поперечного сечения и длины стержня).
Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.Обращаясь к формулам (4.14), (4.16) и при предельном переходе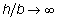 
, получим: 
; 
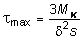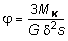, где толщина профиля; s длина контура профиля; l длина стержня.В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i ом произвольном участке: 
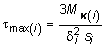, (4.18)
где MK (i) доля крутящего момента, соответствующего i му участку: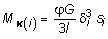 
,
где угловое перемещение, единое для всех участков: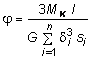 
.рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент через напряжения , выполняя операцию контурного интегрирования получим: 
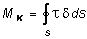. (4.20)
Из условия равновесия сил по оси z выделенного элемента длиной dz (4.9) легко установить, что по контуру сечения произведение является постоянной величиной. С учетом данного обстоятельства, выражение примет вид: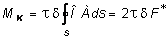 
,
где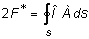 
представляет собой удвоенной площадь, ограниченную срединной линией контура сечения.Из (4.21) наибольшее напряжение определяется по формуле: 
. (4.22)
Для вывода выражения для угла закручивания воспользуемся энергетическими соображениями. Энергия, накопленная в элементарном объеме с размерами , dz, ds за счет деформаций чистого сдвига, равна: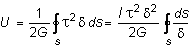 
.С учетом последнее выражение можно представить в виде:
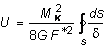.С другой стороны, работу внешних сил можно представить в виде: 
.
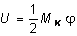Приравнивая оба выражения из и получим: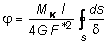 
,
Если является постоянной по контуру, будем иметь: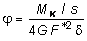 
,
где s длина замкнутого контура.
53. Потенциальная энергия при кручении. Потенциальная энергия деформации при кручении определяется подобно тому, как это делалось при растяжении и сдвиге.Удельная потенциальная энергия деформации при чистом сдвиге определяется из уравнении:
 .
|
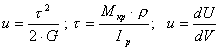Потенциальная энергия деформации U определится из уравнения путем интегрирования по объему:
 .
|
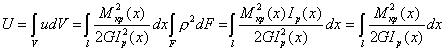При этом учитывалось, что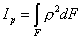 
. В брусе постоянной жесткости GIp при действии постоянного по длине крутящего момента, имеем
 .
|
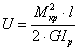54. Статически неопределимые задачи при расчетах на кручение. Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия,называются статически неопределимыми. По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними. Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.На рис. 2.5, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А, т.е. x = 0, y = 0. Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N 1 и N 2 в которой количество уравнений равно количеству неизвестных: N 1 N 2 sin = 0; N 2 cos Р = 0.
Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N 1, N 2 и N 3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.В общем случае под n раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия на n единиц. Решение статически неопределимых задач методом сил проводится в такой последовательности.1. Устанавливается степень статической неопределимости системы как разность между числом искомых неизвестных усилий и числом независимых уравнений равновесия. При этом учитывается, что простой шарнир, соединяющий два стержня системы, уменьшает степень статической неопределимости на единицу, так как снимает одну связь, препятствующую повороту одной части системы относительно другой. Тем самым простой шарнир позволяет добавить к уравнениям равновесия всей системы уравнение равновесия присоединенной этим шарниром части системы.2. Из заданной статически неопределимой системы выделяется основная система путем удаления лишних связей и внешней нагрузки.В качестве лишних могут быть выбраны различные связи. Поэтому для одной и той же статически неопределимой системы можно получить сколько угодно основных систем. Но любая основная система должна быть обязательно геометрически неизменяемой и статически определимой.Нельзя выбирать в качестве основной и мгновенно геометрически изменяемую систему, потому что в такой системе при любой сколь угодно малой нагрузке усилия получаются бесконечно большими или неопределенными.3. Изображается соответствующая выбранной основной эквивалентная система, в которой взамен снятых лишних связей и в их направлении приложены силы Xi, если связи препятствовали линейному перемещению, и пары Xk, если они исключали повороты сечений.4. Составляются канонические уравнения метода сил.5. Вычисляются коэффициенты канонических уравнений аналитически
