Внутренние силы и напряжения

Моменты инерции сечения

Рис. 3.3

В дополнение к статическим моментам в системе координат x0y (рис. 3.1)рассмотрим три интегральных выражения:

(3.7)

Первые два интегральных выражения называются севыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y. Для сечений, состоящих из n-числа областей (рис. 3.3), формулы (3.7) по аналогии с (3.6) будут иметь вид:

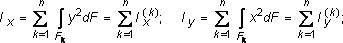
Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 3.2). Преобразуя формулы (3.7) с учетом выражения (3.2), получим:

(3.8)

Если предположить, что оси x1 и y1 (см. рис. 3.2) являются центральными, тогда и выражения (3.8) упрощаются и принимают вид:

(3.9)

Рис. 3.4

Определим осевые моменты инерции прямоугольника относительно осей x и y, проходящих через его центр тяжести (рис. 3.4). В качестве элементарной площадки dF возьмем полоску шириной b и высотой dy (рис. 3.4). Тогда будем иметь:

Аналогичным образом можно установить, что: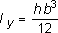

Для систем, рассматриваемых в полярной системе координат (рис. 3.5, а), вводится также полярный момент инерции:

где r - радиус-вектор точки тела в заданной полярной системе координат.

Рис. 3.5

Вычислим полярный момент инерции круга радиуса R. На рис. 3.5, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью

dF = r dr dj.

Интегрирование по площади заменим двойным интегрированием:

.Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 3.5, б), что

r2 = x2 + y2,

следовательно,

Так как оси x и y для круга равнозначны, то Ix = Iy = .

Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):

12. Главные оси и главные моменты инерции Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рис. 3.5, б легко установить, что

u = y sin a + x cos a; v = y cos a - x sin a. (3.10) Из выражений:

с учетом (3.10) после несложных преобразований получим:

(3.11)

Складывая первые два уравнения, получим:

Iu + Iv = Ix + Iy = Ir, (3.12)

Где ; Ir - полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей.

Дифференцируя в (3.11) выражение Iu по a и приравнивая его нулю, находим значение a = a0, при котором функция Iu принимает экстремальное значение:

(3.13)

С учетом (3.12) можно утверждать, что при a = a0 один из осевых моментов Iu или Iv будет наибольшим, а другой наименьшим. Одновременно при a = a0 Iuv обращается в нуль, что легко установить из третьей формулы (3.11).

Декартовы оси координат, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными и определяются из (3.11) с учетом (3.13) и имеют вид:. (3.14)

Момент сопротивления относительно некоторой оси – величина равная мо-менту инерции относительно той же оси отнесенному к расстоянию (y_max или z_max) до наиболее удаленной от этой оси точкиW y= Iy/zmax; Wz=Iz/ymax. Размерность моментов сопротивления метры кубические в СИ Радиусом инерции сечения относительно некоторой оси, называется величи-на, определяемая из соотношения:

iz=√Iz/ Fiy=√Iy/F Радиус инерции выражается в м в системе СИ

13 Осевые моменты сопротивления для простейших сечений (Ixc и Iyc - центральные моменты инерции сечений):

1. Для прямоугольника (рис. 4.10).

2. Для треугольника (рис.4.11).

(для верхних волокон).

Аналогично можно вычислить моменты сопротивления относительно оси у левых и правых волокон Wул,Wуп

3. Для круга (рис. 4.12).

4. Для полукруга (рис.4.13).

5. Для трубчатого сечения (рис. 4.14).

Полярный момент сопротивления для трубчатого сечения.

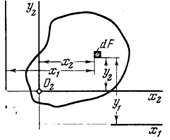
14. Парал перенос При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей, x₁, y₁ и x₂, y₂.Пусть расстояние между осями x₁ и x₂ равно b, а между осями y₂ и y₂ равно а (рис. 2). Положим, что площадь сечения F и статические моменты относительно осей x₁ и y₁, т. е. S_x1, и S_y1 заданы. Требуется определить S_x2 и S_y2.

Очевидно, х₂ = x₁ — а, y₂ = y₁ — b. Искомые статические моменты будут равны

или

Таким образом, при параллельном переносе осей статический момент меняется на величину, равную произведению площади F на расстояние между осями.

Рассмотрим более детально, например, первое из полученных выражений:

Величина b может быть любой: как положительной, так и отрицательной. Поэтому ее всегда можно подобрать (причем единственным образом) так, чтобы произведение bF было равно S_x1.Тогда статический момент S_x2, относительно оси x₂обращается в нуль.

Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной, и расстояние до этой оси от некоторой, произвольно взятой, оси х₁равно

Рис. 2

Аналогично для другого семейства параллельных осей

Точка пересечения центральных осей называется центром тяжести сечения. Путем поворота осей можно показать, что статический момент относительно любой оси, проходящей через центр тяжести, равен нулю.

Нетрудно установить тождественность данного определения и обычного определения центра тяжести как точкиприложения равнодействующих сил веса. Если уподобить рассмотренное сечение однородной пластинке, то сила веса пластинки во всех точках будет пропорциональна элементарной площади dF, а момент сил веса относительно некоторой оси — пропорционален статическому моменту. Этот момент сил веса относительно оси, проходящей через центр тяжести, равен нулю. В нуль обращается, следовательно, и статический момент относительно центральной оси.

Поворот осей

ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

Рис. 3

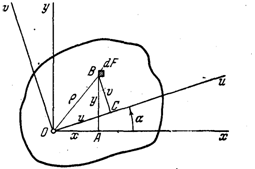Требуется определить J_u, J_v, J_uv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол a (рис. 3).

Проектируем замкнутый четырехугольник ОАВСО на оси и и v. Так как проекция ломаной линии равна проекции замыкающей, находим:

u = y sin a +x cos a, v = y cos a — x sin a

В выражениях (3), подставив вместо x₁ и y₁ соответственно u и v, исключаем u и v

С изменением угла поворота осей a каждая из величин J_u и J_v меняется, а сумма их остается неизменной. Следовательно, существует такое a, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.

Дифференцируя выражение J_u (5) по a и приравнивая производную нулю, находим

При этом значении угла a один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции J_uv при указанном угле a обращается в нуль, что легко устанавливается из третьей формулы (5).

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными, то тогда они называются главными центральными осями.

Верхний знак соответствует максимальному моменту инерции, а нижний — минимальному. После того как сечение вычерчено в масштабе и на чертеже показано положение главных осей, нетрудно установить, которой из двух осейсоответствует максимальный и которой — минимальный момент инерции.

Если сечение имеет ось симметрии, то эта ось всегда будет главной.Центробежный момент инерции части сечения, расположенной по одну сторону от оси, будет равен моменту части, расположенной по другую сторону, но противоположен ему по знаку. Следовательно, J_ху= 0 и оси х и у являются главными.

16. Удлинение стержня и закон Гука Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l -после нагружения она стала равной l + Dl (рис. 2.2). Величину Dl называют абсолютным удлинением стержня.

Рис. 2.2 Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной (2.1)

Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.2). При растяжении он увеличит свою длину на величину D dz и его деформация составит: (2.2) В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:s = E e. (2.3) Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим: ,откуда с учетом того, что и ,окончательно получим: Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим (2.5) При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций: , где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:.

17. Коэффициент Пуассона характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах (мм/мм, м/м))

где ν — коэффициент Пуассона.

— деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия)

— продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия).

Внутренние силы и напряжения

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня. Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.1, б), приходим к следующему уравнению: P + Nz = 0,откуда следует, что Nz = P = const. Примем для Nz следующее правило знаков. Если Nz направлена от сечения, т.е. вызывает положительную деформацию (растяжение), то она считается положительной. В обратном случае - отрицательной.

Рис. 2.1

Нормальная сила Nz приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:

Но из этой формулы нельзя найти закон распределения нормальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.1, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации. Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны , где F - площадь поперечного сечения стержня.Высказанное предположение о равномерном распределении внутренних сил в попер сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади попер сечения (рис. 2.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механ характ-ик конструкций. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Эпюрами прод сил и норм напряжений назыв графики, показыв законы изменения сил и напряжений в попер сечениях по длине стержня.

19 Концентрация напряжений - в теории упругости - положение, согласно которому уравновешенная система сил, приложенных к какой-либо части твердого тела, вызывает в нем напряжения, быстро убывающие по мере удаления от этой части, и может быть заменена эквивалентной системой сил. Концентрация напряжений Вблизи различного рода отверстий, надрезов, выточек и, вообще,(мест резкого изменения поперечных размеров распределение напряжений становится существенно неравномерным, и возникают зоны повышенных напряжений.

Явление возникновения значительных местных напряжений называется концентрацией напряжений, а причина, вызвавшая концентрацию - концентратором напряжений. Концентрация напряжений характеризуется коэффициентом концентрации α. Величину α также называют теоретическим коэффициентом концентрации. Коэффициентом концентрации α называется отношение действительного напряжения σmax в наиболее напряженной точке к номинальному напряжению σn в той же точке, т. е. или 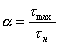. Номинальными называются напряжения, вычисленные по формулам сопротивления материалов, не учитывающим явление концентрации напряжений. В тех случаях, когда возникают трудности в вычислении номинальных напряжений в сечении с концентратором напряжений, за номинальные принимают напряжения в неослабленном сечении детали. В настоящее время методами теории упругости и экспериментальными методами (обычно путем испытания образцов из оптически активного материала в поляризованном свете) определены величины коэффициентов концентрации для многих практически важных случаев. Расчетные формулы, таблицы и графики для определения коэффициентов концентрации приводятся в справочной литературе.

Концентраторы напряжений – местные резкие изменения однородности (формы и, следовательно, жесткости) конструкции, приводящие к резкому местному (локальному) повышению напряжений в конструкции.

Обобщенный закон Гука

Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного, и как частый случай, плоского напряженных состояний.

Он может быть получен на основании з-на Гука для линейного напряжен состояния и принципа независимости действия сил.

Пусть задано произвольное объемное напряж состояние с главными напряжениями , и . Представим его в виде суммы 3х линейных напряженных состояний. Учитывая, что при линейном напряженном состояни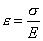и и запишем выражение для лин относит деформации в направлении :

Деформации в направлении действия главных напряжений равны

Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации , , , в направлении главных напряжений называются главными деформациями.

Соотношения обобщенного закона Гука могут быть записаны для любых (не главных) площадок, но т.к. при этом будут действовать, кроме нормальных и касательные напряжения (рис.3.10), то необходимо добавить три соотношения для вычисления угловых деформаций. Таким образом, для произвольных площадок обобщенный закон Гука содержит 6 соотношений, связывающих деформации и напряжения: