Практический тепловой баланс в общем случае определяется простым уравнением
,
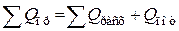где Q пр– физическое тепло, вносимое в аппарат реагентами, материалом аппарата (для периодических процессов), тепло фазовых переходов, тепло реакции и т. д.;
Q расх – физическое тепло, уносимое из аппарата продуктами реакции;
Q пот – тепло, теряемое в окружающую среду.
При неизвестных размерах аппарата точное определение величин тепла, теряемого в окружающую среду, невозможно. В этом случае принимают Q пот равным 3-5 % от максимального значения суммы вносимого или уносимого тепла. Если геометрические размеры аппарата известны, то можно оценить потери тепла по уравнению теплоотдачи
где Q – поток потерянного тепла, Вт;
F – наружная поверхность теплообмена аппарата, кв.м;
aп – наружный коэффициент теплоотдачи, Вт/(кв.м·К);
t п – температура наружной поверхности аппарата, °С;
t о – температура окружающей среды, °С.
Температура наружной поверхности аппарата либо определяется из санитарных условий (<50 °С), либо задается условиями работы аппарата. Температура окружающей среды выбирается минимальной для данного помещения или района (при установке оборудования на открытом воздухе). Наружный коэффициент теплоотдачи рассчитывается по двум составляющим:
aн = aк + aл,
где aк – коэффициент теплоотдачи конвекцией;
aл – коэффициент теплоотдачи лучеиспусканием.
Конвективный коэффициент теплоотдачи зависит от места установки оборудования и от его положения в пространстве.
Горизонтальные трубопроводы и оборудование внутри помещений: при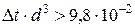 
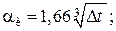
при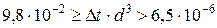 
,
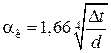где d – наружный диаметр аппарата.
Для вертикальных аппаратов и трубопроводов внутри помещения:
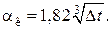
При установке оборудования на открытом воздухе:
– для плоских стенок
,
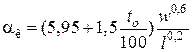где w – скорость ветра, м/с;
l – длина стенки по направлению ветра, м;
– для аппаратов
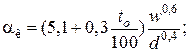
– для горизонтальных трубопроводов
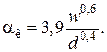
Коэффициент теплоотдачи лучеиспусканием (температура в К)
,
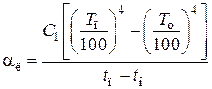где C 1 – степень черноты поверхности аппарата или трубопровода.
В случае расчета теплоизоляции аппарата или трубопровода, величина Q будет допустимой потерей тепла в окружающую среду. Тогда толщину слоя теплоизоляции можно рассчитать по формуле
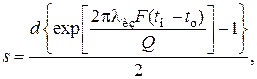
где lиз – коэффициент теплопроводности материала изоляции.
Рассмотрим расчет теплового баланса на примере.
Пример 9.2. Определить температуру реакционной смеси процесса окисления метанола до формальдегида на входе в реактор, полагая температуру на выходе из реакционной зоны равной 800 °С. Результаты материальных расчетов взять из примера 4.3. Теплоемкости компонентов реакции принять средними при температуре 650 °С.
Решение: Определим теплоемкости компонентов процесса. Из справочника [18] выпишем стандартные энтальпии образования и температурные зависимости теплоемкостей всех веществ, участвующих в процессе.
Для всех реакций процесса рассчитаем энтальпию реакции:
реакция (1) –115,9-241,84+201,2+0,5·0=-156,54 кДж/моль;
реакция (2) -115,9-0+201,2=85,3 кДж/моль;
реакция (3) -110,5-2·0+201,2=126,35 кДж/моль;
реакция (4) -74,85-241,84+201,2=-115,49 кДж/моль;
реакция (5) -376,7-241,84+115,9=-502,64 кДж/моль;
реакция (6) -393,51-241,84+115,9+1,5·0=519,45 кДж/моль.
Тогда уравнения реакций с термохимическим правилом знаков (тепловой эффект в кДж/моль) примут вид:
CH3OH+1/2O2=CH2O+H2O+156,54; (1)
CH3OH=CH2O+H2-85,3; (2)
CH3OH=CO+2H2-126,35; (3)
CH3OH+H2=CH4+H2O+115,49; (4)
CH3OH+O2=HCOOH+H2O+502,64; (5)
CH3OH+1,5O2=CO2+2H2O-519,45. (6)
На основании материального баланса рассчитаем мольный расход метанола по каждой из реакций системы, а затем и количество выделяемого или поглощаемого тепла (см. табл. 9.2.), откуда тепловой эффект процесса будет равен 604,8 кВт.
Таблица 9.1. Энтальпии образования и температурные зависимости теплоемкости
| Компонент | DH0, кДж/моль | Теплоемкость, Дж/(моль·К) | |||
| a | b ·103 | c· 106 | c ’·10-5 | ||
| Кислород | 31,46 | 3,30 | - | -3,77 | |
| Азот | 27,87 | 4,27 | - | - | |
| СО | -110,5 | 28,41 | 4,10 | - | -0,46 |
| СО2 | -393,51 | 44,14 | 9,04 | - | -8,53 |
| Водород | 27,28 | 3,26 | - | 0,502 | |
| Вода | -241,84 | 30,00 | 10,71 | - | 0,33 |
| Метанол | -201,2 | 15,28 | 105,2 | -31,04 | - |
| Метан | -74,85 | 17,45 | 60,46 | 1,117 | - |
| СН2О | -115,9 | 18,82 | 58,38 | -15,61 | - |
| НСООН | -376,7 | 19,4 | 112,8 | -47,5 | - |
Таблица 9.2. К расчету суммарного теплового эффекта процесса
| Номер реакции | Расход метанола, кмоль/ч | Тепло реакции, кДж/моль | Расход тепла, кВт |
| (1) | 23,95 | 156,54 | |
| (2) | 16,75 | -85,3 | -397 |
| (3) | 0,154 | -126,35 | 5,4 |
| (4) | 0,456 | 115,49 | -14,6 |
| (5) | 2,75 | 502,64 | -384 |
| (6) | 2,45 | -519,45 | |
| Итого: | 63,93 | 604,8 |
Таблица 9.3. Средние теплоемкости компонентов реакции
| Компонент | Теплоемкость, Дж/(моль·К) | Теплоемкость, Дж/(кг·К) |
| Кислород | 31,46 | |
| Азот | 27,87 | |
| СО | 28,41 | |
| СО2 | 44,14 | |
| Водород | 27,28 | |
| Вода | 30,00 | |
| Метанол | 15,28 | |
| Метан | 17,45 | |
| СН2О | 18,82 | |
| НСООН | 19,40 |
Составим тепловой баланс процесса окисления метанола, предварительно рассчитав теплоемкости.компонентов при заданной температуре 650 ° С по уравнениям
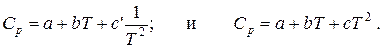
Данные расчета занесены в табл. 9.3.
Физическое тепло, вносимое компонентами в реактор:
с метанолом 1860·2,44·t/3600=1,2607· t кВт;
с кислородом 586·1,05·t/3600=0,1709 ·t кВт;
с азотом 1920·1,12·t/3600=0,5973 ·t кВт.
Всего на входе в реактор 2,0289· t кВт.
Таблица 9.4. Тепловой баланс процесса получения формальдегида
| ПРИХОД ТЕПЛА | РАСХОД ТЕПЛА | |||||
| Статьи | КВт | % | Статьи | КВт | % | |
| Спирто-воздушная смесь: Метанол Кислород Азот Тепло реации Ошибки округления | 650,5 88,2 308,2 604,8 0,2 | 39,38 5,34 18,66 36,61 0,01 | Формальдегид Метанол Водяной пар НСООН СО2 СО Метан Водород Азот Потери тепла | 493,4 201,7 207,7 47,8 27,1 1.1 6,6 109,9 477,9 78,7 | 29,87 12,21 12,57 2,89 1,64 0,07 0,40 6,65 28,93 4,77 | |
| ИТОГО: | 1651,9 | ИТОГО: | 1651,9 | |||
Физическое тепло, уносимое компонентами из реакционной зоны:
с формальдегидом 1220·1,82·800/3600=493,4 кВт;
с метанолом 372·2,44·800/3600=201,7 кВт;
с водяным паром 572·2,13·800/3600=207,7 кВт;
с уксусной кислотой 126,5·1,7·800/3600=47,8 кВт;
с диоксидом углерода 108·1,13·800/3600=27,1 кВт;
с оксидом углерода 4,3·1,13·800/3600=1,1 кВт;
с метаном 7,3·4,05·800/3600=6,6 кВт;
с водородом 34,1·14,5·800/3600=109,9 кВт;
с азотом 1920·1,12·800/3600=477,9 кВт;
Всего на выходе – 1573,2 кВт.
Примем потери тепла в количестве 5 % от его расхода. Составим уравнение теплового баланса, из которого определим температуру на входе в реактор:
2,0289·t+604,8=1573,2+0,05·1573,2.
t =(1,051573,2-604,8)/2,0289=516 °C.
Занесем результаты расчета в табл. 9.4.
Пример 9.3. Произвести тепловой расчет и составить тепловой баланс колонны синтеза аммиака в соответствии с исходными данными:
температура в зоне реакции t =500 °C;
количество газовой смеси на входе в колонну V 1 =119025 нм3/ч;
температура газовой смеси на входе t 1=35 °С;
количество газовой смеси на выходе из колонны V 2 =102329 нм3/ч;
температура газовой смеси на выходе t 2=110 °С.
Состав газовой смеси
| Компонент | Состав газовой смеси, % по объему | |
| на входе | на выходе | |
| Водород | 74,1 | 62,06 |
| Азот | 24,7 | 20,7 |
| Аммиак | 1,2 | 17,24 |
Количество образующегося аммиака GNH 3=12500 кг/ч.
Рабочее давление в аппарате Pp =30 МПа.
Температура воды
на входе 200 °С;
на выходе 374 °С.
Решение. (Исходные данные и физико-химические свойства компонентов взяты из литературы [11, 49, 120].)
Составим уравнение теплового баланса
.
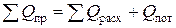Приход тепла в колонну синтеза аммиака (S Q пр).
1) С газовой смесью
,
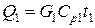где G 1 – количество поступающей газовой смеси, кмоль/ч;
Ср 1 – ее мольная теплоемкость, Ср 1=31,0 кДж/(кмоль×К).
Откуда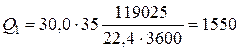 
кВт.
2) Тепловой эффект реакции синтеза аммиака при высоком давлении. Определяется по уравнению
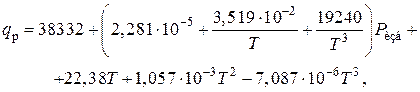
где q p – тепловой эффект реакции, кДж/кмоль;
Р изб – избыточное давление в реакторе, Па;
Т – температура, К.
В данном случае
Т =273+500=773 К;
Р =30×106 Па.
Откуда
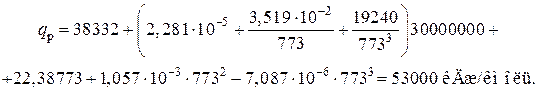
Общее количество тепла, выделяющееся при синтезе аммиака, будет
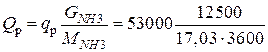=10806 кВт.
3) С охлаждающей водой на входе
,
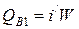где i / - энтальпия воды на входе при температуре 200 °С, равная 853 кДж/кг;
W – расход охлаждающей воды, кг/с.
Общий приход тепла в колонну синтеза аммиака
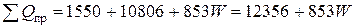кВт.
Расход тепла в колонне синтеза аммиака
1) Расход тепла, уносимого с газовым потоком, равен
,
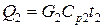где G 2 – количество уходящей газовой смеси, кмоль/ч;
Ср 2 – ее мольная теплоемкость, Ср 2=33,1 кДж/(кмоль×К).
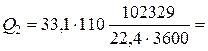4620 кВт.
2) Тепло, уносимое охлаждающей водой,
,
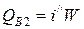где i // - энтальпия воды на выходе при температуре 374 °С, i //=2100 кДж/кг.
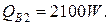
3) Потери тепла в окружающую среду можно принять равными 5 % от тепла, вносимого в колонну синтеза аммиака
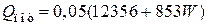кВт.
Общий расход тепла
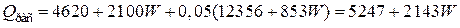кВт.
Уравнение теплового баланса
.
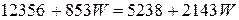Откуда расход охлаждающей воды будет равен
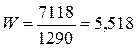кг/с.
Составим таблицу теплового баланса (табл. 9.5).
Таблица 9.5. Тепловой баланс колонны синтеза аммиака
| Приход тепла | Расход тепла | ||
| Статьи прихода | кВт | Статьи расхода | кВт |
| Газовая смесь Реакция синтеза Охлаждающая вода | Газовая смесь Охлаждающая вода Потери тепла | ||
| Итого | Итого |
Теплообмен в реакторах
При проведении реакции при постоянной температуре (изотермический процесс) степень превращения реагентов зависит от их концентрации и не зависит от температуры, поэтому уравнение материального баланса можно проинтегрировать и получить зависимость степени превращения от времени.
При неизотермическом проведении процесса (адиабатическом или программно регулируемом) приходится решать совместно уравнения материального и теплового баланса с учетом зависимости скорости реакции от температуры и, при необходимости, процесса теплопередачи.
Для создания приблизительно изотермических условий в реакторе можно применить несколько способов теплообмена:
- теплообмен при постоянной скорости теплопередачи; когда реактор обогревается топочными газами или пламенем, коэффициент теплопередачи изменяется мало, а температура настолько высока, что изменение температуры реагентов практически не влияет на температурный напор;
- теплообмен при постоянном коэффициенте теплопередачи; например, в аппаратах с мешалкой коэффициент теплопередачи зависит в основном от скорости перемешивания, которую можно держать постоянной, и скорость теплопередачи будет определяться изменением температуры реагентов;
- автоматическое регулирование скорости теплопередачи путем регулирования расхода теплоносителя или изменения температуры его фазового перехода, например за счет давления.
Последний способ, в принципе, является самым лучшим, но не всегда экономически целесообразным.
Теплообмен в реакторах смешения. Рассмотрим химическую реакцию
A+B=R+Δ H r,
где Δ H r – энтальпия реакции, Дж/моль.
Запишем уравнение теплового баланса, относя мольные энтальпии к некоторой температуре Т С, например 0 ºС, являющейся уровнем отсчета.
Начальная температура реагентов Т 0, конечная – Т:
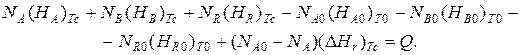
Q – количество отводимого или подводимого тепла, Дж.
Если отсутствуют фазовые превращения, то энтальпии компонентов можно выразить через теплоемкости:
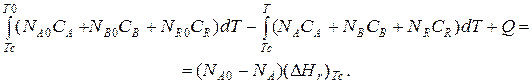
Если полагать, что теплоемкости не зависят от температуры в исследуемом интервале температур, а температура Т 0 является уровнем отсчета, то уравнение упростится:
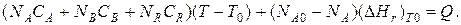
Зная состав исходной смеси, можно связать степень превращения и температуру. Для стехиометрической смеси, разделив последнее уравнение на N A 0, получим:
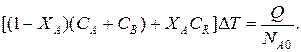
После преобразований
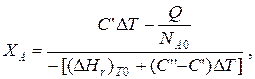
где С' и С' ' – сумма теплоемкостей реагентов и продуктов реакции соответственно. Но, так как
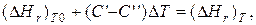
то
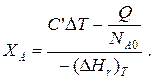
Здесь у энтальпии реакции и теплоты термодинамическое правило знаков,
т. е. тепло, подводимое к системе, считается положительным.
Для адиабатических условий Q =0, поэтому
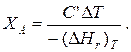
Пример 9.4. Для реакции первого порядка А+В=R, протекающей в адиабатических условиях, известны следующие данные: Т 0=28 ºС; NA 0 =NB 0=1 кмоль; N R0=0; СА=СВ =125 Дж/(моль·К); CR =167 Дж/(моль·К) ;
H = -11600 Дж/моль. Константа скорости реакции в узком интервале температур зависит линейно от температуры
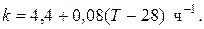
Определить степень превращения реагентов и время ее достижения, если температура в реакторе повысилась за счет реакции на 28 К?
Решение: Полагая отсутствие фазовых превращений в процессе, составим уравнение теплового баланса
[(1- XA)(125+125)+167 XA ](T - 28)-11600 XA =0;
(250-83 XA)(T -28)=11600 XA;
T -28=28=11600 XA /(250-83 XA);
XA =0,503.
Определим время реакции из баланса массы при условии реакции первого порядка
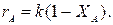
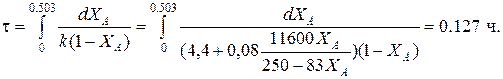
(Последний интеграл вычислен численным методом по формуле Симпсона.)
Составим тепловой баланс в дифференциальной форме, полагая, что за элементарное время d t скорость реакции r A и скорость теплопередачи R определяются уравнениями
;
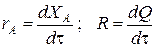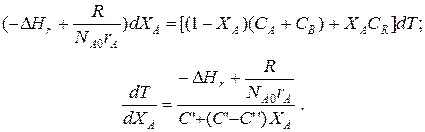
Теплоемкость и скорость реакции являются известными функциями температуры. Если скорость теплопередачи задана в функции от температуры, то последнее уравнение можно проинтегрировать. Для трех рассмотренных способов теплообмена связь между температурой и скоростью теплопередачи имеет вид:
- теплообмен при постоянной скорости теплопередачи
R = const;
- теплообмен при постоянном коэффициенте теплопередачи
R=KS(T т -T), KS =const, T т=const;
- автоматическое регулирование скорости теплопередачи
R =D Hr · rA = KS (T т- T), T =const.
Здесь: K – коэффициент теплопередачи, Вт/(м2*К);
S – поверхность теплопередачи, м2;
T т – температура теплоносителя.
Пример 9.5. Для реакции первого порядка известны следующие данные: энтальпия реакции D Hr = 11600Дж/моль; константа скорости реакции k =0,8 ч-1; коэффициент теплопередачи К =51 Вт/(м2·К); начальная загрузка реагента N A0=2270 моль. Определить поверхность теплообмена, необходимую для поддержания постоянной температуры t =49 ºС до конечной степени превращения XA =70 %. Нагрев осуществляется паром, температуру которого Т т можно регулировать в пределах от 110 до 177 ºС.
Решение: Скорость подвода тепла должна быть наибольшей в начале процесса, когда ХА =0, а скорость реакции – наибольшая. Расчет будем производить, используя уравнение
D Hr·r A= KS 1(T т -T).
Откуда максимальная поверхность теплопередачи в этот момент выразится уравнением
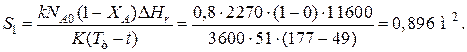
При такой поверхности и конечной степени превращения ХА =0.7 температура теплоносителя должна быть равна
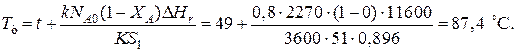
Эту температуру не обеспечить паром заданных параметров. Степень превращения, отвечающая наиболее низкой заданной температуре теплоносителя 110 ºС, при поверхности теплопередачи S 1 составит
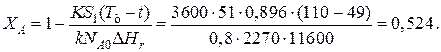
При температуре теплоносителя 110 ºС и степени превращения 0,7 имеем
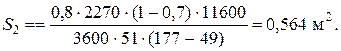
При ХА =0.524 и S2 =0.564 м2 имеем
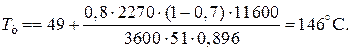
Таким образом, нагреватель должен состоять из двух параллельных змеевиков, один из которых с поверхностью S1 =0,564 м2, а другой –
S2 =0,896 - 0,564=0,332 м2. При снижении температуры пара до 110 ºС змеевик с поверхностью 0,332 м2 следует отключить.
Кривые регулирования строятся по уравнениям
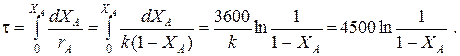
При ХА £0.52 ТТ =49+128(1- ХА);
при ХА >0.52 ТТ =49+203(1- ХА).
|
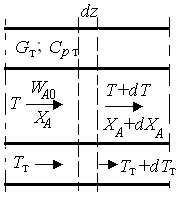
| Рис. 9.2. К расчету теплообмена в реакторе вытеснения |
Теплообмен в реакторах вытеснения. Если полагать отсутствие в реакционной зоне реактора идеального вытеснения радиальных градиентов температур, то можно составить три уравнения, одно из которых – баланс массы, второе – баланс тепла по реакционной массе и третье – баланс тепла по теплоносителю. Схема тепло- и массообмена в элементе реактора представлена на рис. 9.2.
Уравнение баланса массы
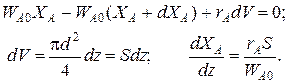
Уравнение баланса тепла в элементе реакционной зоны
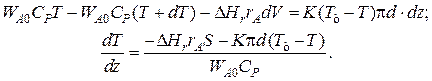
Уравнение баланса тепла в элементе рубашки
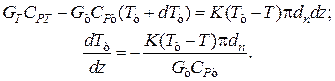
Совместное решение системы из трех дифференциальных уравнений дает возможность определить распределение степеней превращения, температур реакционной смеси и теплоносителя по длине реактора идеального вытеснения.
Для адиабатического реактора идеального вытеснения получаем систему из двух дифференциальных уравнений
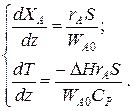
Пример 9.6. В гомогенном реакторе идеального вытеснения, представляющем собой трубу внутренним диаметром 50мм, протекает адиабатическая реакция второго порядка. Кинетические параметры реакции: энергия активации Е =58200 Дж/моль, k 0=2·107 м3/(моль·ч). Начальная концентрация реагента 20 кмоль/м3, его мольный расход 60 кмоль/ч, теплоемкость реакционной смеси 125 Дж/(моль·К). Энтальпия реакции
D Hr = - 10000 Дж/моль. Определить длину реактора при 90 %-ной степени превращения, если начальная температура реагентов 77 ºС.
Решение: Подставим исходные данные в систему дифференциальных уравнений материального и теплового баланса адиабатического реактора:
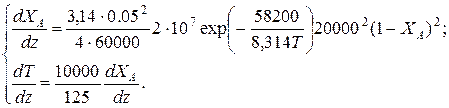
После преобразований получим:
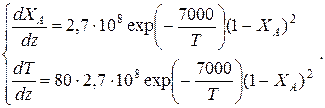
Таблица 9.6. Результаты решения дифференциального уравнения
| z, м | 0,0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,3 |
| XA, % | 0,00 | 12,94 | 30,31 | 51,50 | 70,54 | 82,22 | 88,32 | 90,21 |
| T, K | 350,0 | 360,4 | 372,2 | 391,2 | 406,4 | 415,8 | 420,7 | 422,2 |
Решая полученную систему численным методом, можем найти длину реактора. Например, при решении модифицированным методом Эйлера при шаге интегрирования 0.02 м получаем длину реактора 1,3 м (см.
табл. 9.6).
