Перевод числа из десятичной системы счисления в двоичную (1-й способ). Этот способ перехода от записи числа в десятичною системе счисления к записи его в двоичной системе состоит в представлении числа в виде суммы степеней двойки и последующем выделении коэффициентов такого представления. Продемонстрируем этот способ на примерах:
А) 2710 = (1· 24 + 1· 23 +0· 22 +1· 21 +1· 20)10 =110112
В) 12,2510 = (8 + 4+ 1/4)10 = (23 + 22 + 2-2)10 =
= (1· 23 + 1· 22 + 0· 21 + 0· 20 + 0· 2-1 + 1· 2-2)10 = 1100,012.
2-й способ:
Перевод целых чисел. Пусть требуется найти представление числа 1210 в двоичной системе счисления.
Поступаем следующим образом: делим, начиная с 12, каждое получающееся частное на основание системы, в которую переводим число, то есть на 2. Получаем:
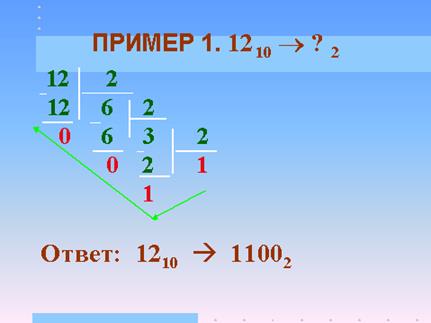
Затем в направлении, указанном стрелкой, начиная с последнего частного (в нашем случае оно всегда будет равно 1), записываемого в старший разряд формируемого двоичного представления, фиксируем все остатки. В итоге получаем ответ: 1210= 11002.
Оба способа правильны и допустимы. Поэтому мы вправе выбрать его по своему усмотрению.
Перевод числа из двоичной системы счисления в десятичную. Это перевод – как бы обратный к изложенному выше. Его наиболее просто осуществить, основываясь на позиционности двоичной системы счисления. Уже отмечалась правомерность записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы:
1012=(1· 22 +0· 21 + 1· 20)10=(4+1)10=510
11012=(1· 23 + 1· 22 + 0· 21 + 1· 20)10 = (8+4)10=1210
1000001001,1012 = (1· 29 + 0· 28 + 0· 27 + 0· 26 + 0· 25+ 0· 24 + 1· 23 + 0· 22 + 0· 21 + 1· 20 1· 2-1 + 0· 2-2 +1· 2-3)10 = (512 + 8 + 1 + 1/2 + 1/8)10 = (521+5/8)10 = (521,625)10
(Заметим, что, несмотря на длину исходной двоичной записи, степени числа 2 легко подсчитываются без калькулятора, которого может не оказаться под рукой.)
Действительно, известно, что
20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, 27=128,
28 = 256, 29=512, 210 = 1024.
Позиционная систе́ма счисле́ния — система счисления, в которой один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
Любое число C в позиционной системе счисления с основанием Р может быть представлено в виде полинома:
C= Cn Pn +Cn-1 Pn-1 +…+C1 P1 +C0 P0 +C-1 P-1 +…+C-m P-m,
 |
или
где в качестве Ci могут стоять любые из Р цифр алфавита, а нижние индексы определяют местоположение цифры в числе (разряд):
* положительные значения индексов - для целой части числа (n разрядов);
* отрицательные значения - для дробной (m разрядов).
В вычислительных системах применяются две формы представления чисел:
· естественная форма, или форма с фиксированной запятой (точкой);
· нормальная форма, или форма с плавающей запятой (точкой).
С фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
C = Cn Cn-1 …C1 C0, C-1… C-m
Запятая опускается, если дробная часть отсутствует. Позиции цифр в такой записи называются разрядами. Разряды нумеруются влево от запятой, начиная с нуля: 0-й,1-й,...(n-1)-й, n-й; и вправо от запятой: 1-й, 2-й,...(m-й).
Значение Ci цифры ci в позиционных системах счисления определяется номером разряда:
Ci = сi Рi.
Величина Pi называется весом, или значением, i-го разряда. В позиционных системах счисления значения соседних разрядов отличаются в P раз: левый в P раз больше правого.
Пример 3.1. Десятичная система счисления.
Р=10.
Цифры: 0,1,2,3,4,5,6,7,8,9.
723,1910 =7×102 +2×101 +3×100 +1×10-1 +9×10-2.
Пример 3.2. Двоичная система счисления.
Р=2.
Цифры: 0,1.
101110,1012 = 1×25 +0×24 +1×23 +1×22 +1×21 +0×20 +1×2-1 +0×2-2 +1×2-3
Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема в вычислениях.
Максимальное целое число, которое может быть представлено в n разрядах:
Nmax = Pn -1.
Минимальное значащее (не равное 0) число, которое можно записать в m разрядах дробной части:
Nmin = P-m.
Имея в целой части числа n, а в дробной части m разрядов, можно записать всего Pn+m разных чисел.
Пример 3.3. Двоичная система счисления.
Р = 2.
n = 10, m = 6.
Возможное для представления значение N лежит в пределах:
0,015<N<1024.
Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных ЭВМ естественная форма представления используется как вспомогательная и только для целых чисел.
С плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, а вторая порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок - целым числом. В общем виде число в форме с плавающей запятой может быть представлено так: 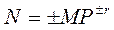 ,
,

где M - мантисса числа (|М| <1);
r - порядок числа (r - целое число);
P - основание системы счисления.






